博客园  :: 首页  :: 新随笔  :: 联系 :: 订阅 订阅  :: 管理

Proximal Policy Optimization(PPO)算法原理介绍学习笔记

Posted on 2023-07-25 00:03  Antel  阅读(3358)  评论(0)  编辑  收藏  举报

在了解PPO之前，首先需要了解Policy Gradient，PPO是建立在PG上的。

Policy Gradient

基本参考【强化学习2】Policy Gradient - LGC的文章 - 知乎进行整理。

给定状态和动作的序列

$s1\rightarrow a1\rightarrow s2 \rightarrow a2\rightarrow ...\rightarrow sT $

记Trajectory为$ \tau={ s1,a1,s2,a2,...,sT,aT }$

则有

\[p_\theta(\tau)=p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)p_\theta(a_2|s_2)p(s_3|s_2,a_2)... =p(s_1)\prod_{t=1}^{T}p_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t) \]

奖励记为

\[R(\tau)=\sum_{t=1}^{T}{r_t} \]

得到奖励的期望

\[\bar{R_\theta}=\sum_{\tau}^{}{R(\tau)p_\theta(\tau)}=E_{\tau\sim p_\theta(\tau)}[R(\tau)] \]

对其求梯度

\[\Delta\bar{R_\theta}=\Delta \sum_{\tau}^{}{R(\tau)p_\theta(\tau)}=\sum_{\tau}^{}{R(\tau)\Delta p_\theta(\tau)} \]

进行一些变换

\[\Delta\bar{R_\theta}=\sum_{\tau}^{}{R(\tau)\Delta p_\theta(\tau)} =\sum_{\tau}^{}{R(\tau)p_\theta(\tau)\Delta p_\theta(\tau)/p_\theta(\tau)} =\sum_{\tau}^{}{R(\tau)p_\theta(\tau)\Delta logp_\theta(\tau)} \]

转化成采样

\[\Delta\bar{R_\theta}=E_{\tau\sim p_\theta(\tau)}[R(\tau)\Delta logp_\theta(\tau)] \approx \frac{1}{N}\sum_{n=1}^{N}{R(\tau^{n})\Delta log(p_\theta(\tau^{n}))} \]

将（1）带入到（6），移除\(\theta\)梯度为0的项，得到

\[\Delta\bar{R_\theta} \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{R(\tau^{n})\Delta log(p_\theta(a_{t}^{n}|s_{t}^{n}))} \]

\(p_\theta(a_{t}^{n}|s_{t}^{n})\)为模型的输出，可以轻松计算梯度

转化成loss

\[loss=min(-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{R(\tau^{n})\log(p_\theta(a_{t}^{n}|s_{t}^{n}))}) \]

其他：

可以对奖励加入一个baseline，保证反馈有正有负

\[\Delta\bar{R_\theta} \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{(R(\tau^{n})-b)\Delta log(p_\theta(a_{t}^{n}|s_{t}^{n}))} \]

可以看到，对于每个action，都有相同的\(R(\tau^{n})-b\)，可以看做是这个动作的权重，但是每个序列的所有动作都有相同的权重看起来并不是特别合理，可以直觉地考虑，每个动作只会对对后续动作产生影响，则权重应该来自于后续的reward。所以修改奖励：

\[\Delta\bar{R_\theta} \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{(\sum_{t'=t}^{T_n}{r_{t'}^{n}}-b)\Delta log(p_\theta(a_{t}^{n}|s_{t}^{n}))} \]

对于每一个action，他对当前奖励影响较大，随着时间推移，这个动作的影响会越来越小，所以应该添加一个修正因子\(\gamma<1\)

\[\Delta\bar{R_\theta} \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{(\sum_{t'=t}^{T_n}{r_{t'}^{n}\gamma^{t'-t}}-b)\Delta log(p_\theta(a_{t}^{n}|s_{t}^{n}))} \]

得到奖励期望的梯度。

由上面可知，

\(loss=-\frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}{R(\tau^{n})\log(p_\theta(a_{t}^{n}|s_{t}^{n}))}\)

\(\log(p_\theta(a_{t}^{n}|s_{t}^{n}))\)对应模型输出token的log_prob，生成的句子的整体reward搭配每个token的log_prob构成了整体loss。

Proximal Policy Optimization（PPO）

基本翻译自https://huggingface.co/learn/deep-rl-course/unit8，稍加整理&自我理解

Actor Critic (A2C)是一种混合结构，包含了基于value和基于policy的方法，包括：

  • Actor：控制agent的行为
  • Critic：度量action的好坏

PPO是一种架构，通过避免policy更新太大，来提升模型训练的稳定性。

维护两个policy，每个policy是AC结构，对旧policy进行动作采样，得到reward等，对新policy进行更新。

采用一个比例表示新旧policy的差别，并将这个比例clip到\([1-\epsilon, 1+\epsilon]\)

Intuition

PPO的主要idea是想在训练时，通过限制对policy的改变来增加训练的稳定性。也就是避免对policy有太大的更新

两个原因：

  • 实验表明，训练时对policy进行更小的更新更可能收敛到最优结果。
  • policy的更新太大容易造成得到不好的policy，loss雪崩，可能导致长时间无法恢复或者不能恢复

PPO中采用更加保守的更新policy的方式、

截断代理目标函数

policy的目标函数，

\(L^{PG}(\theta) = E_t[\log \pi_{\theta}(a_t | s_t) * A_t]\)

其中\(\log \pi_{\theta}(a_t | s_t)\)是某state下的action的log_prob，如果A>0，说明这个action是比其他在这个state的action要好。

PG中计算的梯度可以是对这个目标函数进行梯度计算。

对这个目标函数进行梯度上升时，会推动agent采取能有更好reward的action，避免不好的action。

然后，step的大小引出了些问题：

  • 太小，训练过程过慢
  • 太大：训练时存在太多变化

PPO采用截断代理目标函数的方法得到的新目标函数来更新policy，使用截断的方法限制policy只在小范围中改变。

新函数主要用来避免过大权重更新带来的破坏性后果。

截断代理目标函数：

\(L^{CLIP}(\theta)=\hat{E_t}[\min (r_t(\theta)\hat A_t, clip(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat A_t)]\)

作为之前目标函数的替换，同样可以进行梯度提升。

其中，\(r_t(\theta)\)是比例函数。\(r_t(\theta) = \frac{\pi_\theta (a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\)是在状态\(s_t\)下，当前policy选取\(a_t\)的概率比上之前policy选取\(a_t\)的概率。

可以看到，\(r_t(\theta)\)表示当前和之前policy的概率比例：

  • 如果\(r_t(\theta)>1\)，\(s_t\)时的\(a_t\)更可能在当前policy中出现
  • 如果\(r_t(\theta)\)介于0和1之间，\(a_t\)更可能在之前policy中出现

所以说这个概率比例是一种评估新旧policy区别的简单方法。

截断代理目标函数中的未截断部分\(r_t(\theta)\hat A_t\)，这个比例替换了掉代理目标函数的log_prob，

这提供了新目变函数的左侧部分，令A乘比例。

\(L^{CPI}(\theta)=\hat E_t [\frac{\pi_\theta (a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat A_t] = \hat E_t [r_t(\theta) \hat A_t]\)

如果只看这样的话，那就缺少了一些限制，如果action在当前policy中远比之前policy中更可能出现，将会引入一个很大的梯度step，所以会让policy更新过大。

所以，需要对远离1的比例添加惩罚项，

在进行惩罚时，有两种方案吧：

  • TRPO（Trust Region Policy Optimization）在目标函数外使用KL散度来限制policy更新。但该方法实现复杂，计算时间长。
  • PPO，使用截断代理目标函数直接裁剪目标函数的概率。

在这里，对比率进行截断，

\(L^{CLIP}(\theta)=\hat{E_t}[\min (r_t(\theta)\hat A_t, clip(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat A_t)]\)

因此，因为当前policy不会与之前的有太大变化，保证了不会有太大的policy更新。

\(r_t(\theta)\)被截断到\([1-\epsilon, 1+\epsilon]\)之间。

截断代理目标函数里面有两个概率比例，一个是没被截断的，一个是被截断到\([1-\epsilon, 1+\epsilon]\)之间的，\(\epsilon\)是一个超参数，用了定义阶段区间，论文中定义\(\epsilon=0.2\)

然后采用截断和未截断的取小，所以最终目标是未截断目标的下界。

从截断和未截断中取小意味着我们会根据比例和advantage来选择截断或者未截断。

advantage为正时，期待有更大的\(r_t\)，但会被\(1+\epsilon\)截断

advantage为负时，期待有更小的\(r_t\)，但会被\(1-\epsilon\)截断，不能小得很放肆

截断代理目标函数可视化

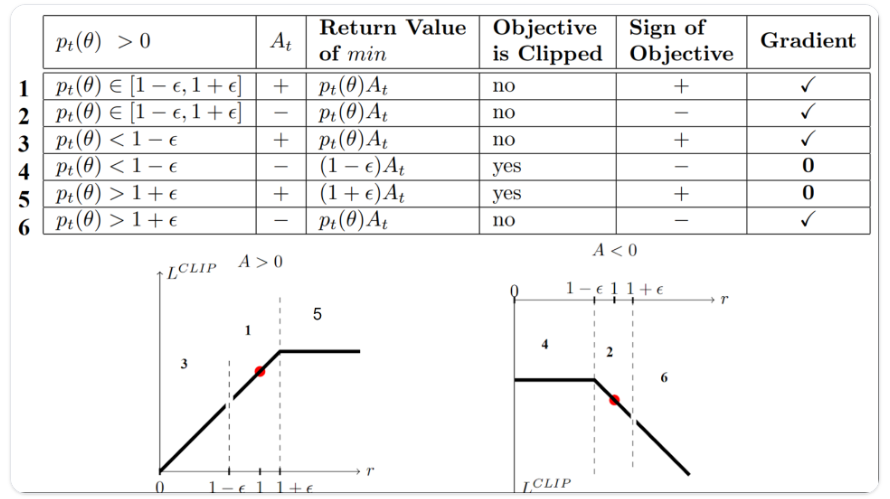
image

图片来源

根据截断和不截断取小，有6种情况。

case1&2 比例在范围区间内

未发生截断，因为比例在\([1-\epsilon, 1+\epsilon]\)之间。

在1中，advantage为正，action比在这个state下的action平均值要好。因此，需要鼓励policy增加state选择这个action的概率。

在2中，advantage为负，action比在这个state下的action平均值要差。因此，需要让policy减少这个state选择这个action的概率。

这两个变化都不大，都无需截断。

case3&4, 比例低于范围区间

如果概率比例低于[1−ϵ]，这个state选择这个action的概率会比之前policy下低很多。

在3中，advantage为正，希望增加action的概率，也没增加多少。

在4中，advantage为负，希望新的policy更少选择这个action，\(r_t(\theta)\hat A_t > clip(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat A_t\)，已经比以前小了，但也打算小不了太少，截断成\(1-\epsilon\)，此时梯度为0

case5&6，比例高于范围区间

这个state选择这个action的概率会比之前policy下高很多。

在5中，advantage为正，但不想要太多，已经比之前policy选这个action的概率要高了。因此，进行截断，梯度为0.

在6中，advantage为负，打算减少这个action的概率。

综上，只在未产生截断的部分进行对policy的更新。当取小的值是截断目标部分，不会更新\(\theta\)因为梯度是0.

所以，需要更新policy的场景有：

  • 比例在\([1-\epsilon, 1+\epsilon]\)之间
  • 比例在区间之外，但是advantage会让选择更靠近合适区间：
    • 低于范围区间但是advantage大于0
    • 高于范围区间但是advantage小于0

关于产生截断时梯度为0的解释：因为比例被截断时，此时的导数不会是\(r_t(\theta)*A_t\)的导数，而是\((1-\epsilon)*A_t\)或者\((1+\epsilon)*A_t\)对\(\theta\)的导数，这两部分都是0。

总的来说，根据截断代理目标，限制了当前policy从之前policy能改变的范围。超过范围的梯度就是0，避免事态严重化。

最终的PPO AC截断代理目标函数如下，包含了截断代理目标函数、价值函数、entropy bonus。

\[L^{CLIP+VF+S}_t(\theta)=\hat E_t [L_t^{CLIP}(\theta) - c_1L_t^{VF}(\theta) + c_2S[\pi_\theta](s_t)] \]

其中，\(c1\)和\(c2\)是系数，\(L_t^{VF}(\theta)\)是平方误差价值函数\((V_\theta(S_t)-V_{+}^{targ})^2\)，用作训练critc模型，令预测值接近reward

\(S[\pi_\theta](s_t)\)是entropy bonus，也就是打算让policy选择的action的entropy变大，这样会保证模型产生足够的探索。

参考

https://huggingface.co/learn/deep-rl-course/unit8

[细(戏)说]RLHF场景下的PPO算法的来龙去脉 - 小神弟弟的文章 - 知乎 https://zhuanlan.zhihu.com/p/631338315

【强化学习2】Policy Gradient - LGC的文章 - 知乎 https://zhuanlan.zhihu.com/p/66205274

【深度强化学习】信任域策略优化：从TRPO到PPO - XuanAxuan的文章 - 知乎 https://zhuanlan.zhihu.com/p/440451849