A Geeky Game Idea
2012.8.31 4th Edition
2012.8.28 3rd Edition
2011.4.28 2nd Edition
2011.3.10 created
萦绕在脑子已久的geek游戏想法。兴趣才是好的老师,要让大家接触到数学的乐趣才能学好数学。
I've always been thinking about making a geeky math game. Interest is the best teacher, if we can make people have fun with math we can make them good at it, especially for American dudes, lol.
1.Background
整个理念就是围绕数学,而手段就是通过图形。举几个例子:
The main idea is about math, the main mechanism is thru graphics. For example:
分型几何其实非常有用,我在大四的时候看过一本书分型几何的书,感悟颇深。比如闪电、山脉、河流、海岸线,都是分型。而所谓无规则布朗运动,并非所谓无规则,可以用分型构造的。(其实有一个问题就是到底什么是规则?人类有限的感官认为规则?永远不要用有限的视野来揣测自然的规则)
Fractal Geometry is kind of important, I remember the last year when I was in college I borrowed a book The Fractal Geometry of Nature , I was really impressed. Stuff like lightning, maintains, river, coastlines, they are all fractions. Our so called irregular motions or Brownian motion, they are not actually without any rules or order, they can be represented by fraction.(Here comes a question, what exactly is regular? things we human beings can perceive and summarize? don't try to think as if you are the god)
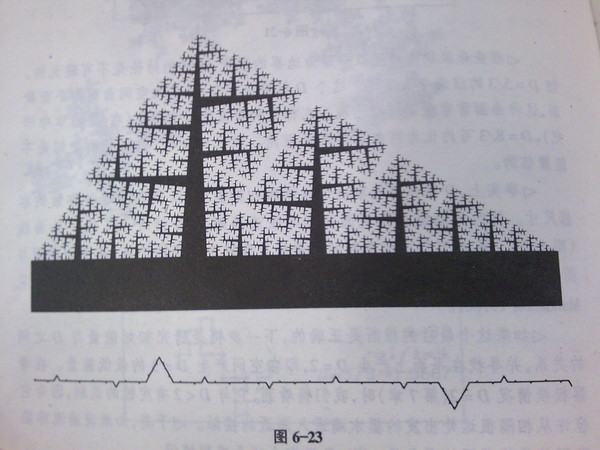
扯远了,举个例子,比如森林的场景可以通过分型几何算出来
Alright, another examples, trees n forests...




云彩,柏林噪声
cloud, Perlin Noise

而海洋河流,可以用sin/cos叠加,事实上在CG领域也是这么做的的。或者也可以用分型构造,
比如The Great Wave off Kanagawa(Hokusai's most famous print, the first in the series 36 Views of Mount Fuji)
高中的时候,班主任薛老师(数学老师,陕西省十大杰出青年)让我们搞了费伯纳切研究性学习,现在想来感触颇深。什么螺旋啊,向日葵啊,自然对数e, 都符合它的规律。。而且和黄金分割也有关系。
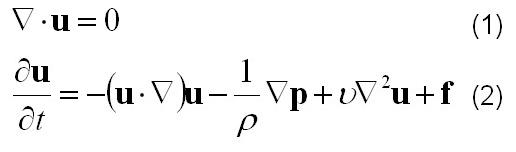
火焰甚至流体,都可以用Navier-Stokes建模,参见我之前的一个帖子..
To model fluids, we can leverage the Navier-Stokes equation, see my post earlier..
http://www.cnblogs.com/antai/archive/2009/12/17/1626157.html
2.Game genre
RPG+Puzzle Solving
3.BrainStorming
比如说第一关,你的敌人是”正整数型“的敌人,如果他接触到你而你比他小,你会死掉。而此时你的技能只有加法和减法,你需要捡起一个”减“血的飞镖丢过去,当他比你小的时候可以吃了他。
比如还有不可约分的分数型敌人,分子分母都是整数,当你用飞镖改变分子分母的值的时候,他可能突变,比如1/3,你扔了一个*30的飞镖给分子,它就图变成了整形的10。
而当你学会了“求导”技能的时候,就可以无视所有的常数敌人。
当学会“积分”的时候,整个屏幕的中立单位都可以按照设定进行积分,然后类似一个陨石砸下来!
当遇到障碍的时候,比如说一个一元一次方程,NPC被困在X里面,可以用“约分“求解,用刀把方程两边劈掉。。也可以”迭代“求解,类似搬箱子,搬来搬去,一直到一个可以接受的解。
在比如学会了防御技能,可以自己设定不同的曲线做为铠甲,比如简单的圆形,多边形,甚至心形曲线、螺旋线。。
游戏分不同的世界,第一世界是正数世界(小学阶段的知识),第二世界是有理数了(中学),第三世界有初等微积分(高中)。。。(最终就是专家模式了,NP问题支持程序内嵌编程的)
boss 在每个世界是不一样的,(注:难度和先后顺序不代表数学家的伟大程度)比如遇到牛顿,这个哥们会“吸引“”积分“什么的,遇到傅立叶会把你属性”变换“什 么的,拉格朗日,欧拉,斯托克斯,费马的。遇到了空间几何怪,你在他法向量上就得费血;而你的矢量箭和中立单位的法向量叉乘,攻击其他角度的敌 人。。
比如到了几何世界,需要自己定义桥的坐标位置、形状。而三维世界需要给敌人,丢过去一个矩阵。有的特定关卡,需要使用”投影“, 然后自定义”光源“,这样让投影通过。。。。
4.展望
也就是说解迷的方法完全根据个人对数学的感悟和理解,而数字和敌人本身是随机产生的,在保证可解的情况下,这个游戏可以无限的玩下去。
请大家多提意见多指正,尤其是关于角色和boss设定。



