分类与回归的区别
Chevalier Meirtz的总结如下:

如何区分类与回归,看的不是输入,而是输出的连续与否。例如:云青青兮欲雨。这个“云青青”就是输入,“青青”就是云的特征,而雨就是我们的预测输出。可以看到,在这个问题中,我们想得到的输出是天气,他是晴朗、阴天等天气状况的子集,是不连续的,所以这就是一个典型的分类问题。
有一个新手特别容易犯的错误就是,认为logistic回归属于回归。但是,
logistic回归不是回归是分类
logistic回归只是用到了回归算法,但是其输出的结果是决策边界,是不连续的。不管是学习ML,数据分析还是数模,这都是一个认识上的误区。评论有小伙伴说Logistic回归过程和线性回归雷同,在二分类问题中,仅仅只是多了一个“阈值判断”,所以应该是回归。但是,Logistc回归仅仅只是过程和线性回归一样,可以归类为GLM,可我们所要讨论的回归和分类,是仅仅对于输出而言的:就像你不能因为用于图像分类的卷积神经网络可以把最后的输出神经元数量换成1、将Softmax去掉并把loss换成MSE后能做回归,那么这样的用于分类的网络就应该是回归一样;在很大程度上,我们甚至可以认为分类和回归就只有是否存在“阈值判断”这么一点区别(多分类就是Softmax吧)。而且中文翻译成“逻辑回归”,也是很不准确的。大牛周志华将其翻译为对数几率回归,因为logistic回归中用到了sigmoid函数,这个翻译是很靠谱的。
分类问题的目的在于寻找决策边界。举个例子,小时候再看电视剧的时候,总喜欢问家长:“这个人是好人还是坏人啊?”而家长心有就有一个评判的标准,好人坏人界限分明,非黑即白;而这个界限,就是决策边界。
----------------------------
其他的回答如下:
分类和回归的区别在于输出变量的类型。
定量输出称为回归,或者说是连续变量预测;
定性输出称为分类,或者说是离散变量预测。
举个例子:
预测明天的气温是多少度,这是一个回归任务;
预测明天是阴、晴还是雨,就是一个分类任务。
--------
主要是loss function不同吧,分类的损失函数一般用交叉熵这种,而回归的损失函数一般用类似 平方误差这种
-------
铁 哥:在说分类与回归的区别之前,先说下分类与回归的相同之处:都属于“监督学习(supervised learning)”,从数学的角度来说,监督学习是一个映射,它存在输入空间和输出空间,分别对应机器学习里常说的样本和标记。
说到这来,就可以开始说分类和回归的区别了:如果标记是离散值,则你面对的是一个分类问题,而如果标记是连续值,则你面对的是一个回归问题。
这就是分类问题和回归问题的区别所在,仅仅通过判断输出值是离散的还是连续的就可以确定;
---------
若我们欲预测的是离散值,例如"好瓜""坏瓜",此类学习任务称为 "分类"。
若欲预测的是连续值,例如西瓜的成熟度0.95 ,0.37,此类学习任务称为"回归"。
陶韬:
链接:https://www.zhihu.com/question/21329754/answer/204957456
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
为什么那么多回答说分类与回归的区别就是离散和连续的区别?
根本不是这样子的啊!
这两者的区别完全不在于连续与否啊,而在于损失函数的形式不同啊!(后文详述)
-------------分割线----------------
前面的很多答案用到了不少生动的例子和理论,从多个角度深刻诠释了什么是分类问题,什么是回归问题,以及如何实现回归与分类任务,但大多数的回答仍没有提及这两者间的本质区别。
个人认为:
“回归与分类的根本区别在于输出空间是否为一个度量空间。”
我们不难看到,回归问题与分类问题本质上都是要建立映射关系:
而两者的区别则在于:
- 对于回归问题,其输出空间B是一个度量空间,即所谓“定量”。也就是说,回归问题的输出空间定义了一个度量
去衡量输出值与真实值之间的“误差大小”。例如:预测一瓶700毫升的可乐的价格(真实价格为5元)为6元时,误差为1;预测其为7元时,误差为2。这两个预测结果是不一样的,是有度量定义来衡量这种“不一样”的。(于是有了均方误差这类误差函数)。
- 对于分类问题,其输出空间B不是度量空间,即所谓“定性”。也就是说,在分类问题中,只有分类“正确”与“错误”之分,至于错误时是将Class 5分到Class 6,还是Class 7,并没有区别,都是在error counter上+1。
而非很多回答所提到的“连续即回归,离散即分类”。
事实上,在实际操作中,我们确实常常将回归问题和分类问题互相转化(分类问题回归化:逻辑回归;回归问题分类化:年龄预测问题——>年龄段分类问题),但这都是为了处理实际问题时的方便之举,背后损失的是数学上的严谨性。
-------------
1、回归问题的应用场景
回归问题通常是用来预测一个值,如预测房价、未来的天气情况等等,例如一个产品的实际价格为500元,通过回归分析预测值为499元,我们认为这是一个比较好的回归分析。一个比较常见的回归算法是线性回归算法(LR)。另外,回归分析用在神经网络上,其最上层是不需要加上softmax函数的,而是直接对前一层累加即可。回归是对真实值的一种逼近预测。
2、分类问题的应用场景
分类问题是用于将事物打上一个标签,通常结果为离散值。例如判断一幅图片上的动物是一只猫还是一只狗,分类通常是建立在回归之上,分类的最后一层通常要使用softmax函数进行判断其所属类别。分类并没有逼近的概念,最终正确结果只有一个,错误的就是错误的,不会有相近的概念。最常见的分类方法是逻辑回归,或者叫逻辑分类。
3、如何选择模型
下面一幅图可以告诉实际应用中我们如何选择合适的模型。
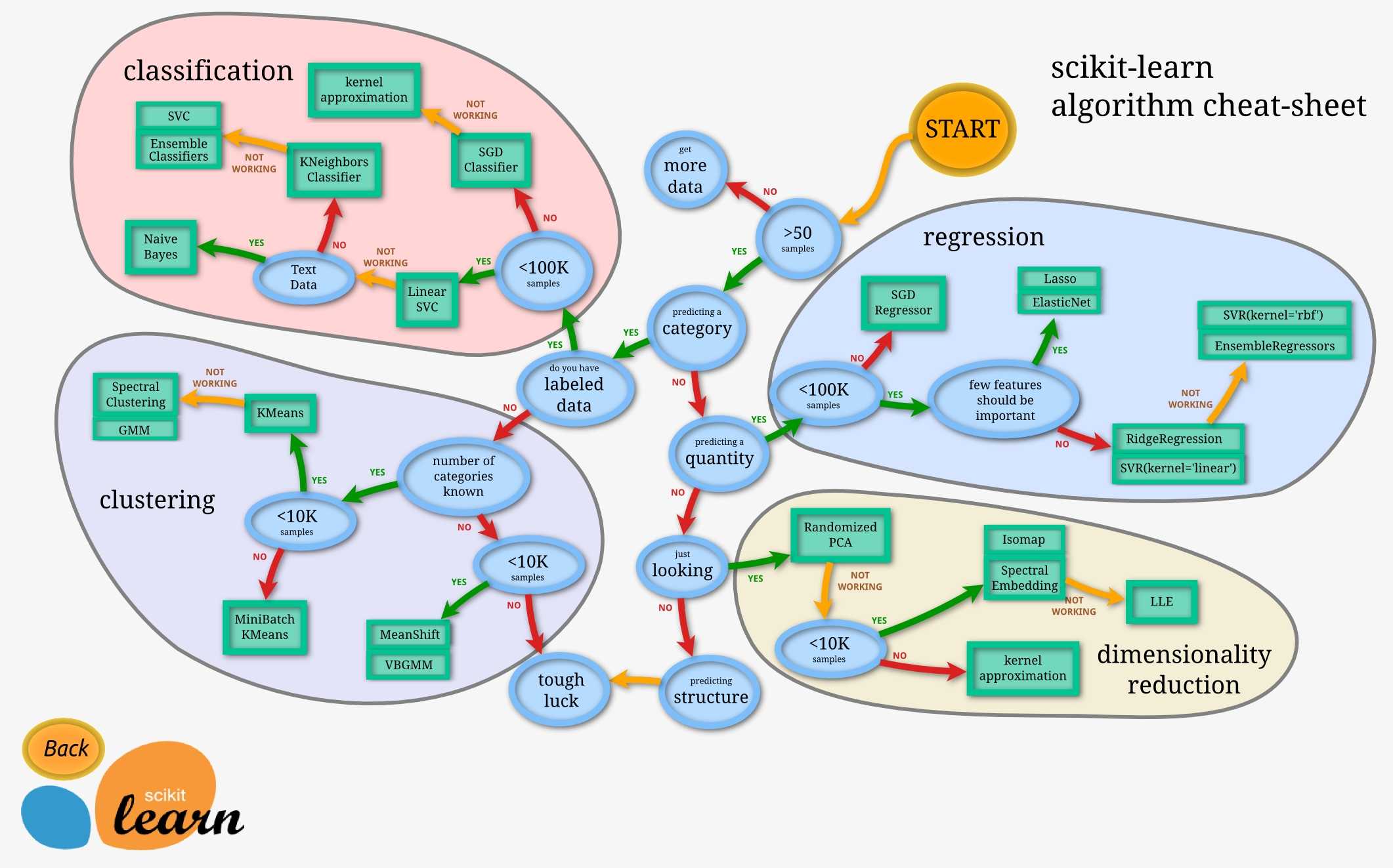
参考资料:



