numpy学习（随机数生成）

numpy.random模块对Python内置的random进行了补充，增加了一些用于高效生成多种概率分布的样本值的函数。例如，你可以用normal来得到一个标准正态分布的4×4样本数组：

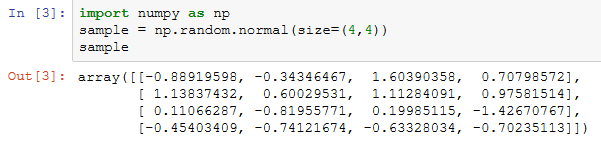
而Python内置的random模块则只能一次生成一个样本值。从下面的测试结果中可以看出，如果需要产生大量样本值，numpy.random快了不止一个数量级：

表4-8列出了numpy.random中的部分函数。

 

随机漫步

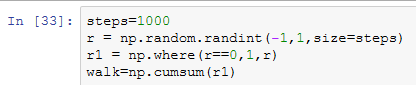
我们通过模拟随机漫步来说明如何运用数组运算。先来看一个简单的随机漫步的例子：从0开始，步长1和－1出现的概率相等。我们通过内置的random模块以纯Python的方式实现1000步的随机漫步：

每次结果肯定不一致，此例中如果是向两个方向运动，则向某个方向移动了60步。

不难看出，这其实就是随机漫步中各步的累计和。用np.random模块一次性随机产生1000个“掷硬币”结果（即两个数中任选一个），将其分别设置为1或－1，然后计算累计和：

有了这些数据之后，我们就可以做一些统计工作了，比如求取最大值、最小值

假设我们想要知道本次随机漫步需要多久才能距离初始0点至少10步远（任一方向均可）。np.abs(walk)>=10可以得到一个布尔型数组，它表示的是距离是否达到或超过10：

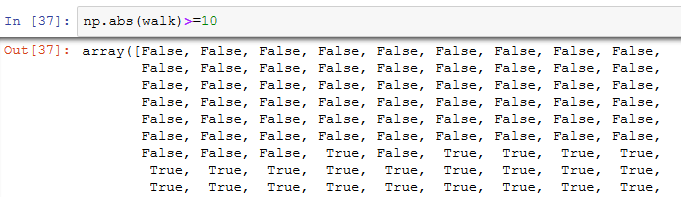
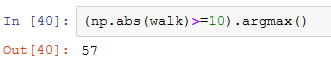
而我们想要知道的是第一个10或－10的索引。可以用argmax来解决这个问题，它返回的是该布尔型数组第一个最大值的索引（True就是最大值）：

这里使用argmax并不是很高效，因为它无论如何都会对数组进行完全扫描。在本例中，只要发现了一个True，那我们就知道它是个最大值了。

 

一次模拟多个随机漫步

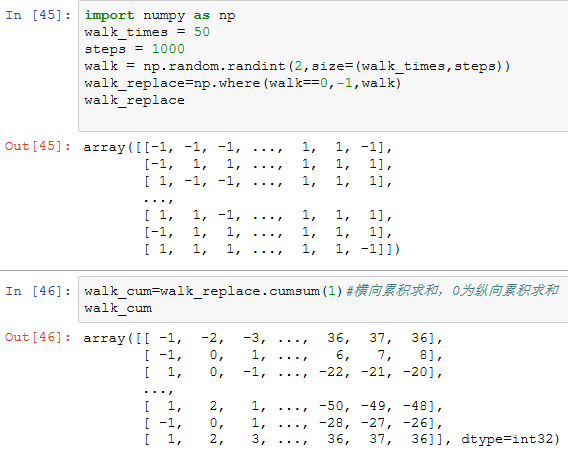
如果你希望模拟多个随机漫步过程（比如5个，当然可以更多如5000个），只需对上面的代码做一点点修改即可生成所有的随机漫步过程。只要给numpy.random的函数传入一个二元元组就可以产生一个二维数组，然后我们就可以一次性计算5随机漫步过程（一行一个）的累计和了：

1轴：对于二维数组的shape（x,y)，即x（行）横向

0轴：对于二维数组的shape(x,y)，即y（列)纵向

 

现在，我们来计算所有随机漫步过程的最大值和最小值：

得到这些数据之后，我们来计算50或－50的最小穿越时间。这里得要稍微动一下脑筋，因为不一定50个过程都到达了50。我们可以用any方法来对此进行检查：

1：横向判断，x=50，即有50个结果：

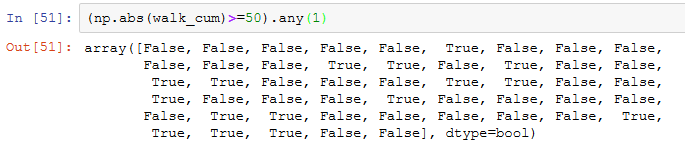
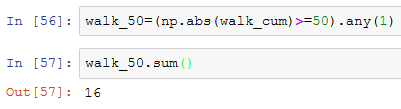
通过计算，50次模拟中16次向某个方向超过50步，上式中求和实际是对True求和，对True进行计算实则是将True看作数字1！

调用argmax在轴1上获取穿越时间：

walk_cum[walk_50]：调用了walk_cum数组中为TRUE的元素组

argmax：1轴上元素为TRUE的下标，（只列出最靠前的第1个）

 

该例也可使用不同的随机数生成函数即如normal用于生成指定均值和标准差的正态分布数据：

In[235]:steps=np.random.normal(loc=0,scale=0.25,.size=(walk_times,steps)