AlgorithmsI Programming Assignment 1: Percolation

 

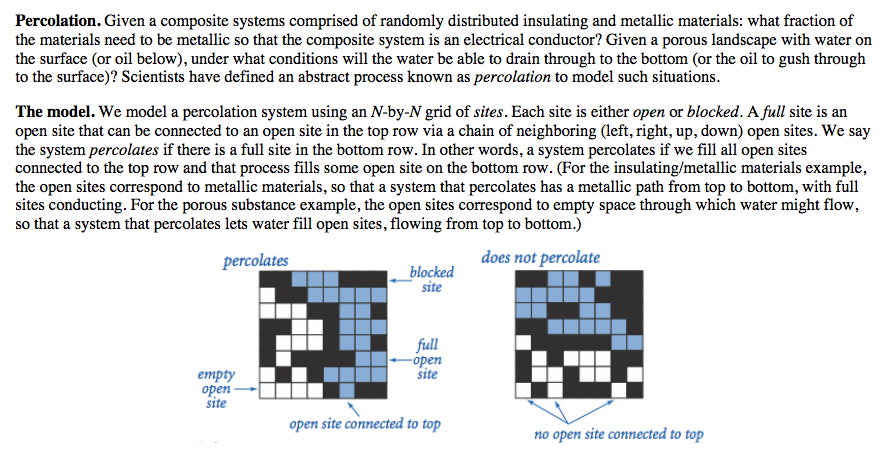
3种版本的答案，第一种使用virtual top and bottom site, 但有backwash的问题，解决这个问题有两种方法：

1. 使用2个WQUUF, 但会增加memory. One for checking if the system percolates(include virtual top and bottom), and the other to check if a given cell is full(only include virtual top). 而且要注意，判断site 是否open只能用boolean ,不然memory 就会超出限制。记住：选择合适的data structure 很重要！！

2. 仍然使用1个WQUUF, 但不使用virtual top and bottom site, 增加判断connect to top 和connect to bottom, 如果出现site 既connect to top 也connect to bottom, 那么percolate.

I found a solution that works really well, that helped me to get bonus points. The general idea is to use only one WQUUF (N*N) and an array (N*N) that contains info about site status. 

We create ONE WQUUF object of size N * N, and allocate a separate array of size N * N to keep the status of each site: blocked, open, connect to top, connect to bottom. I use bit operation for the status so for each site, it could have combined status like Open and connect to top.

 

The most important operation is open(int i, int j): we need to union the newly opened site (let’s call it site ‘S’) S with the four adjacent neighbor sites if possible. For each possible neighbor site(Let’s call it ‘neighbor’), we first call find(neighbor) to get the root of that connected component, and retrieves the status of that root (Let’s call it ‘status’), next, we do Union(S, neighbor); we do the similar operation for at most 4 times, and we do a 5th find(S) to get the root of the newly (copyright @sigmainfy) generated connected component results from opening the site S, finally we update the status of the new root by combining the old status information into the new root in constant time. I leave the details of how to combine the information to update the the status of the new root to the readers, which would not be hard to think of.

 

For the isFull(int i, int j), we need to find the the root site in the connected component which contains site (i, j) and check the status of the root. 

For the isOpen(int i, int j) we directly return the status.

For percolates(), there is a way to make it constant time even though we do not have virtual top or bottom sites: think about why?

So the most important operation  open(int i, int j) will involve 4 union() and 5 find() API calls.

 

I am working on this but I think I understand it. Don't use virtual sites. Find(p) returns the same value for every p in the same component. For every open, call find(p) on neighbors and note down the status of each of the roots of neighbors. I( use a byte array where 0 is closed ; 1 is open. 2 is connectedness to top; 3 is connected to bottom and 4 is both.)

If any of the neighbors have connected to both set or (at least 1 is connected to top AND atleast 1 is connected to bottom) then set some local flag both to true

If connected to top is true set local flag top to true If connected to bottom is true set local flag bottom to true

Now after the unions with neighbors, find root of (I,j) And set its grid status to both or top or bottom.

If you do set it to both then you can also set a class variable percolatesFlag to true for use in the method percolates.

I haven't finished my implementation but it does seem like this will work.

---

java code

1. 有backwash

import edu.princeton.cs.algs4.WeightedQuickUnionUF;

public class Percolation {
    private boolean[] openSite; //if open is 1 , block 0
    private int N; //create N-by-N grid
    private WeightedQuickUnionUF uf; 
    private int top;
    private int bottom;

    public Percolation(int N)  {             // create N-by-N grid, with all sites blocked
        if (N <= 0) {
            throw new IllegalArgumentException("N must be bigger than 0");
        } 
         this.N = N;
         uf = new WeightedQuickUnionUF(N*N + 2);
         openSite = new boolean[N*N+2];   // 0 top_visual N*N+1 bottom_visual
         top = 0;
         bottom = N*N +1;
         for (int i = 1; i <= N*N; i++) {
             openSite[i] = false;   //initial all sites block
         }        
    }
     
    public void open(int i, int j)  {        // open site (row i, column j) if it is not open already
        validateIJ(i, j); 
        int index = xyTo1D(i, j);
        openSite[index] = true; 
  
        if (i == 1) {
            uf.union(index, top);
        }
        if (!percolates()) {
            if (i == N) {
                uf.union(index, bottom);
            }
        }
        if (i < N && openSite[index+N]) {
             uf.union(index, index+N);
        }
        if (i > 1 && openSite[index-N]) {
             uf.union(index, index-N);
        }
        if (j < N && openSite[index+1]) {
             uf.union(index, index+1);
        }
        if (j > 1 && openSite[index-1]) {
             uf.union(index, index-1);
        }
          
    }
    
    private int xyTo1D(int i, int j) {
        validateIJ(i, j);
        return j + (i-1) * N;
    }
    
    private void validateIJ(int i, int j) {
        if (!(i >= 1 && i <= N && j >= 1 && j <= N)) {
            throw new IndexOutOfBoundsException("Index is not betwwen 1 and N");
        }
    }
    
    public boolean isOpen(int i, int j) {     // is site (row i, column j) open?
        validateIJ(i, j);
        return openSite[xyTo1D(i, j)];
    }
    
    /*A full site is an open site that can be connected to an open site in the top row 
     * via a chain of neighboring (left, right, up, down) open sites. 
    */
    public boolean isFull(int i, int j) {    // is site (row i, column j) full?
        validateIJ(i, j);
        return uf.connected(top, xyTo1D(i, j));
    }
    
    /* Introduce 2 virtual sites (and connections to top and bottom). 
     * Percolates iff virtual top site is connected to virtual bottom site.
     */
    public boolean percolates()  {           // does the system percolate? 
        return uf.connected(top, bottom);
    }
    
    public static void main(String[] args) { // test client (optional)
    }
}

2. 使用2个WQUUF

//use two WQUUF
//One way to fix this is two use two different WQUF.
//One for checking if the system percolates(include virtual top and bottom ), 
//and the other to check if a given cell is full(only include virtual top).

import edu.princeton.cs.algs4.WeightedQuickUnionUF;

public class Percolation {  
    private boolean[] openSite; //if open is true , block false
    private int N; //create N-by-N grid
    private WeightedQuickUnionUF uf; 
    private WeightedQuickUnionUF ufNoBottom; 
    private int top;
    private int bottom;
   
    public Percolation(int N)  {             // create N-by-N grid, with all sites blocked
        if (N <= 0) {
            throw new IllegalArgumentException("N must be bigger than 0");
        } 
         this.N = N;
         uf = new WeightedQuickUnionUF(N*N + 2);
         ufNoBottom = new WeightedQuickUnionUF(N*N + 1);
         openSite = new boolean[N*N+2];   // 0 top_visual N*N+1 bottom_visual
         top = 0;
         bottom = N*N +1;
         for (int i = 1; i <= N*N; i++) {
             openSite[i] = false;   //initial all sites block
         }        
    }
     
    public void open(int i, int j)  {        // open site (row i, column j) if it is not open already
        validateIJ(i, j); 
        int index = xyTo1D(i, j);
        openSite[index] = true; 
  
        if (i == 1) {
            uf.union(index, top);
            ufNoBottom.union(index, top);
        }
        if (!percolates()) {
            if (i == N) {
                uf.union(index, bottom);
            }
        }
        if (i < N && openSite[index+N]) {
             uf.union(index, index+N);
             ufNoBottom.union(index, index+N);
        }
        if (i > 1 && openSite[index-N]) {
             uf.union(index, index-N);
             ufNoBottom.union(index, index-N);
        }
        if (j < N && openSite[index+1]) {
             uf.union(index, index+1);
             ufNoBottom.union(index, index+1);
        }
        if (j > 1 && openSite[index-1]) {
             uf.union(index, index-1);
             ufNoBottom.union(index, index-1);
        }
    }
    
    private int xyTo1D(int i, int j) {
        validateIJ(i, j);
        return j + (i-1) * N;
    }
    
    private void validateIJ(int i, int j) {
        if (!(i >= 1 && i <= N && j >= 1 && j <= N)) {
            throw new IndexOutOfBoundsException("Index is not betwwen 1 and N");
        }
    }
    
    public boolean isOpen(int i, int j) {     // is site (row i, column j) open?
        validateIJ(i, j);
        return openSite[xyTo1D(i, j)];
    }
    
    /*A full site is an open site that can be connected to an open site in the top row 
     * via a chain of neighboring (left, right, up, down) open sites. 
    */
    public boolean isFull(int i, int j) {    // is site (row i, column j) full?
        validateIJ(i, j);
        return ufNoBottom.connected(top, xyTo1D(i, j));
    }
    
    /* Introduce 2 virtual sites (and connections to top and bottom). 
     * Percolates iff virtual top site is connected to virtual bottom site.
     */
    public boolean percolates()  {           // does the system percolate? 
        return uf.connected(top, bottom);
    }
    
    public static void main(String[] args) { // test client (optional)
    }
}

3. 最佳方法，增加flag, 只使用1个WQUUF

//use one WQUUF to avoid backwash
import edu.princeton.cs.algs4.WeightedQuickUnionUF;

public class Percolation {  
    private boolean[] open; //blocked: false, open: true
    private boolean[] connectTop;
    private boolean[] connectBottom;
    private int N; //create N-by-N grid
    private WeightedQuickUnionUF uf; 
    private boolean percolateFlag;
  
    public Percolation(int N)  {             // create N-by-N grid, with all sites blocked
        if (N <= 0) {
            throw new IllegalArgumentException("N must be bigger than 0");
        } 
         this.N = N;
         uf = new WeightedQuickUnionUF(N*N);
         open = new boolean[N*N];  
         connectTop = new boolean[N*N];  
         connectBottom = new boolean[N*N];  
      
         for (int i = 0; i < N*N; i++) {
             open[i] = false;
             connectTop[i] = false;
             connectBottom[i] = false;
         } 
         percolateFlag = false;
    }
     
    public void open(int i, int j)  {        // open site (row i, column j) if it is not open already
        validateIJ(i, j); 
        int index = xyTo1D(i, j);
        open[index] = true;  //open
        boolean top = false;
        boolean bottom = false;
       
        if (i < N && open[index+N]) {
            if (connectTop[uf.find(index+N)] || connectTop[uf.find(index)] ) {   
                 top = true;
            }
            if (connectBottom[uf.find(index+N)] || connectBottom[uf.find(index)] ) {   
                 bottom = true;
            }
             uf.union(index, index+N);
        }
        if (i > 1 && open[index-N]) {
            if (connectTop[uf.find(index-N)] || connectTop[uf.find(index)] ) {   
                 top = true;
            }
            if (connectBottom[uf.find(index-N)] || connectBottom[uf.find(index)] ) {   
                 bottom = true;
            }
             uf.union(index, index-N);
        }
        if (j < N && open[index+1]) {
            if (connectTop[uf.find(index+1)] || connectTop[uf.find(index)] ) {   
                 top = true;
            }
            if (connectBottom[uf.find(index+1)] || connectBottom[uf.find(index)] ) {   
                 bottom = true;
            }
             uf.union(index, index+1);
        }
        if (j > 1 && open[index-1]) {
            if (connectTop[uf.find(index-1)] || connectTop[uf.find(index)] ) {   
                 top = true;
            }
            if (connectBottom[uf.find(index-1)] || connectBottom[uf.find(index)] ) {   
                 bottom = true;
            }
             uf.union(index, index-1);
        }
        if(i == 1) {
            top = true;
        }
        if(i == N){
            bottom = true;
        }
        connectTop[uf.find(index)] = top;
        connectBottom[uf.find(index)] = bottom;
        if( connectTop[uf.find(index)] &&  connectBottom[uf.find(index)]) {
            percolateFlag = true;
        }
    }
    
    private int xyTo1D(int i, int j) {
        validateIJ(i, j);
        return j + (i-1) * N -1;
    }
    
    private void validateIJ(int i, int j) {
        if (!(i >= 1 && i <= N && j >= 1 && j <= N)) {
            throw new IndexOutOfBoundsException("Index is not betwwen 1 and N");
        }
    }
    
    public boolean isOpen(int i, int j) {     // is site (row i, column j) open?
        validateIJ(i, j);
        return open[xyTo1D(i, j)];
    }
    
    /*A full site is an open site that can be connected to an open site in the top row 
     * via a chain of neighboring (left, right, up, down) open sites. 
    */
    public boolean isFull(int i, int j) {    // is site (row i, column j) full?
        validateIJ(i, j);
        return connectTop[uf.find(xyTo1D(i, j))];
    }
    
    /* Introduce 2 virtual sites (and connections to top and bottom). 
     * Percolates iff virtual top site is connected to virtual bottom site.
     */
    public boolean percolates()  {           // does the system percolate? 
        return percolateFlag;
    }
    
    public static void main(String[] args) { // test client (optional)
    }
}

---

Reference:

1. http://tech-wonderland.net/blog/avoid-backwash-in-percolation.html