TensorFlow - 起步（Start）

01 - 基本的神经网络结构

输入端---》神经网络（黑盒）---》输出端

• 输入层：负责接收信息
• 隐藏层：对输入信息的加工处理
• 输出层：计算机对这个输入信息的认知

每一层点开都有它相应的内容，函数和功能。
一般来说, 神经网络(Neural Network)是一连串神经层所组成的把输入进行加工再输出的系统。

神经网络的加工处理：

特征(features)---》神经网络层加工---》代表特征(feature representation)---》神经网络层再次加工---》另一种代表特征......
也就是将一种代表特征转换成另一种代表特征，一次次特征之间的转换，也就是一次次的更有深度的理解。
代表特征通常只有计算机自己能够理解。

 

02 - 数据流图（data flow graphs）

TensorFlow是采用数据流图（data flow graphs）来计算，也就是说TensorFlow图（计算图或数据流图）是一种图数据结构。
首先创建一个数据流图，然后再将数据（以张量(tensor)的形式存在）放在数据流图中计算。
数据在输入层输入，在隐藏层加工处理，在输出层输出。

张量流经图，在每个节点由一个指令操控，一个指令的输出张量通常会变成后续指令的输入张量。

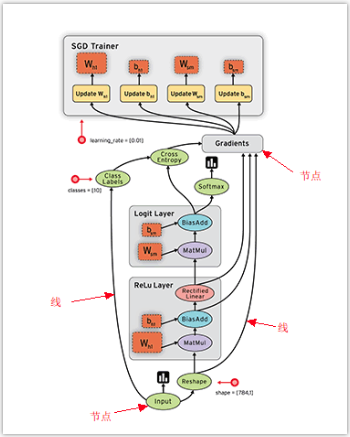
动图：https://www.tensorflow.org/images/tensors_flowing.gif

注意：这里演示图使用了梯度下降处理，梯度下降会对几个参数进行更新和完善，更新后的参数再次跑到隐藏层去学习，这样一直循环，直到结果收敛。

• 图中的节点（Nodes）：表示数学操作，也就是指令
• 图中的线（edges）：表示在节点间相互联系的多维数据数组, 即张量（tensor)

训练模型时tensor会不断的从数据流图中的一个节点flow到另一节点，这就是TensorFlow名字的由来。

TensorFlow仅会根据相关节点的需求在需要时计算节点。

很多TensorFlow程序由单个图构成，但是TensorFlow程序可以选择创建多个图。

TensorFlow编程本质上是一个两步流程：

1.   将常量、变量和指令整合到一个图中。
2.   在一个会话中评估这些常量、变量和指令。

 

03 - 张量（Tensor）

在Tensorflow中，变量统一称作张量（Tensor）。

张量（Tensor）是任意维度的数组。

• 0阶张量：纯量或标量 (scalar)， 也就是一个数值，例如，\'Howdy\' 或 5
• 1阶张量：向量 (vector)或矢量，也就是一维数组（一组有序排列的数），例如，[2, 3, 5, 7, 11] 或 [5]
• 2阶张量：矩阵 (matrix)，也就是二维数组（有序排列的向量），例如，[[3.1, 8.2, 5.9][4.3, -2.7, 6.5]]
• 3阶张量：三维的矩阵，也就是把矩阵有序地叠加起来，成为一个“立方体”
• 以此类推，等等。

在大多数情况下，只会使用一个或多个低维张量（2阶及以下）。

典型 TensorFlow 程序中的大多数代码行都是指令，张量也是计算图中的一种指令。
张量可以作为常量或变量存储在图中。

• 常量是始终会返回同一张量值的指令，存储的是值不会发生更改的张量。
• 变量是会返回分配给它的任何张量的指令，存储的是值会发生更改的张量。 

 

04 - 示例：处理结构

本例简单演示了在TensorFlow中如何用代码来运行搭建的结构：

# coding=utf-8
import tensorflow as tf
import numpy as np  # 使用numpy创建数据
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# ### 创建数据
x_data = np.random.rand(100).astype(np.float32)  # 生成float32类型的100个随机数列
y_data = x_data * 0.1 + 0.3
# print("x_data：\n{} \ny_data：\n{}".format(x_data, y_data))

# ### 创建TensorFlow结构 开始### 
# 搭建模型
Weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0))  # 定义权重变量：1维结构，随机数值范围为“-1.0”到“1.0”
biases = tf.Variable(tf.zeros([1]))  # 定义偏差：初始值定义为0
# print("Weights：{}\nbiases：{}".format(Weights, biases))
y = Weights * x_data + biases  # 预测的y值
# 计算误差
loss = tf.reduce_mean(tf.square(y - y_data))  # 计算误差：计算预测值y和真实值y_data的误差
# 传播误差（反向传递误差，使用优化器减少误差）
optimizer = tf.train.GradientDescentOptimizer(0.5)  # 优化器使用梯度下降法（Gradient Descent）进行参数的更新，学习效率为0.5
train = optimizer.minimize(loss)  # 使用优化器减少误差
# 激活Variable
init = tf.global_variables_initializer()  # 必须初始化所有定义的Variable
# ### 创建TensorFlow结构 结束### 

# ### 训练
with tf.Session() as sess:  # 创建会话
    sess.run(init)  # 用Session来执行init初始化步骤
    for step in range(201):
        sess.run(train)  # 用Session来run每一次training的数据，逐步提升神经网络的预测准确性
        if step % 20 == 0:  # 每隔20次打印Weights和biases
            print("Steps：{} Weights：{} Biases：{}".format(step, sess.run(Weights), sess.run(biases)))

# ### 处理结构
# 在TensorFlow中必须先建立神经网络的结构, 才能放入数据，最终运行这个结构；
# 本例简单演示了在TensorFlow中如何用代码来运行搭建的结构；

 

05 - 示例：会话控制（Session）

# coding=utf-8
import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

matrix1 = tf.constant([[3, 3]])  # 定义一个一行两列的矩阵常量
matrix2 = tf.constant([[2],
                       [2]])  # 定义一个两行一列的矩阵常量
print("matrix1: ", matrix1, "\nmatrix2: ", matrix2, )

product = tf.matmul(matrix1, matrix2)  # 定义矩阵相乘（matrix multiply），但不进行计算

# 使用Session的形式 - 不推荐
sess = tf.Session()  # 注意Session的首字母大写
result = sess.run(product)  # 在Session中激活product并得到计算结果
print("result:", result)
sess.close()  # 关闭session

# 使用Session的形式 - 推荐
with tf.Session() as sess2:
    result2 = sess2.run(product)
    print("result2:", result2)

# ### 会话控制（Session）
# 在TensorFlow中，Session是控制和输出文件的执行语句
# 运行session.run()可以获得运算结果, 或者控制运算

 

06 - 示例：变量（Variable）

# coding=utf-8
import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

state = tf.Variable(6, name='counter')  # 在TensorFlow中变量必须先被定义，变量counter的初始值值为6
print("tf.Variable(6, name='counter')：", state.name, state)

one = tf.constant(1)  # 定义常量one，值为1
print("tf.constant(1)：", one)

new_value = tf.add(state, one)  # 定义加法步骤，但并没有直接计算
print("tf.add(state, one)：", new_value)
update = tf.assign(state, new_value)  # 加载new_value到state
print("tf.assign(state, new_value)：", update)

init = tf.global_variables_initializer()  # 必须初始化变量！

# 演示：在Session中完成变量和常量的相加
with tf.Session() as sess:
    sess.run(init)  # 在Session中激活变量
    for _ in range(3):
        sess.run(update)  # 在Session调用前面定义的update
        # print(state)  # 无法打印出state内容
        print(sess.run(state))  # 需要将Session的指针指向state，才能打印出state内容

# ### 变量（Variable）
# 定义语法： state = tf.Variable()
# 如果定义Variable, 就必须要initialize

 

07 - 示例：传入值（Placeholder）

# coding=utf-8
import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

input1 = tf.placeholder(tf.float32)  # 定义placeholder的type为float32
input2 = tf.placeholder(tf.float32)
output = tf.multiply(input1, input2)  # 将input1和input2做乘法运算（multiply）并输出为 output

with tf.Session() as sess:
    print(sess.run(output, feed_dict={input1: [8], input2: [2]}))  # 需要传入的值放在feed_dict={}，并一一对应每一个input

# ### 传入值（Placeholder）
# placeholder是TensorFlow中的占位符，暂时储存变量；
# 使用tf.placeholder()可以从外部传入data到TensorFlow；
# 传输数据的形式为：“sess.run(***, feed_dict={input: **})”，也就是说通过sess.run()完成传值；

 

08 - 激励函数 (Activation Function，AF)

线性方程 (linear function)与非线性方程 (nonlinear function)

• 线性方程：一种代数方程，这种方程的图形为一直线，所以称为线性方程。
• 非线性方程：因变量与自变量之间的关系不是线性的关系。例如：平方关系、对数关系、指数关系、三角函数关系等等。求解非线性方程往往很难得到精确解，求解的基本方法是迭代法（逐渐接近精确解）。

激活函数 (activation function)

一种函数（例如 ReLU 或 S 型函数），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

引入激励函数是为了解决日常生活中不能用线性方程所概括的问题。
激励函数(AF)其实就是另外一个非线性函数，比如说relu, sigmoid, tanh等，嵌套在原有的线性结果上，使得输出结果也具有了非线性的特征。

可以创造自己的激励函数（必须是可以微分的）来处理自己的问题。
在backpropagation误差反向传递的时，只有可微分的激励函数才能把误差传递回去。

常用选择

如果神经网络层只有两三层，那么对于隐藏层，可以使用任意的激励函数。
如果使用特别多层的神经网络，必须慎重选择激励函数，避免梯度爆炸、梯度消失的问题。

默认首选的激励函数：

• 在少量层结构中, 可以尝试多种不同的激励函数。
• 在卷积神经网络（Convolutional Neural Networks，CNN）的卷积层中, 推荐的激励函数是relu。
• 在循环神经网络（Recurrent Neural Networks，RNN）中，推荐的是tanh或者是relu。

官网信息

Tensorflow提供激励函数（Neural Network - Activation Functions）：https://www.tensorflow.org/api_guides/python/nn