ML - 深度学习之美十四章-概念摘要（1~7）

原文链接：https://yq.aliyun.com/topic/111
本文是对原文内容中部分概念的摘取记录，可能有轻微改动，但不影响原文表达。

---

01 - 一入侯门“深”似海，深度学习深几许

什么是“学习”？

“如果一个系统，能够通过执行某个过程，就此改进了它的性能，那么这个过程就是学习”。
学习的核心目的，就是改善性能。

什么是机器学习？

定义1：
对于计算机系统而言，通过运用数据及某种特定的方法（比如统计的方法或推理的方法），来提升机器系统的性能，就是机器学习。
定义2：
对于某类任务（Task，简称T）和某项性能评价准则（Performance，简称P），如果一个计算机程序在T上，以P作为性能的度量，随着很多经验（Experience，简称E）不断自我完善，那么我们称这个计算机程序在从经验E中学习了。

学习问题的三个特征：

• 任务的类型
• 衡量任务性能提升的标准
• 获取经验的来源

统计机器学习

统计机器学习的对象，其实就是数据。
对于计算机系统而言，所有的“经验”都是以数据的形式存在的。
作为学习的对象，数据的类型是多样的，可以是各种数字、文字、图像、音频、视频，也可以是它们的各种组合。
统计机器学习，就是从数据出发，提取数据的特征，抽象出数据的模型，发现数据中的知识，最后又回到数据的分析与预测当中去。

传统的机器学习方式

传统的机器学习方式，通常是用人类的先验知识，把原始数据预处理成各种特征（feature），然后对特征进行分类。
然而，这种分类的效果，高度取决于特征选取的好坏。
传统的机器学习专家们，把大部分时间都花在如何寻找更加合适的特征上。
因此，传统的机器学习，其实可以有个更合适的称呼：特征工程（feature engineering）。
特征是由人找出来的，自然也就为人所能理解，性能好坏，机器学习专家们可以“冷暖自知”，灵活调整。

深度学习

深度学习在本质上属于可统计不可推理的统计机器学习范畴。
很多时候呈现出来的就是一个黑箱（Black Box）系统，其性能很好，却不知道为何而好，缺乏解释性。
深度学习中的“end-to-end（端到端）：输入的是原始数据（始端），然后输出的直接就是最终目标（末端），中间过程不可知。
深度学习的学习对象同样是数据，但与传统机器学习所不同的是，它需要大量的数据，也就是“大数据（Big Data）”。

深度学习的产生

阶段1：特征表示学习（feature representation learning）

• 神经网络自己学习如何抓取数据的特征
• 效果好，对数据的拟合也更加灵活好用
• 代价：机器自己学习出来的特征存在于机器空间，完全超越了人类理解的范畴，成为了“黑盒”，人们只能依据经验调试神经网络的学习性能，不断地尝试性地进行大量重复的网络参数调整

阶段2：深度学习

• 网络进一步加深，出现了多层次的“表示学习”，学习的性能提升到另一个高度。
• 这种多层次的“表示学习”，人们称之为“Deep Learning（深度学习）”。

机器学习与深度学习的简明对比

“机器学习”的核心要素，那就是通过对数据运用，依据统计或推理的方法，让计算机系统的性能得到提升。
而深度学习，则是把由人工选取对象特征，变更为通过神经网络自己选取特征，为了提升学习的性能，神经网络的表示学习的层次较多（较深）。

---

02 - 人工“碳”索意犹尽，智能“硅”来未可知

深度学习的算法

深度学习是高度数据依赖型的算法，它的性能通常随着数据量的增加而不断增强，也就是说它的可扩展性（Scalability）显著优于传统的机器学习算法。
如果训练数据比较少，深度学习的性能并不见得就比传统机器学习好。
其潜在的原因在于，作为复杂系统代表的深度学习算法，只有数据量足够多，才能通过训练，在深度神经网络中，“恰如其分”地将把蕴含于数据之中的复杂模式表征出来。

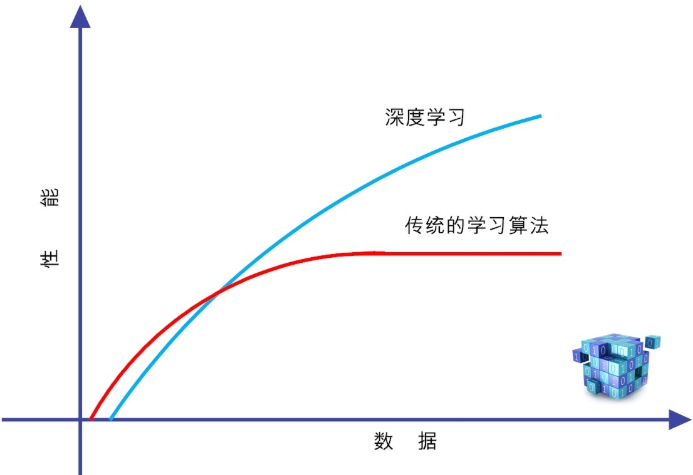
机器学习的两层作用

• （1）面向过去（对收集到的历史数据，用作训练），发现潜藏在数据之下的模式，
  描述性分析（Descriptive Analysis），主要使用了“归纳”。
  对历史对象的归纳，可以让人们获得新洞察、新知识，
• （2）面向未来，基于已经构建的模型，对于新输入数据对象实施预测，
  预测性分析（Predictive Analysis），更侧重于“演绎”。
  对新对象实施演绎和预测，可以使机器更加智能，或者说让机器的某些性能得以提高。

二者相辅相成，均不可或缺。

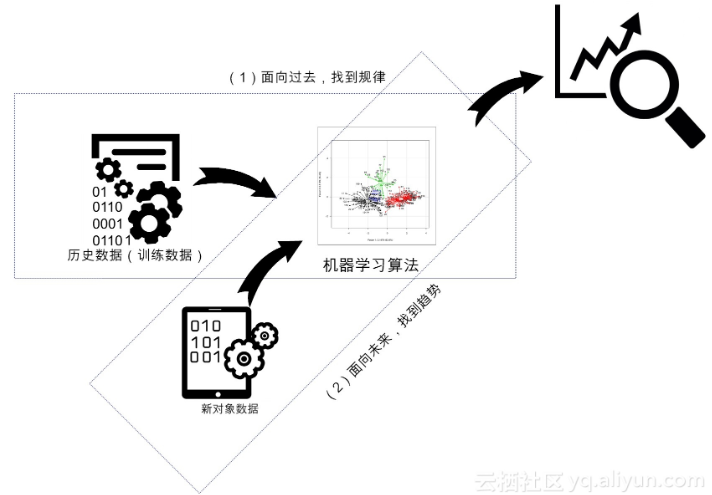
机器学习的三步法

机器学习在本质就是寻找一个好用的函数，具体说来，机器学习要想做得好，需要走好三大步：

• （1）如何找一系列函数来实现预期的功能，这是建模问题。
• （2）如何找出一组合理的评价标准，来评估函数的好坏，这是评价问题。
• （3） 如何快速找到性能最佳的函数，这是优化问题。

什么是神经网络？

“神经网络，是一种由具有自适应性的简单单元构成的广泛并行互联的网络，它的组织结构能够模拟生物神经系统对真实世界所作出的交互反应。”

人工智能领域的两大主流门派

符号主义

• 理念：知识是信息的一种表达形式，人工智能的核心任务，就是处理好知识表示、知识推理和知识运用。
• 核心方法论：自顶向下设计规则，然后通过各种推理，逐步解决问题。

连接主义

• 理念：人的思维就是某些神经元的组合，因此可以在网络层次上模拟人的认知功能，用人脑的并行处理模式，来表征认知过程。
• 核心方法论：试图编写一个通用模型，然后通过数据训练，不断改善模型中的参数，直到输出的结果符合预期。
• 这种受神经科学的启发的网络，被称之人工神经网络（Artificial Neural Network，简称ANN），演化升级后，就是深度学习。

通用近似定理（Universal Approximation Theorem）

只需一个包含足够多神经元的隐藏层，多层前馈网络能以任意精度逼近任意复杂度的连续函数。
换句话说，神经网络可在理论上解决任何问题。

---

03 - 神经网络不胜语， M-P模型似可寻

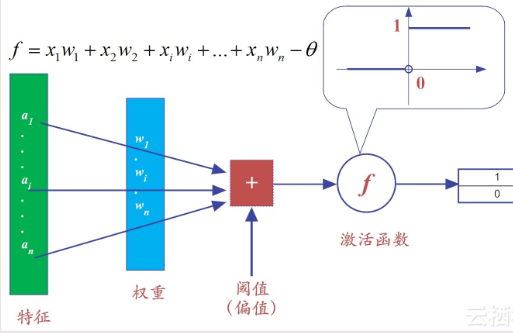
什么是M-P神经元模型？

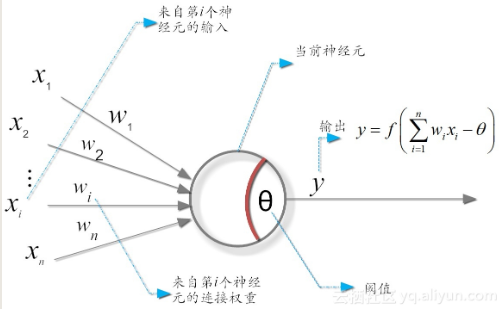
在这个模型中，神经元接收来自n个其它神经元传递过来的输入信号。
这些信号的表达，通常通过神经元之间连接的权重（weight）大小来表示。
神经元将接收到的输入值按照某种权重叠加起来，并将当前神经元的阈值进行比较。
然后通过“激活函数（activation function）”向外表达输出（这在概念上就叫感知机）。

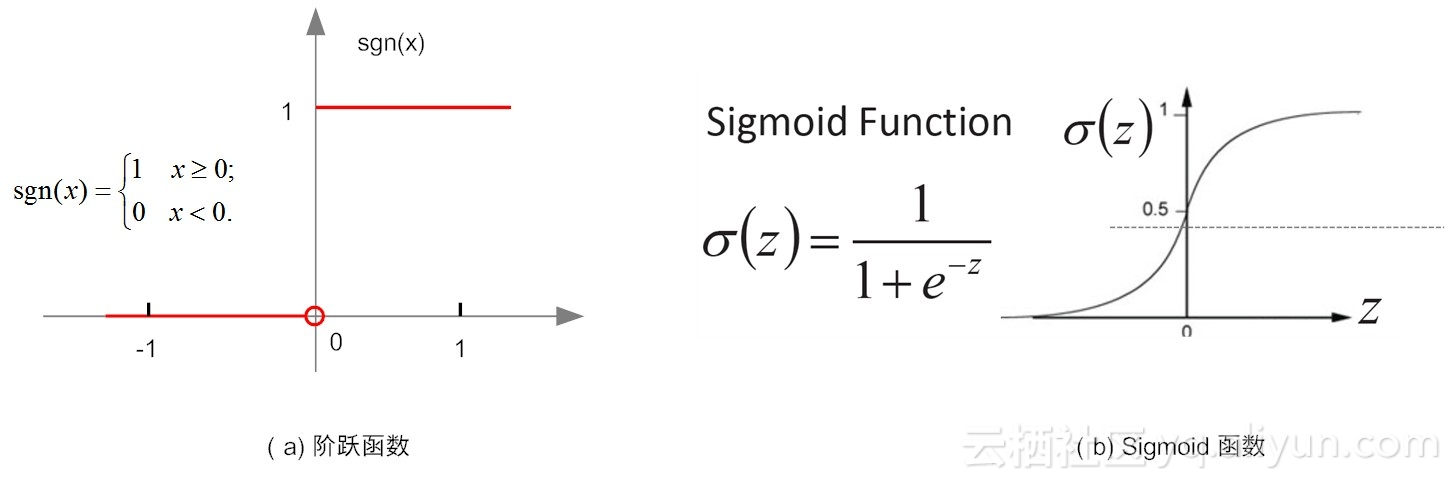
激活函数（activation functions）

在实际使用中，阶跃函数具有不光滑、不连续等众多不“友好”的特性。
为什么说它“不友好”呢，这是因为在训练网络权重时，通常依赖对某个权重求偏导、寻极值，而不光滑、不连续等通常意味着该函数无法“连续可导”。
通常用Sigmoid函数来代替阶跃函数。这个函数可以把较大变化范围内输入值（x）挤压输出在（0,1）范围之内，故此这个函数又称为“挤压函数（Squashing function）”。

激活函数 (activation function)的定义：一种函数（例如 ReLU 或 S 型函数），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

卷积函数（convolutional function）

通俗来讲，所谓卷积，就是一个功能和另一个功能在时间的维度上的“叠加”作用。
假设：

• 时间维度上的函数f
• 操作函数g
• 函数h

如果，“h = f * g”，那么卷积得到的函数h一般要比f和g都光滑。
利用这一性质，对于任意的可积函数f，都可简单地构造出一列逼近于f的光滑函数列，这种方法被称之为函数的光滑化或正则化。
在时间的维度上的“叠加作用”，如果函数是离散的，就用求累积和来刻画。如果函数是连续的，就求积分来表达。

“M-P”感知机模型

简单来说，感知机模型，就是一个由两层神经元构成的网络结构，输入层接收外界的输入，通过激活函数（阈值）变换，把信号传送至输出层。
因此也称之为“阈值逻辑单元（threshold logic unit）”，正是这种简单的逻辑单元，慢慢演进，越来越复杂，就构成了深度学习网络。

---

04 - “机器学习”三重门，“中庸之道”趋若人

机器学习的三种主要形式：监督学习、非监督学习和半监督学习。它们之间核心区别在于是否（部分）使用了标签数据。

监督学习（Supervised Learning）

监督学习基本上就是“分类（classification）”的代名词。
从有标签的训练数据中学习，然后给定某个新数据，预测它的标签（given data, predict labels）。这里的标签（label），其实就是某个事物的分类。
简单来说，监督学习的工作，就是通过有标签的数据训练，获得一个模型，然后通过构建的模型，给新数据添加上特定的标签。
事实上，整个机器学习的目标，都是使学习得到的模型，能很好地适用于“新样本”，而不是仅仅在训练样本上工作得很好。
通过训练得到的模型，适用于新样本的能力，称之为“泛化（generalization）能力”。

非监督学习（Unsupervised Learning）

非监督学习，本质上，就是“聚类（cluster）”的近义词
与监督学习相反的是，非监督学习所处的学习环境，都是非标签的数据。
简单来说，给定数据，从数据中学，能学到什么，就看数据本身具备什么特性了（given data, learn about that data）。
一旦归纳出“类”或“群”的特征，如果再要来一个新数据，就根据它距离哪个“类”或“群”较近，就“预测”它属于哪个“类”或“群”，从而完成新数据的“分类”或“分群”功能。
这里的“类”也好，“群”也罢，事先是不知道的。

半监督学习（Semi-supervised Learning）：

这类学习方式，既用到了标签数据，又用到了非标签数据。
事实上，半监督学习就是以“已知之认知（标签化的分类信息）”，扩大“未知之领域（通过聚类思想将未知事物归类为已知事物）”。
但这里隐含了一个基本假设——“聚类假设（cluster assumption）”，其核心要义就是：“相似的样本，拥有相似的输出”。

---

05 - Hello World感知机，懂你我心才安息

感知机（ Perceptrons ）

基本上来说，感知机是一切神经网络学习的起点，是神经网络学习的“Hello World”。
所谓的感知机，其实就是一个由两层神经元构成的网络结构。
在输入层接收外界的输入，通过激活函数（含阈值）的变换，把信号传送至输出层，因此也称之为“阈值逻辑单元（threshold logic unit）”。
感知机学习属于“有监督学习”（即分类算法）。

这里，使用了最为简单的阶跃函数（step function）。在阶跃函数中，输出规则非常简单：当x>0时，f(x)输出为1，否则输出0。

感知机的学习与训练

所谓神经网络的学习规则，就是调整权值和阈值的规则（这个结论对于深度学习而言，依然是适用的）。

在有监督的学习规则中，需要根据输出与期望值的“落差”，经过多轮重试，反复调整神经网络的权值，直至这个“落差”收敛到能够忍受的范围之内，训练才告结束。
更一般地，当给定训练数据，神经网络中的参数（权值和阈值）都可以通过不断地“纠偏”学习得到。

学习率的作用是“缓和”每一步权值调整强度的。
如果学习率太小，网络调参的次数就太多，从而收敛很慢。
如果学习率太大，会错过了网络的参数的最优解。
本身的大小比较难以确定的，合适的学习率大小，在某种程度上，还依赖于人工经验。

感知机的表征能力

由于感知机只有输出层神经元可以进行激活函数的处理，也就是说它只拥有单层的功能元神经元（functional neuron），因此它的学习能力是相对有限的。
可以解决原子布尔函数中的“与、或、非”等问题都是线性可分的（linearly separable）的问题。
但却连简单的“异或”功能都无法实现。

---

06 - 损失函数减肥用，神经网络调权重

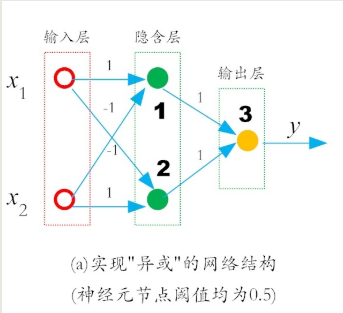
通过多层网络解决“异或”问题

复杂的网络，表征能力就比较强，可以通过多层网络解决“异或”问题。
在输入层和输出层之间，添加一层神经元，将其称之为隐含层（hidden layer，亦有简称为“隐层”）。
这样一来，隐含层和输出层中的神经元都拥有激活函数。
通过设置各个神经元的阈值和权值，就能够实现“异或”功能。

多层前馈神经网络（multi-layer feedforward neural networks

每一层神经元仅仅与下一层的神经元全连接。
而在同一层，神经元彼此不连接，而且跨层的神经元，彼此间也不相连。
这种被简化的神经网络结构，被称之为“多层前馈神经网络”。

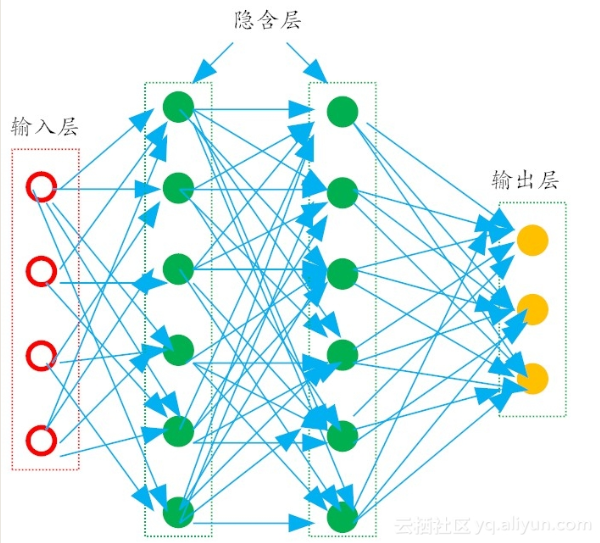
在多层前馈神经网络中，

• 输入层神经元主要用于接收外加的输入信息。
• 在隐含层和输出层中，都有内置的激活函数，可对输入信号进行加工处理。
• 最终的结果，由输出层“呈现”出来。

激活函数可以是阶跃函数、Sigmod函数，还可以是现在深度学习常用的ReLU（Rectified Linear Unit）和sofmax等。

简单来说，神经网络的学习过程，就是通过根据训练数据，来调整神经元之间的连接权值（connection weight）以及每个功能神经元的输出阈值。
连接权值和输出阈值，这是整个神经网络的灵魂所在，需要通过反复训练，方可得到合适的值。
换言之，神经网络需要学习的东西，就蕴含在连接权值和阈值之中。

分布式表征（Distributed Representation）

简单来说，就是当我们表达一个概念时，神经元和概念之间不是一对一对应映射（map）存储的，它们之间的关系是多对多。
具体而言，就是一个概念可以用多个神经元共同定义表达，同时一个神经元也可以参与多个不同概念的表达，只不过所占的权重不同罢了。
分布式表征表示有很多优点。其中最重要的一点，莫过于当部分神经元发生故障时，信息的表达不会出现覆灭性的破坏

损失函数（loss function）

也称为代价函数（cost function）来度量实际输出值和原先预期值二者之间的“落差”程度。
利用损失函数可以反向配置网络中的权值（weight），让损失（loss）最小。
损失函数值越小，说明实际输出和预期输出的差值就越小，也就说明构建的模型越好。
神经网络学习的本质，其实就是利用“损失函数（loss function）”，来调节网络中的权重（weight）。

常见的损失函数

• 0-1损失函数（0-1 loss function）
• 绝对损失函数（absolute loss function）
• 平方损失函数（quadratic loss function）
• 对数损失函数（logarithmic loss function）：便于使用最大似然估计的方法来求极值

反向调节网络参数

两大类方法：

误差反向传播（Error Back propagation，简称BP）
简单说来，就是首先随机设定初值，然后计算当前网络的输出，然后根据网络输出与预期输出之间的差值，采用迭代的算法，反方向地去改变前面各层的参数，直至网络收敛稳定。
BP反向传播算法直接把纠错的运算量，降低到只和神经元数目本身成正比的程度。
但实际用起来它还是有些问题。
比如说，在一个层数较多网络中，当它的残差反向传播到最前面的层（即输入层），其影响已经变得非常之小，甚至出现梯度扩散（gradient-diffusion），严重影响训练精度。

逐层初始化”(layer-wise pre-training)训练机制
当前主流的、“深度学习”常用的方法。
不同于BP的“从后至前”的训练参数方法，“深度学习”采取的是一种从“从前至后”的逐层训练方法。

---

07 - 山重水复疑无路，最快下降问梯度

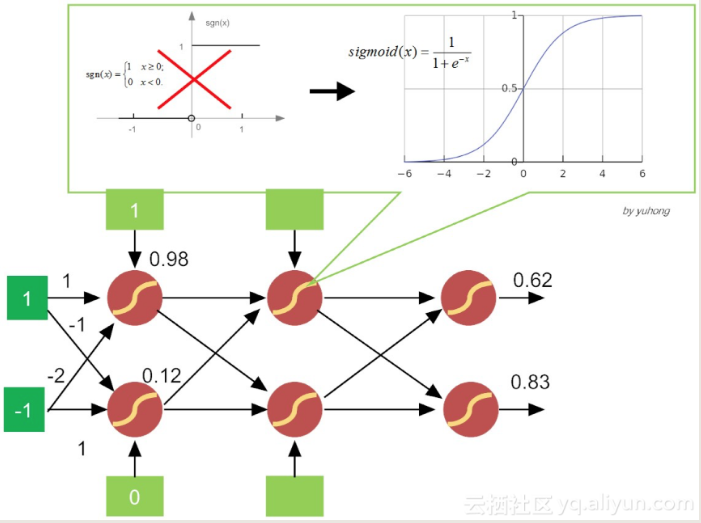
Sigmoid

激活函数从简单粗暴的“阶跃函数”变成了比较平滑的挤压函数Sigmoid。
激活函数为什么要换成Sigmoid呢？
因为感知机的激活函数是阶跃函数，不利于函数求导，进而求损失函数的极小值。
当分类对象是线性可分，且学习率（learning rate）足够小时，由感知机还堪胜任，由其构建的网络，还可以训练达到收敛。
但分类对象不是线性可分时，感知机就有点“黔驴技穷”了。
因此，通常感知机并不能推广到一般前馈网络中。

选择最佳的参数

如何从众多网络参数（神经元之间的链接权值和阈值）中选择最佳的参数呢？
最简单粗暴的方法，当然就是枚举所有可能值了！
但这种暴力调参找最优参数，不适用稍微复杂（层次多、神经元多）的网络，既不优雅，也不高效，故实不可取！

delta法则（delta rule）方法可以让目标收敛到最佳解的近似值。
核心思想在于，使用梯度下降（gradient descent）的方法找极值。
具体说来，就是在假设空间中搜索可能的权值向量，并以“最佳”的姿态，来拟合训练集合中的样本，也就是使损失函数达到最小值！

梯度递减（gradient descent）

也称为梯度下降。
一种通过计算并且减小梯度将损失降至最低的技术，它以训练数据为条件，来计算损失相对于模型参数的梯度。
通俗来说，梯度下降法以迭代方式调整参数，逐渐找到权重和偏差的最佳组合，从而将损失降至最低。

---