机器学习入门16 - 多类别神经网络 (Multi-Class Neural Networks)

原文链接：https://developers.google.com/machine-learning/crash-course/multi-class-neural-networks/

多类别分类，这种模型可从多种可能的情况中进行选择。 

1- 一对多

一对多提供了一种利用二元分类的方法。
鉴于一个分类问题会有 N 个可行的解决方案，一对多解决方案包括 N 个单独的二元分类器，每个可能的结果对应一个二元分类器。
在训练期间，模型会训练一系列二元分类器，使每个分类器都能回答单独的分类问题。
以一张狗狗的照片为例，可能需要训练五个不同的识别器，其中四个将图片看作负样本（不是狗狗），一个将图片看作正样本（是狗狗）。

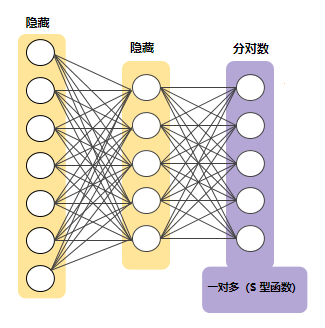
一对多神经网络
当类别总数较少时，这种方法比较合理，但随着类别数量的增加，其效率会变得越来越低下。
此时，可以借助深度神经网络（在该网络中，每个输出节点表示一个不同的类别）创建明显更加高效的一对多模型。
       

2- Softmax

逻辑回归可生成介于 0 和 1.0 之间的小数，Softmax是逻辑回归在多类别问题中的延伸。
也就是说，在多类别问题中，Softmax会为每个类别分配一个用小数表示的概率。
这些用小数表示的概率相加之和必须是“1.0”。
与其他方式相比，这种附加限制有助于让训练过程更快速地收敛。

Softmax层是紧挨着输出层之前的神经网络层，必须和输出层拥有一样的节点数。  
       
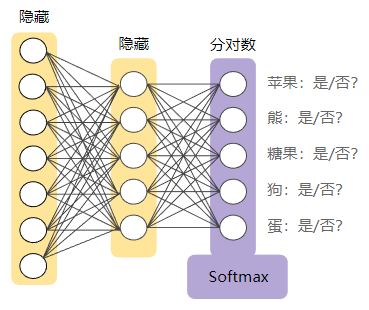
注意：图中每个类别的概率相加之和是“1.0”。
Softmax公式（本质上是将逻辑回归公式延伸到了多类别）：
        $p(y = j|\textbf{x})  = \frac{e^{(\textbf{w}_j^{T}\textbf{x} + b_j)}}{\sum_{k\in K} {e^{(\textbf{w}_k^{T}\textbf{x} + b_k)}} }$

2.1 Softmax 选项

完整 Softmax
    针对每个可能的类别计算概率。
候选采样
    针对所有正类别标签计算概率，但仅针对负类别标签的随机样本计算概率。
    例如，如果想要确定某个输入图片是小猎犬还是寻血猎犬图片，则不必针对每个非狗狗样本提供概率。

类别数量较少时，完整 Softmax 代价很小，但随着类别数量的增加，它的代价会变得极其高昂。
候选采样可以提高处理具有大量类别的问题的效率。 

2.2 一个标签与多个标签

Softmax 假设每个样本只是一个类别的成员。
但是，对于一些样本可以同时是多个类别成员的情况：

• 不能使用 Softmax。
• 必须依赖多个逻辑回归。

例如，假设样本是只包含一项内容（一块水果）的图片。
Softmax 可以确定该内容是梨、橙子、苹果等的概率。
如果样本是包含各种各样内容（几碗不同种类的水果）的图片，必须改用多个逻辑回归。

3- 练习

xxx

4- 关键词

多类别分类 (multi-class classification)
区分两种以上类别的分类问题。
例如，枫树大约有 128 种，因此，确定枫树种类的模型就属于多类别模型。
反之，仅将电子邮件分为两类（“垃圾邮件”和“非垃圾邮件”）的模型属于二元分类模型。

一对多 (one-vs.-all)
假设某个分类问题有 N 种可能的解决方案，一对多解决方案将包含 N 个单独的二元分类器 - 一个二元分类器对应一种可能的结果。
例如，假设某个模型用于区分样本属于动物、蔬菜还是矿物，一对多解决方案将提供下列三个单独的二元分类器：

• • 动物和非动物
  • 蔬菜和非蔬菜
  • 矿物和非矿物

候选采样 (candidate sampling)
一种训练时进行的优化，会使用某种函数（例如 softmax）针对所有正类别标签计算概率，但对于负类别标签，则仅针对其随机样本计算概率。
例如，如果某个样本的标签为“小猎犬”和“狗”，则候选采样将针对“小猎犬”和“狗”类别输出以及其他类别（猫、棒棒糖、栅栏）的随机子集计算预测概率和相应的损失项。
这种采样基于的想法是，只要正类别始终得到适当的正增强，负类别就可以从频率较低的负增强中进行学习，这确实是在实际中观察到的情况。
候选采样的目的是，通过不针对所有负类别计算预测结果来提高计算效率。

逻辑回归 (logistic regression)
一种模型，通过将 S 型函数应用于线性预测，生成分类问题中每个可能的离散标签值的概率。
虽然逻辑回归经常用于二元分类问题，但也可用于多类别分类问题（其叫法变为多类别逻辑回归或多项回归）。

softmax
一种函数，可提供多类别分类模型中每个可能类别的概率。这些概率的总和正好为 1.0。
例如，softmax 可能会得出某个图像是狗、猫和马的概率分别是 0.9、0.08 和 0.02。（也称为完整 softmax。）
与候选采样相对。