机器学习入门08 - 表示法 (Representation)

原文链接：https://developers.google.com/machine-learning/crash-course/representation/

机器学习模型不能直接看到、听到或感知输入样本。
必须创建数据表示，为模型提供有用的信号来了解数据的关键特性。
也就是说，为了训练模型，必须选择最能代表数据的特征集。

1- 特征工程

机器学习的关注点是特征表示，也就是说，开发者通过添加和改善特征来调整模型。

1.1- 将原始数据映射到特征

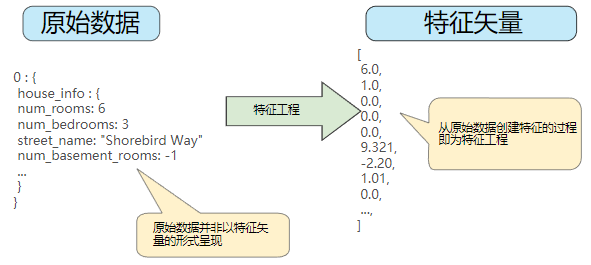
左侧表示来自输入数据源的原始数据，右侧表示特征矢量，也就是组成数据集中样本的浮点值集。

特征工程指的是将原始数据转换为特征矢量，也就是说，是将原始数据映射到机器学习特征。
进行特征工程预计需要大量时间。
许多机器学习模型都必须将特征表示为实数向量，因为特征值必须与模型权重相乘。

1.2- 映射数值

整数和浮点数据不需要特殊编码，因为它们可以与数字权重相乘。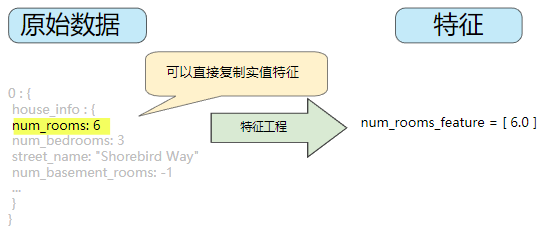

1.3- 映射分类值

分类特征具有一组离散的可能值。
由于模型不能将字符串与学习到的权重相乘，因此使用特征工程将字符串转换为数字值。
实现方法：

1. 定义一个从特征值（可能值的词汇表）到整数的映射。
2. 将所有其他可能值词汇分组为一个全部包罗的“其他”类别，称为 OOV（词汇表外）分桶。

但如果将这些索引数字直接纳入到模型中，将会造成一些可能存在问题的限制：

• 模型没有灵活地学习不同的权重，而是学习了适用于所有可能值的单一权重
• 特征值可能有多个值

如何去除以上限制？
可以为模型中的每个分类特征创建一个二元向量来表示这些值

• 对于适用于样本的值，将相应向量元素设为 1。
• 将所有其他元素设为 0。

该向量的长度等于词汇表中的元素数。
当只有一个值为 1 时，这种表示法称为独热编码；当有多个值为 1 时，这种表示法称为多热编码。
该方法能够有效地为每个特征值创建布尔变量。

1.4- 稀疏表示法 (sparse representation)

一种张量表示法，仅存储非零元素。
可以避免占用大量的存储空间并耗费很长的计算时间。
在稀疏表示法中，仍然为每个特征值学习独立的模型权重。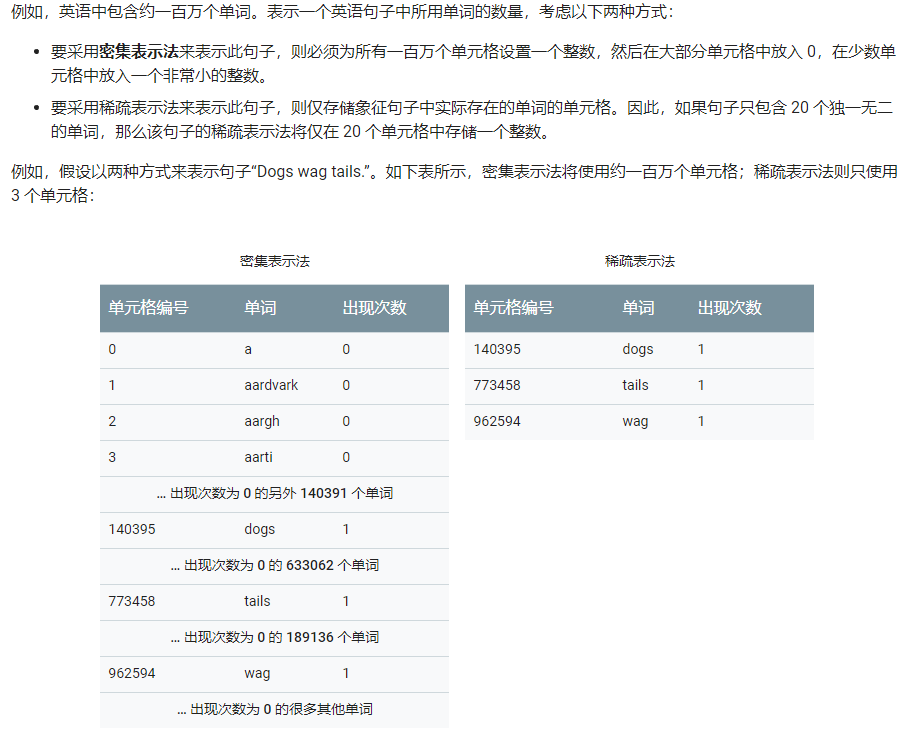

2- 良好特征的特点 

什么样的值才算特征矢量中良好的特征？

2.1- 避免很少使用的离散特征值

良好的特征值应该在数据集中出现大约 5 次以上，模型就可以学习该特征值与标签是如何关联的。
也就是说，大量离散值相同的样本可让模型有机会了解不同设置中的特征，从而判断何时可以对标签很好地做出预测。
相反，如果某个特征的值仅出现一次或者很少出现，则模型就无法根据该特征进行预测。

2.2- 最好具有清晰明确的含义

每个特征对于项目中的任何人来说都应该具有清晰明确的含义。
在某些情况下，混乱的数据（而不是糟糕的工程选择）会导致含义不清晰的值。

2.3- 不要将“神奇”的值与实际数据混为一谈

良好的浮点特征不包含超出范围的异常断点或“神奇”的值。
如果某个特征的值包含“神奇值”，为解决这个问题，需将该特征转换为两个特征：

• 一个特征只存储特征的值，但不含神奇值
• 一个特征存储布尔值，表示是否提供了该特征

2.4- 考虑上游不稳定性

特征的定义不应随时间发生变化。
例如，城市名称一般不会改变，但城市的电话号码前缀这种表示在未来运行其他模型时可能轻易发生变化。

3- 清理数据

在实际应用机器学习过程中，将花费大量的时间挑出坏样本并加工可以挽救的样本。
即使是非常少量的坏样本也会破坏掉一个大规模数据集。

3.1- 缩放特征值

缩放是指将浮点特征值从自然范围（例如 100 到 900）转换为标准范围（例如 0 到 1 或 -1 到 +1）。
如果某个特征集只包含一个特征，则缩放可以提供的实际好处微乎其微或根本没有。
不过，如果特征集包含多个特征，则缩放特征可以带来以下优势：

• 帮助梯度下降法更快速地收敛。
• 帮助避免“NaN 陷阱”。在这种陷阱中，模型中的一个数值变成 NaN（例如，当某个值在训练期间超出浮点精确率限制时），并且模型中的所有其他数值最终也会因数学运算而变成 NaN。
• 帮助模型为每个特征确定合适的权重。如果没有进行特征缩放，则模型会对范围较大的特征投入过多精力。

不需要对每个浮点特征进行完全相同的缩放。
即使特征 A 的范围是 -1 到 +1，同时特征 B 的范围是 -3 到 +3，也不会产生什么恶劣的影响。
不过，如果特征 B 的范围是 5000 到 100000，模型会出现糟糕的响应。

3.2- 处理极端离群值

如何最大限度降低这些极端离群值的影响？
一种方法是对每个值取对数，另一种方法是限制限制特征值的范围
注意：

将特征值限制到某个数值并不意味着会忽略所有大于此数值的特征值。
而是说，所有大于指定数值的特征值都将变成这个指定数值。
尽管这样处理，在曲线图中可能会存在“这个指定数值之后出现小峰值”的现象，但是缩放后的特征集现在依然比原始数据有用。

3.3- 分箱(binning)

将一个特征（通常是连续特征）转换成多个二元特征（称为桶或箱），通常根据值区间进行转换。
如果按分位数分箱可以确保每个桶内的样本数量是相等的，完全无需担心离群值。
例如，可以将温度区间分割为离散分箱，而不是将温度表示成单个连续的浮点特征。
假设温度数据可精确到小数点后一位，则可以将介于 0.0 到 15.0 度之间的所有温度都归入一个分箱，将介于 15.1 到 30.0 度之间的所有温度归入第二个分箱，并将介于 30.1 到 50.0 度之间的所有温度归入第三个分箱。

3.4- 清查

在现实生活中，数据集中的很多样本是不可靠的，原因有以下一种或多种：

• 遗漏值。 例如，有人忘记为某个房屋的年龄输入值。
• 重复样本。 例如，服务器错误地将同一条记录上传了两次。
• 不良标签。 例如，有人错误地将一颗橡树的图片标记为枫树。
• 不良特征值。 例如，有人输入了多余的位数，或者温度计被遗落在太阳底下。

一旦检测到存在这些问题，通常需要将相应样本从数据集中移除，从而“修正”不良样本。
要检测遗漏值或重复样本，可以编写一个简单的程序。
检测不良特征值或标签可能会比较棘手。

除了检测各个不良样本之外，还必须检测集合中的不良数据。
直方图是一种用于可视化集合中数据的很好机制。
此外，收集如下统计信息也会有所帮助：

• 最大值和最小值
• 均值和中间值
• 标准偏差

考虑生成离散特征的最常见值列表，便于直观检查。

3.5- 了解数据

遵循以下规则：

• 记住您预期的数据状态。
• 确认数据是否满足这些预期（或者解释为何数据不满足预期）。
• 仔细检查训练数据是否与其他来源（例如信息中心）的数据一致。

像处理任何任务关键型代码一样谨慎处理数据。良好的机器学习依赖于良好的数据。

4- 练习

xxx

5- 关键词

表示法 (representation)
将数据映射到实用特征的过程。

分类特征(分类数据，categorical data)
一种特征，拥有一组离散的可能值。
以某个名为 house style 的分类特征为例，该特征拥有一组离散的可能值（共三个），即 Tudor, ranch, colonial。
通过将 house style 表示成分类数据，相应模型可以学习 Tudor、ranch 和 colonial 分别对房价的影响。

有时，离散集中的值是互斥的，只能将其中一个值应用于指定样本。
例如，car maker 分类特征可能只允许一个样本有一个值 (Toyota)。
在其他情况下，则可以应用多个值。
一辆车可能会被喷涂多种不同的颜色，因此，car color 分类特征可能会允许单个样本具有多个值（例如 red 和 white）。

分类特征有时称为离散特征。
与数值数据相对。

离散特征 (discrete feature)
一种特征，包含有限个可能值。
例如，某个值只能是“动物”、“蔬菜”或“矿物”的特征便是一个离散特征（或分类特征）。
与连续特征相对。

特征工程 (feature engineering)
指以下过程：确定哪些特征可能在训练模型方面非常有用，然后将日志文件及其他来源的原始数据转换为所需的特征。
在 TensorFlow 中，特征工程通常是指将原始日志文件条目转换为 tf.Example 协议缓冲区。
特征工程有时称为特征提取。

独热编码 (one-hot encoding)
一种稀疏向量，其中：
一个元素设为 1。
所有其他元素均设为 0。
独热编码常用于表示拥有有限个可能值的字符串或标识符。
例如，假设某个指定的植物学数据集记录了 15000 个不同的物种，其中每个物种都用独一无二的字符串标识符来表示。
在特征工程过程中，您可能需要将这些字符串标识符编码为独热向量，向量的大小为 15000。

缩放 (scaling)
特征工程中的一种常用做法，是指对某个特征的值区间进行调整，使之与数据集中其他特征的值区间一致。
例如，假设您希望数据集中所有浮点特征的值都位于 0 到 1 区间内，如果某个特征的值位于 0 到 500 区间内，您就可以通过将每个值除以 500 来缩放该特征。
另请参阅标准化。

标准化 (normalization)
将实际的值区间转换为标准的值区间（通常为 -1 到 +1 或 0 到 1）的过程。
例如，假设某个特征的自然区间是 800 到 6000。通过减法和除法运算，您可以将这些值标准化为位于 -1 到 +1 区间内。
另请参阅缩放。

特征集 (feature set)
训练机器学习模型时采用的一组特征。
例如，对于某个用于预测房价的模型，邮政编码、房屋面积以及房屋状况可以组成一个简单的特征集。

NaN 陷阱 (NaN trap)
模型中的一个数字在训练期间变成 NaN，这会导致模型中的很多或所有其他数字最终也会变成 NaN。
NaN 是“非数字”的缩写。

离群值 (outlier)
与大多数其他值差别很大的值。在机器学习中，下列所有值都是离群值。
绝对值很高的权重。
与实际值相差很大的预测值。
值比平均值高大约 3 个标准偏差的输入数据。
离群值常常会导致模型训练出现问题。