机器学习入门02 - 深入了解 (Descending into ML)
原文链接:https://developers.google.com/machine-learning/crash-course/descending-into-ml/
线性回归是一种找到最适合一组点的直线或超平面的方法。
1- 线性回归
线性回归是一种找到最适合一组点的直线或超平面的方法。
以数学形式表达:$y = mx + b$
- y指的是试图预测的值
- m指的是直线的斜率
- x指的是输入特征的值
- b指的是 y 轴截距
按照机器学习的惯例来书写此方程式:
$y' = b + w_1x_1$
2- 训练与损失
简单来说,训练模型表示通过有标签样本来学习(确定)所有权重和偏差的理想值。
在监督式学习中,机器学习算法构建模型的方式:检查多个样本并尝试找出可最大限度地减少损失的模型;这一过程称为经验风险最小化。
损失是一个数值,表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确,则损失为零,否则损失会较大。
训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。
能否创建一个数学函数(损失函数),以有意义的方式汇总各个损失?
平方损失(L2 损失)
平方损失是一种常见的损失函数。
单个样本的平方损失是“标签值与预测值两者差平方”:(observation - prediction(x))2 ,也就是 (y - y')2
均方误差 (MSE) 指的是每个样本的平均平方损失。
要计算 MSE,请求出各个样本的所有平方损失之和,然后除以样本数量。
$MSE = \frac{1}{N} \sum_{(x,y)\in D} (y - prediction(x))^2$
- (x, y)指的是样本,其中x指的是模型进行预测时使用的特征集,y指的是样本的标签。
- prediction(x)指的是权重和偏差与特征集x结合的函数。
- D指的是包含多个有标签样本(即(x, y))的数据集。
- N指的是D中的样本数量。
虽然 MSE 常用于机器学习,但它既不是唯一实用的损失函数,也不是适用于所有情形的最佳损失函数。
3- 理解
问题
对于以下曲线图中显示的两个数据集,哪个数据集的均方误差 (MSE) 较高?
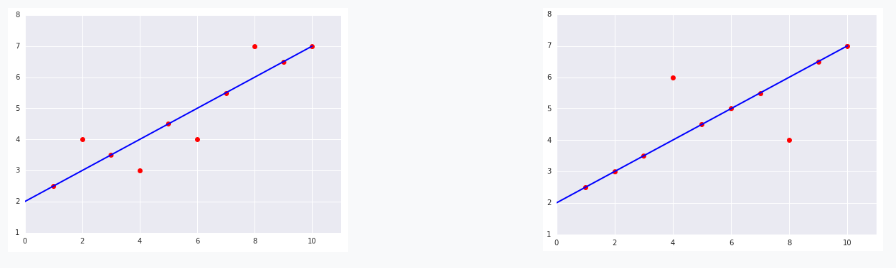
解答
右侧的数据集。--- 正确
线上的 8 个样本产生的总损失为 0。不
过,尽管只有两个点在线外,但这两个点的离线距离依然是左图中离群点的 2 倍。
平方损失进一步加大差异,因此两个点的偏移量产生的损失是一个点的 4 倍。
$MSE = \frac{0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2} {10} = 0.8$
左侧的数据集。
线上的 6 个样本产生的总损失为 0。
不在线上的 4 个样本离线并不远,因此即使对偏移求平方值,产生的值仍然很小:
$MSE = \frac{0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 0^2} {10} = 0.4$
4- 关键词
偏差 (bias)
距离原点的截距或偏移。偏差(也称为偏差项)在机器学习模型中用 b 或 w0 表示。
例如,在下面的公式中,偏差为 b:
$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$
请勿与预测偏差混淆。
权重 (weight)
线性模型中特征的系数,或深度网络中的边。
训练线性模型的目标是确定每个特征的理想权重。
如果权重为 0,则相应的特征对模型来说没有任何贡献。
线性回归 (linear regression)
一种回归模型,通过将输入特征进行线性组合输出连续值。
推断 (inference)
在机器学习中,推断通常指以下过程:通过将训练过的模型应用于无标签样本来做出预测。
在统计学中,推断是指在某些观测数据条件下拟合分布参数的过程。(请参阅维基百科中有关统计学推断的文章。)
经验风险最小化 (ERM, empirical risk minimization)
用于选择可以将基于训练集的损失降至最低的函数。与结构风险最小化相对。
损失 (Loss)
一种衡量指标,用于衡量模型的预测偏离其标签的程度。或者更悲观地说是衡量模型有多差。
要确定此值,模型必须定义损失函数。
例如,线性回归模型通常将均方误差用作损失函数,而逻辑回归模型则使用对数损失函数。
均方误差 (MSE, Mean Squared Error)
每个样本的平均平方损失。MSE 的计算方法是平方损失除以样本数。
TensorFlow Playground 显示的“训练损失”值和“测试损失”值都是 MSE。
平方损失函数 (squared loss)
在线性回归中使用的损失函数(也称为 L2 损失函数)。
该函数可计算模型为有标签样本预测的值和标签的实际值之差的平方。
由于取平方值,因此该损失函数会放大不佳预测的影响。
也就是说,与 L1 损失函数相比,平方损失函数对离群值的反应更强烈。
训练 (training)
确定构成模型的理想参数的过程。
行动是绝望的解药!
欢迎转载和引用,但请在明显处保留原文链接和原作者信息!
本博客内容多为个人工作与学习的记录,少数内容来自于网络并略有修改,已尽力标明原文链接和转载说明。如有冒犯,即刻删除!
以所舍,求所得,有所获,方所成。



