【学习总结】《大话数据结构》- 第6章-树

【学习总结】《大话数据结构》- 总

第6章树-代码链接

启示：

  • 树

目录

========================================

6.1 开场白

  • 一些可以略过的场面话...

========================================

6.2 树的定义

  • 定义


  • 注意：

    • n>0时：根节点是唯一的，不可能存在多个根节点。

    • m>0时：子树的个数没有限制，但它们一定互不相交。

  • 结点分类

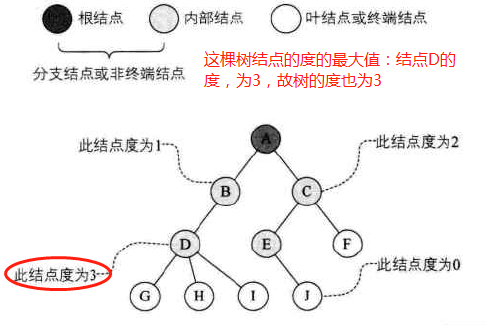
    • 结点的度（degree）：结点拥有的子树数

    • 叶结点（leaf）或终结点：度为0的结点

    • 非终端结点或分支结点：度不为0的结点

    • 内部结点：除根节点外，分支结点也称为内部结点

    • 树的度：树内各结点的度的最大值

  • 结点间关系

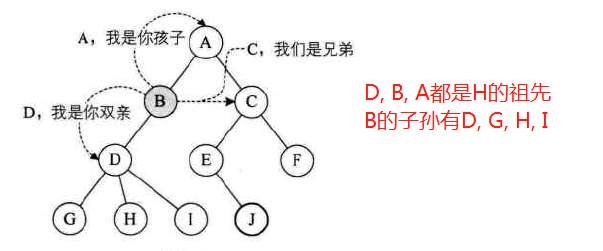
    • 孩子（child）：结点的子树的根称为该结点的孩子

    • 双亲（parent）：该结点称为孩子的双亲（父母同体，唯一的一个）

    • 兄弟（sibling）：同一个双亲的孩子之间互称兄弟

    • 祖先：结点的祖先是从根到该结点所经分支上的所有结点

    • 子孙：以某结点为根的子树中的任一结点都称为该节点的子孙

  • 树的其他相关概念

    • 层次（level）：从根开始定义起，根为第一层，根的孩子为第二层

      即：若某结点在第L层，则其子树的根就在第L+1层

    • 堂兄弟：双亲在同一层的结点互为堂兄弟

    • 深度（depth）或高度：树中结点的最大层次称为树的深度或高度

  • 有序树/无序树：如果将树中结点的各子树看成从左至右有次序的，不能互换的，则称该树为有序树，否则为无序树。

  • 森林（forest）：m（m>=0）棵互不相交的树的集合。

    • 对于树中每个结点而言，其子树的集合即为森林。

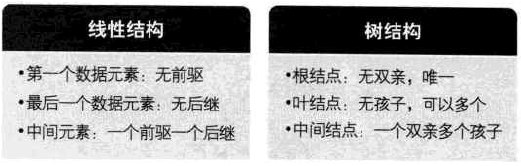
  • 线性表与树的对比

========================================

6.3 树的抽象数据类型

  • 相比线性结构，树的操作就完全不同了。以下是基本和常用操作。

========================================

6.4 树的存储结构

  • 简单的顺序存储结构无法直接反映逻辑关系，不能满足树的实现要求

    故充分利用顺序存储和链式存储结构的特点，介绍三种不同的表示法

  • 双亲表示法

    • 引入：除根节点外，其余每个结点，不一定有孩子，但一定有且仅有一个双亲

    • 定义：设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。

      • data：数据域，存储结点的数据信息

      • parent：指针域，存储该结点的双亲在数组中的下标

      • 约定：根节点的位置域为-1

  • 代码实现：


  • 图示：

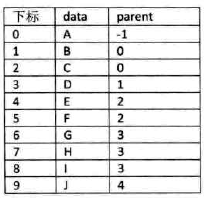
  • 弊端：找一个结点的双亲，时间复杂度O(1)，但是找一个结点的孩子，需要遍历整个结构

  • 针对上述找孩子的解决：增设一个结点最左边孩子的域（长子域），没有孩子的结点，长子域为-1

    • 2个孩子：知道长子是谁，另一个就是次子了

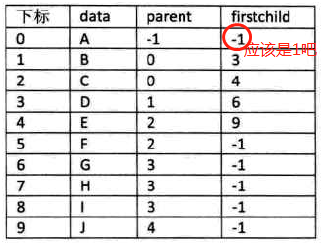
  • 另一个问题：兄弟之间的关系 -- 增加一个右兄弟域来体现兄弟关系，没有右兄弟时为-1

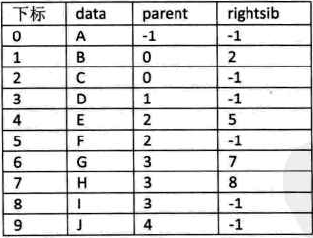
  • 同时关注结点的双亲、孩子、兄弟时：设置双亲域、长子域、右兄弟域

    但对时间遍历要求较高，有需要时再添加相应的结构

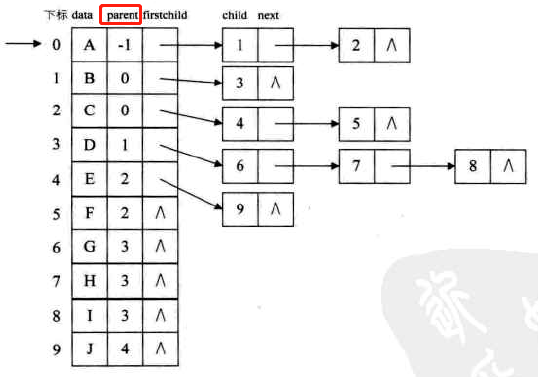
  • 孩子表示法

    • 多重链表表示法：

      • 每个结点有多个指针域，其中每个指针指向一棵子树的根节点，这种方法叫做多重链表表示法。

    • 方案一：设置指针域的个数为树的度

      • 可能存在空间的浪费




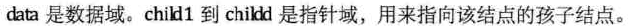
  • 方案二：设置每个结点指针域的个数等于该结点的度，取一个位置来存储结点指针域的个数

    • 空间利用率提高，但是各个结点的链表结构不同，要维护结点的度的数值，时间损耗提高




  • 孩子表示法：

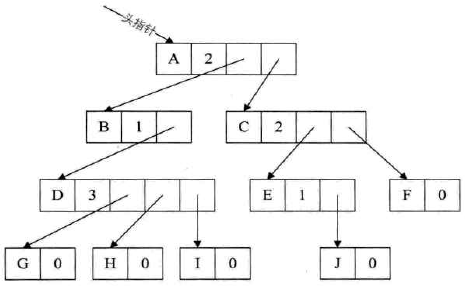
    • 把每个结点的孩子结点排列起来，以单链表作存储结构，则n个结点有n个孩子链表，如果是叶子结点，则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中。


  • 孩子表示法的两种结点结构

    • 孩子链表的孩子结点



- ### 表头数组的表头结点

  • 孩子表示法的结构定义代码：


  • 孩子表示法的弊端：找某结点的双亲，仍需要遍历整个树

  • 改进：双亲孩子表示法

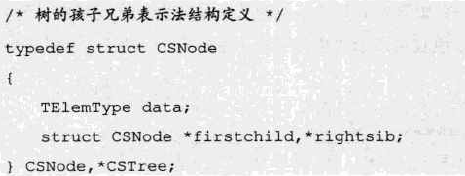
  • 孩子兄弟表示法

    • 引入：

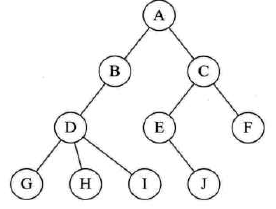
      任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。

      因此，可以设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟


  • 结构定义代码：

  • 图示：


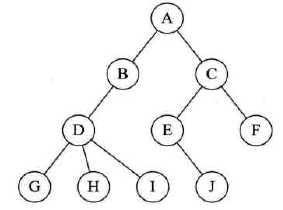
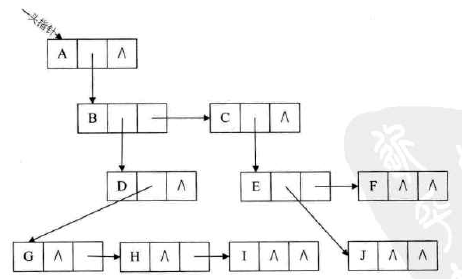
  • 弊端：找双亲仍需遍历整棵树，可以增加parent指针域

  • 好处：把一棵复杂的树变成了一棵二叉树

========================================

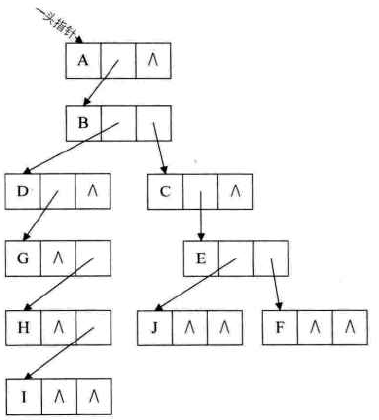
6.5 二叉树的定义

  • 定义


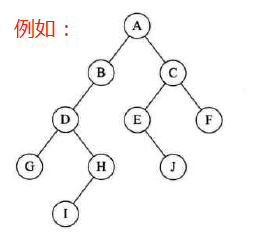
  • 1、二叉树的特点




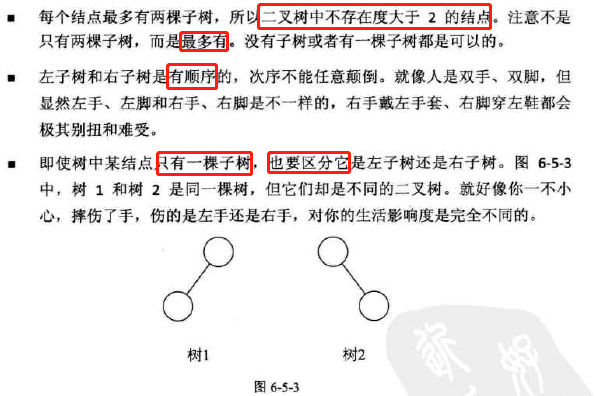
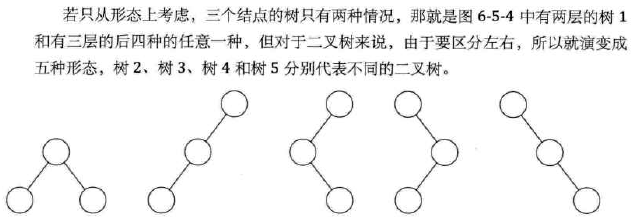
  • 2、特殊二叉树

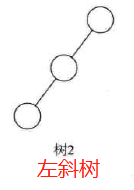
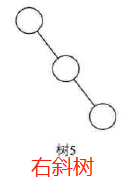
    • 1-斜树：

      所有结点都只有左子树的二叉树叫左斜树

      所有结点都只有右子树的二叉树叫右斜树

      这两者统称为斜树。

      特点：每层只有一个结点，结点个数与二叉树的深度相同

      注：线性表结构可以理解为是树的一种极其特殊的表现形式

  • 2、满二叉树

    定义：一棵二叉树中，所有分支结点都存在左右子树，并且所有叶子都在同一层


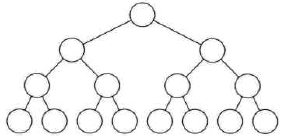
#### 特点：

  • 3、完全二叉树

    • 定义：对一棵具有n个结点的二叉树按层序编号，如果编号i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则此二叉树为完全二叉树

      完全二叉树示例：


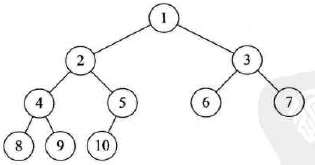
#### 非完全二叉树示例：

- #### 完全二叉树的特点：

- #### 完全二叉树的判断方法：给每个结点按满二叉树的结构逐层排序，如果编号出现空档，就不是，否则就是。

========================================

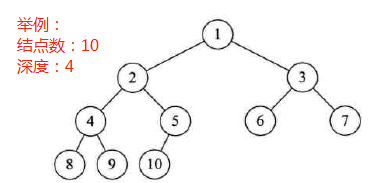
6.6 二叉树的性质




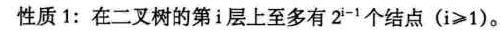
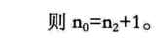
  • 推导：




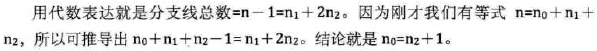
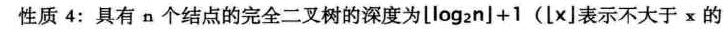
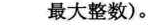
  • 简单推导：




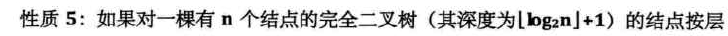
  • 举例：


========================================

6.7 二叉树的存储结构

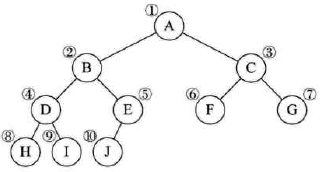
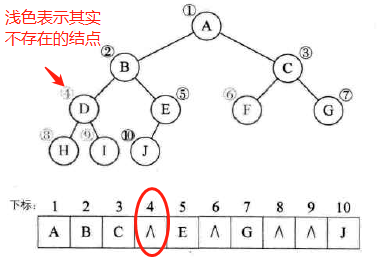
  • 二叉树的顺序存储结构：按完全二叉树编号

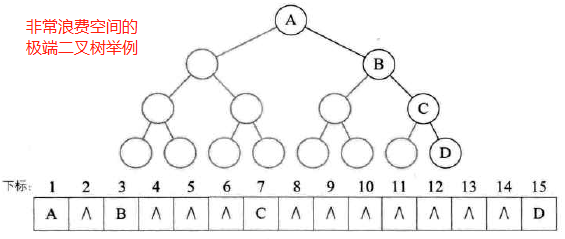
    • 顺序存储结构一般只用于完全二叉树，否则容易造成空间的浪费

    • 完全二叉树：


  • 一般二叉树：

  • 极端情况的二叉树：

  • 二叉链表

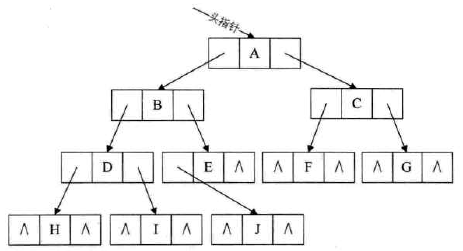
    • 定义：

      二叉树每个结点最多有两个孩子，所以设置一个数据域和两个指针域，这样的链表称为二叉链表。


- data：数据域
- lchild和lchild：指针域，分别存放指向左孩子和右孩子的指针。

  • 二叉链表的结点结构定义代码

  • 图示：

  • 三叉链表：

    • 如有需要，可增加一个指向其双亲的指针域，其称为三叉链表。

========================================

6.8 遍历二叉树

  • 二叉树遍历原理

  • 关键词：访问和次序

  • 访问：根据实际的需求来确定具体做什么，算作是一个抽象操作。

  • 遍历次序：

    • 线性结构最多是从头到尾、循环、双向等。

    • 树节点不存在唯一前驱后继，会因为遍历方式不同而产生完全不同的结果。

  • 二叉树遍历方法：

    • 四种：前序遍历、中序遍历、后序遍历、层序遍历。

    • 前序遍历：根左右


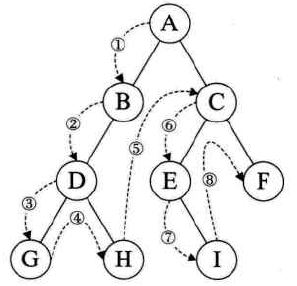
  • 中序遍历：左根右


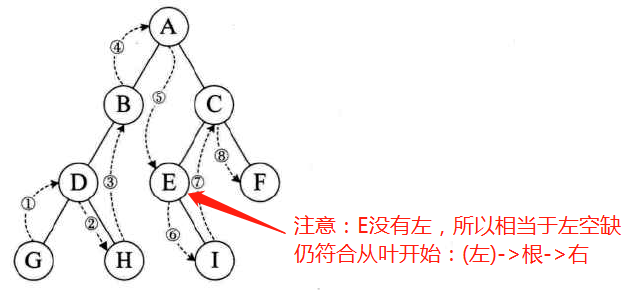
  • 后序遍历：左右根


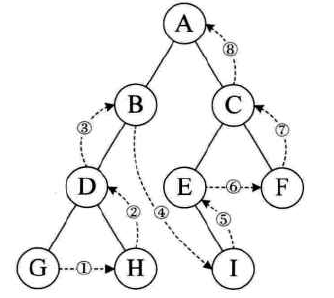
  • 层序遍历：


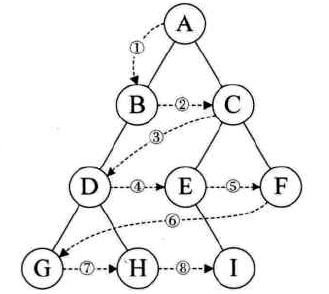
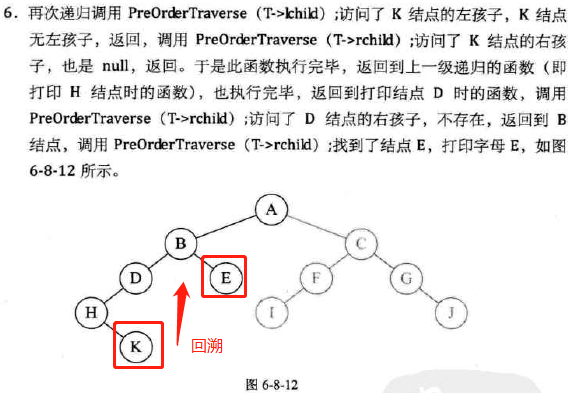
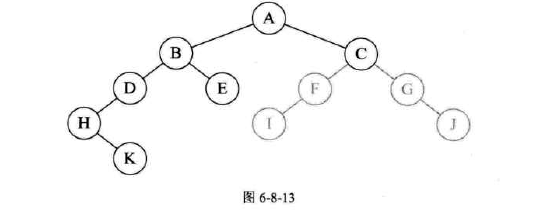
  • 前序遍历

    • 代码实现;

  • 图示：










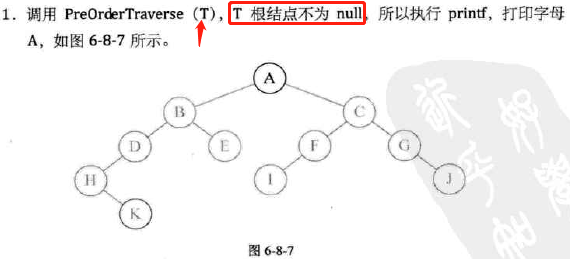
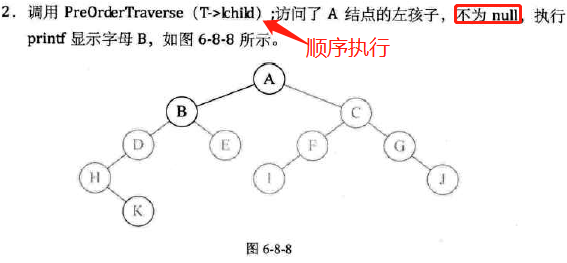
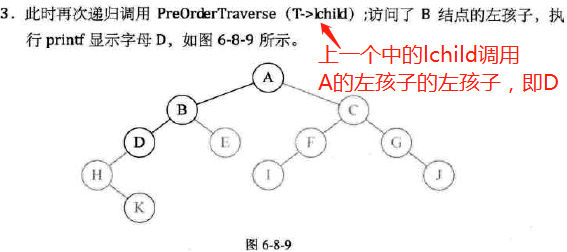
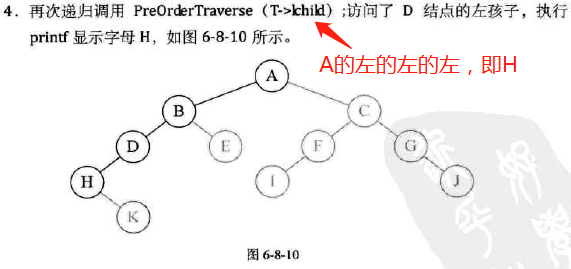
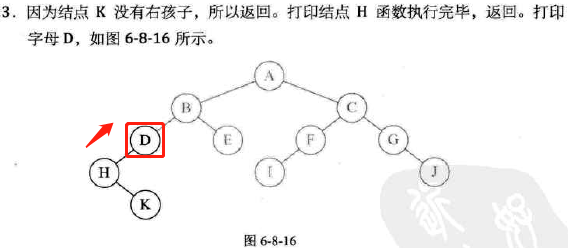
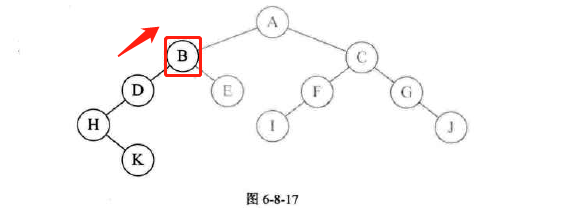
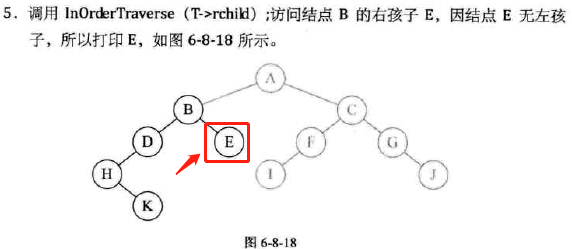
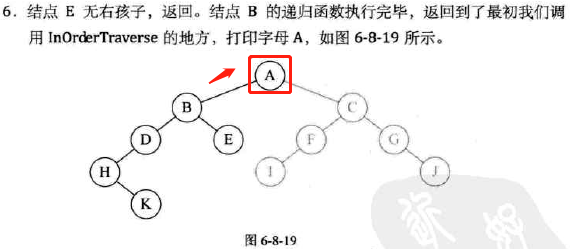
  • 中序遍历

    • 代码实现

  • 图示：









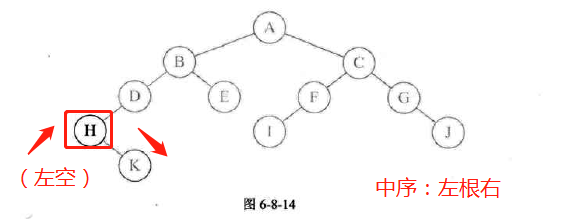
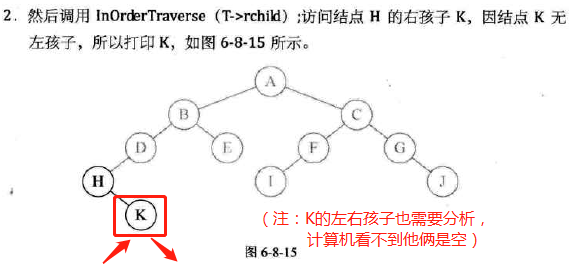
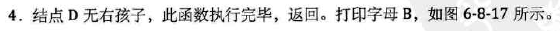
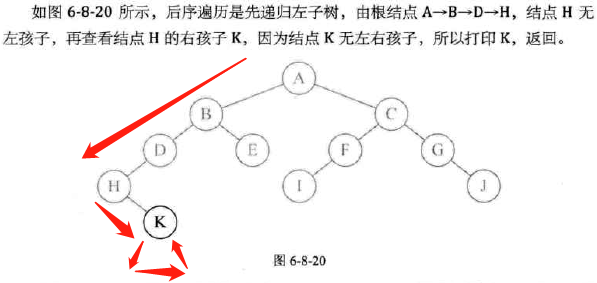
  • 后序遍历

    • 代码实现：

  • 图示：


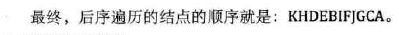
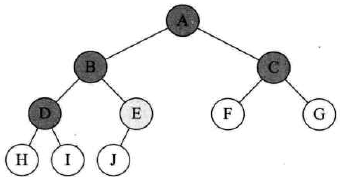
  • 遍历推导

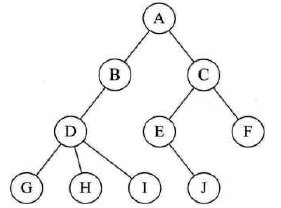
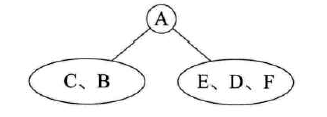
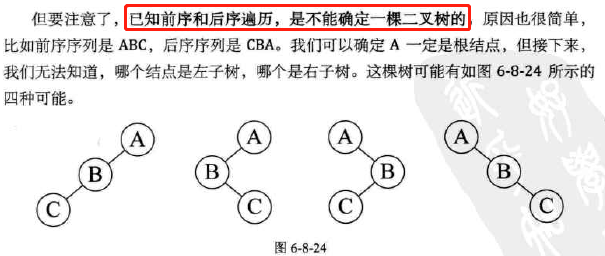
    • 已知前序遍历和中序遍历，求后序遍历

      前序：ABCDEF，中序：CBAEDF

      • 前序第一个字母是A，说明A是根节点
      • 中序CBAEDF，说明CB在A的左，EDF在A的右
      • 前序CB：ABCDEF，先B后C，故B是A的左，C是B的孩子，左右不确定
      • 中序CB：CBAEDF，先C后B，故C是B的左
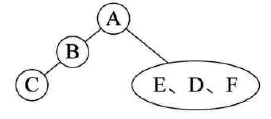
      • 前序EDF：ABCDEF，说明D是A的右孩子，EF是D的子孙
      • 中序EDF：CBAEDF，E在D左，F在D右，说明E是D的左孩子，F是D的右孩子
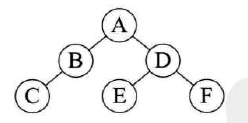
      • 根据得到的二叉树图，检查一下是否符合所给前序和中序
      • 然后可得后序：CBEFDA

    • 已知中序遍历和后序遍历，求前序遍历：

  • 性质小结：


========================================

6.9 二叉树的建立

  • 二叉树的扩展二叉树：

    • 为了能让每个结点确认是否有左右孩子，将每个结点的空指针引出一个虚结点，其值为一特定值，比如"#"

    • 称这种处理后的二叉树为原二叉树的扩展二叉树

    • 扩展二叉树就可以做到一个遍历序列确定一棵二叉树

  • 代码实现：


  • 其他：

    • 当然，也可以用中序或后序遍历的方式实现二叉树的建立

      只需对代码里生成结点和构造左右子树的代码顺序交换，并且输入字符也做相应的更新即可。

========================================

6.10 线索二叉树

  • 引入：

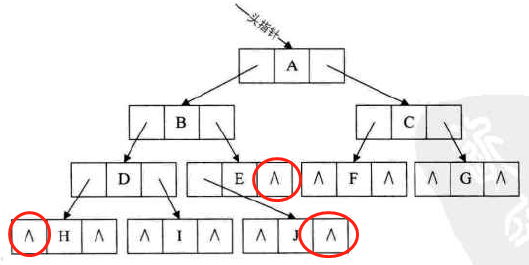
    • 空指针存在空间的浪费

  • 二叉链表中，只能看出左右孩子，而看不出某序遍历的前驱和后继

  • 定义：

    • 线索：指向前驱和后继的指针称为线索

    • 线索链表：加上线索的二叉链表称为线索链表

    • 线索二叉树（Threaded Binary Tree）：相应的二叉树称为线索二叉树


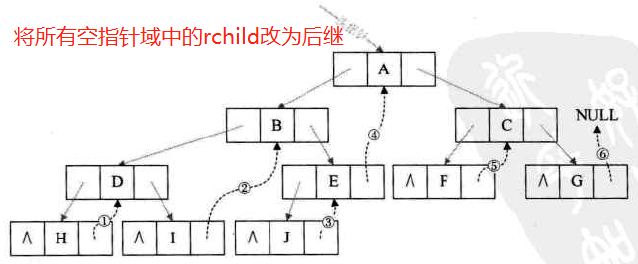
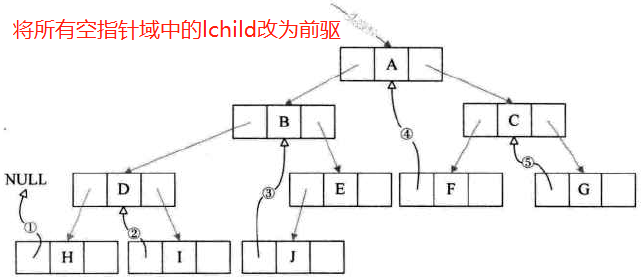
  • 线索化：对二叉树以某种次序遍历使其变为线索二叉树的过程


（此处应该是把非空指针域也变成了线索）

  • 为区分左右孩子和前驱后继，每个结点增设两个标志域

（注：此标志域占用的内存空间小于rchild类的指针变量）


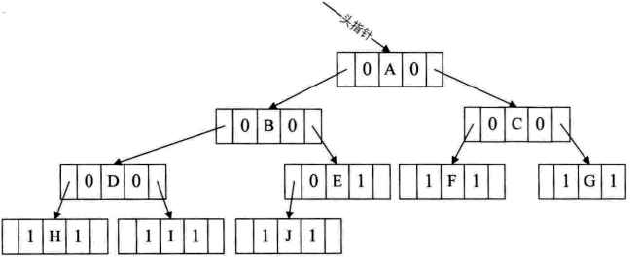
  • 线索二叉树的结构实现

  • 前驱和后继的信息只有在遍历二叉树时才能得到

  • 所以线索化的过程就是在遍历的过程中修改空指针的过程。

  • 代码实现：中序遍历线索化



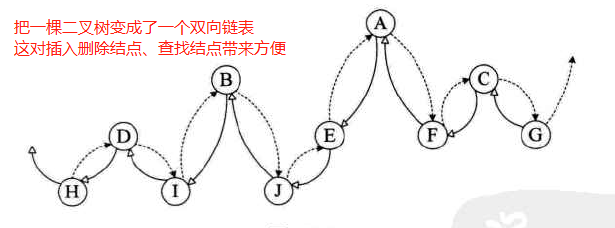
  • 类双向链表图示：

  • 类双向链表代码实现：




========================================

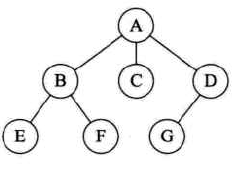
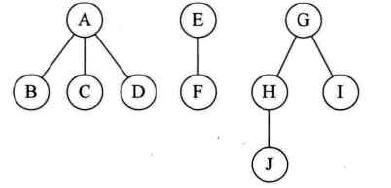
6.11 树、森林与二叉树的转换

  • 树转换为二叉树


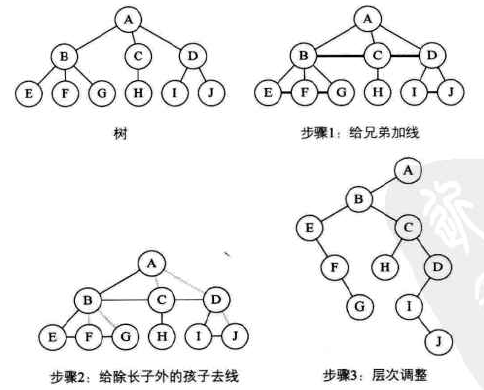
  • 森林转换为二叉树


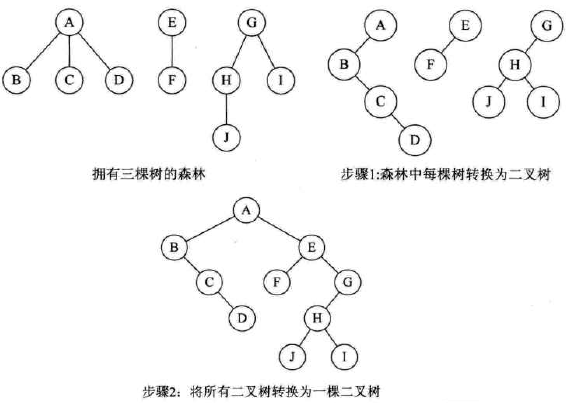
  • 二叉树转换为树



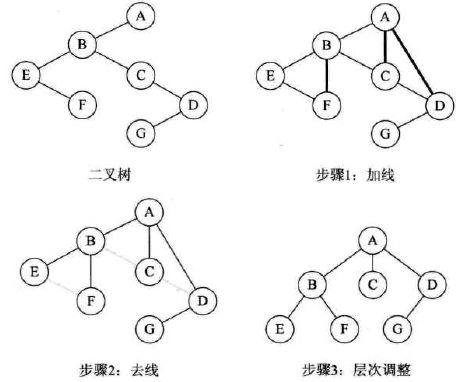
  • 二叉树转换为森林

    • 首先判断：二叉树的根结点是否有右孩子：有就是森林，否则不是。


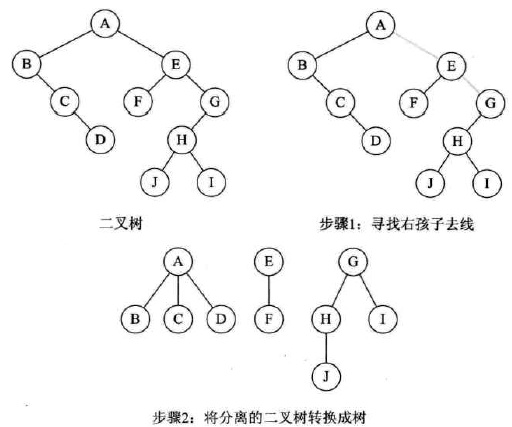
  • 树和森林的遍历






========================================

6.12 赫夫曼树及其应用

  • 定义

  • 路径：从树中一个结点到另一个结点之间的分支构成两个结点之间的路径

  • 路径长度：路径上的分支数目称为路径长度

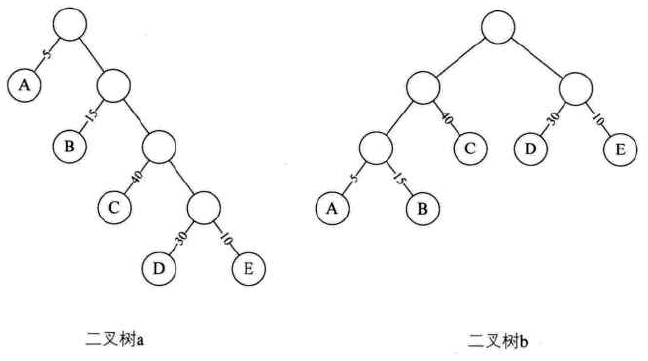
  • 树的路径长度：从树根到每个结点的路径长度（注意是每一结点，不止是所有叶结点）

    树a的路径长度：

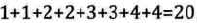
    树b的路径长度：

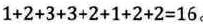
  • 结点的带权路径长度：从该结点到树根之间的路径长度与结点上权值的乘积。

  • 树的带权路径长度：树中所有叶子结点的带权路径长度。（注意是叶子结点，没有中间的）

  • 赫夫曼树（Huffman）：带权路径长度WPL最小的二叉树称做赫夫曼树。也叫最优二叉树。

    • 注：哈夫曼树中没有度为1的结点。（每一个结点都是由它的两棵子树合并产生的新结点）


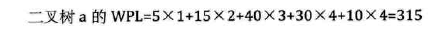
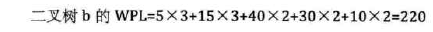
  • 构造最优的赫夫曼树


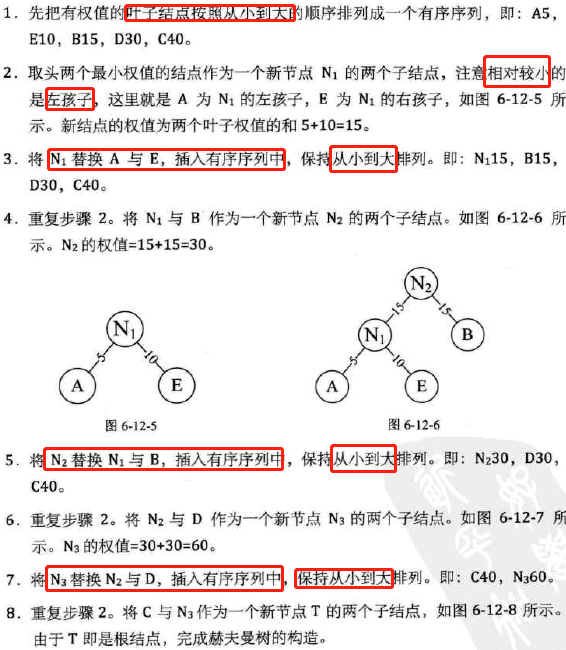
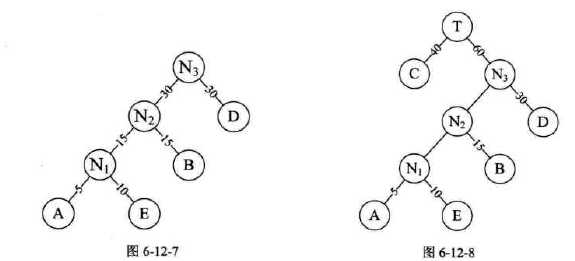
  • 构造赫夫曼树的赫夫曼算法描述：

  • 赫夫曼编码




========================================

6.13 总结回顾

========================================

6.14 结尾语

END

posted @ 2019-07-29 09:11  anliux  阅读(1132)  评论(0)  编辑  收藏  举报