【学习总结】《大话数据结构》- 第3章-线性表

【学习总结】《大话数据结构》- 总

第3章线性表-代码链接

启示：

• 线性表：零个或多个数据元素的有限序列。

目录

• 3.1 开场白
• 3.2 线性表的定义
• 3.3 线性表的抽象数据类型
• 3.4 线性表的顺序存储结构
• 3.5 顺序存储结构的插入与删除
• 3.6 线性表的链式存储结构
• 3.7 单链表的读取
• 3.8 单链表的插入与删除
• 3.9 单链表的整表创建
• 3.10 单链表的整表删除
• 3.11 单链表结构与顺序存储结构优缺点
• 3.12 静态链表
• 3.13 循环链表
• 3.14 双向链表
• 3.15 总结回顾
• 3.16 结尾语

========================================

3.1 开场白

• 一些可以略过的场面话...
• 由一个例子引入：幼儿园小朋友排队，左右两侧每次都是固定的人，方便清点和避免丢失。

========================================

3.2 线性表的定义

• 定义：线性表（list）- 零个或多个数据元素的有限序列。

  • 几个关键点：

  1-“序列”：第一个元素无前驱，最后一个元素无后继，其他每个元素都有且只有一个前驱和后继。
  2-“有限”：元素的个数是有限的。
  3-再加一点：元素类型相同。

• 数学语言定义：

• 线性表的长度：线性表元素的个数n(n≥0)定义为线性表的长度。n=0时，称为空表。

  • 位序：ai是第i个数据元素，称i为数据元素ai在线性表中的位序。

• 一些线性表的例子：

  • 12星座-有序，有限，是线性表
  • 公司的组织架构，一个boss手下几个人那种：不是线性表，每个元素不只有一个后继。
  • 班级同学之间的友谊：不是线性关系，每个人都可以和多个同学建立友谊
  • 爱情：不是线性关系，否则每个人都有一个爱的人和被爱的人且不是同一个人....
  • 班级点名册：是线性表，按学号排序，有序有限，类型相同，并且作为复杂的线性表，一个数据元素由若干个数据项组成。
  • 书包占位所以要插队：不能，因为排队是线性表，而书包数据类型不同，别人都是人，书包不是人，所以不是线性表，不能插队。

========================================

3.3 线性表的抽象数据类型

• 第一章讲过“抽象数据类型”，大致包含类型名称、data、operation等

• 线性表的操作<对比幼儿园小朋友排队>：

  • 线性表的创建和初始化过程：老师给小朋友们排一个可以长期使用的队

  • 线性表重置为空表的操作：排好后发现高矮不一，于是解散重排

  • 根据位序得到数据元素：问到队伍里第5个小朋友是谁，老师很快能说出来这个小朋友的名字、家长等。

  • 查找某个元素：找一下麦兜是否是班里的小朋友，老师会告诉你，不是的

  • 插入数据和删除数据：有新来的小朋友，或者有小朋友生病请假时

• 线性表的抽象数据类型定义：

• 涉及更复杂的操作时，可以用以上的基本操作的组合来实现。

  • 例如求两个线性表集合A和B的并集：可以把存在B中但不存在A中的数据元素插入到A中

  

========================================

3.4 线性表的顺序存储结构

• 这部分了解一下线性表的两种物理结构之一----顺序存储结构

• 1-定义：线性表的顺序存储结构，指用一段地址连续的存储单元依次存储线性表的数据元素。

• 2-顺序存储方式：

  • 依次，每个数据元素类型相同，可以用c语言的一维数组来实现顺序存储结构。

  • 代码实现：

  

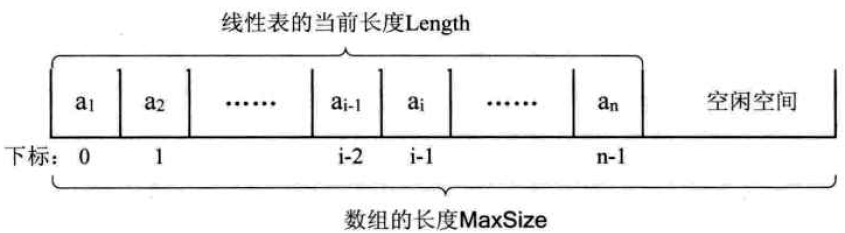
  • 描述顺序存储结构需要三个属性：

    • 1-存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置
    • 2-线性表的最大存储容量：数组长度MaxSize
    • 3-线性表的当前长度：length

• 3-数据长度和线性表长度的区别

  • 数组长度：是存放线性表的存储空间的长度，存储分配后这个量是一般不变的。

  • 线性表长度：线性表中数据元素的个数，随着插入删除操作而变化。

  • 注意：线性表的长度总是小于等于数组的长度。

• 4-地址的计算方法

  • 地址：存储器中的每个存储单元都有自己的编号，这个编号称为地址。（内存地址）

  • 计数：线性表从1开始，而c语言中的数组从0开始

  

  • LOC：获得存储位置的函数（假设每个数据元素占c个存储单元）

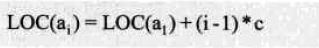
• 通过上述公式，可以随时算出线性表中任意位置的地址，且都是相同时间。

• 即时间复杂度：O(1) -- 每个位置存、取数据，都是相等的时间，也就是一个常数。

• 通常把具有这一特点的存储结构称为<随机存取结构>

========================================

3.5 顺序存储结构的插入与删除

• 0-注意点

  • 0.1-线性表的第 i 个数是从1开始计数，而数组下标[]是从0开始计数

  • 0.2-时刻保持清醒，分清到底是 i 还是 i-1

  • 0.3-L->data和L.data：（点出现在取数中，箭头出现在插入删除中）

    • L->data中L是结构体指针；L.data中L是结构体变量；一说：点适合顺序结构，箭头适合链式结构。

• 1-获得元素操作 - GetElem

• 2-插入操作

  • 图示：

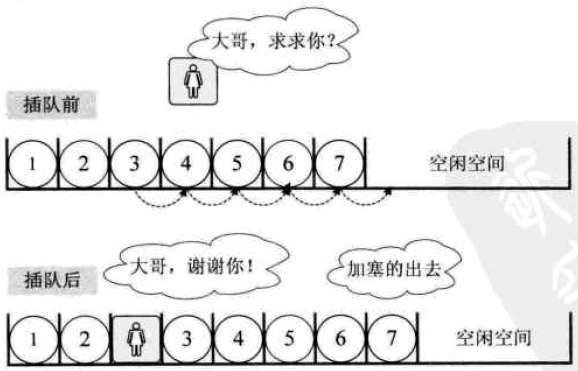
• 插入算法的思路：

  • 1-如果插入位置不合理，抛出异常；
  • 2-如果线性表长度大于等于数组长度，则抛出异常或动态增加容量；
  • 3-从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置；
    （注：从最后一个元素开始，依次往后挪一位，否则最后一个不动，前面没位置的）
  • 4-将要插入元素填入位置i处；
  • 5-表长加1.

• 代码实现：

（注：if中排除i>length+1是符合的，因为跟表不挨着，插入和表无关啦，而if中不包含临界点i=length+1的情况，因为if进行的是判断错误和移动数据，当i=length+1时，直接运行插入数据赋值即可，即if判断后的那条语句）

• 3-删除操作

  • 图示：

• 删除算法的思路：

  • 1-如果删除位置不合理，抛出异常；
  • 2-取出删除元素；
  • 3-从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置；
    （注：从删除元素的位置开始，依次往前挪，后面的跟上，就把空位补上了）
  • 4-表长减1.

• 代码实现：

• 4-插入、删除的时间复杂度分析：O(n)

  • 最好的情况：在最后一个位置插入或删除：O(1)

  • 最坏的情况：在第一个位置插入或删除：O(n)

  • 平均：(n-1)/2

• 5-线性表的顺序存储结构---不同操作的时间复杂度对比：

  • 存取操作：O(1)

  • 插入删除：O(n)

  • 综上：顺序存储结构适合元素个数不太变化的，更多是存取数据的应用

• 6-线性表的顺序存储结构的优缺点：

========================================

3.6 线性表的链式存储结构

• 1-顺序存储结构的不足的解决方法

  • 顺序存储的最大缺点：插入和删除需要移动大量元素，非常耗费时间。

  • 原因：相邻元素的存储位置也具有邻居关系，它们在内存中的位置是挨着的，无法快速介入。

  • 思路：不要考虑元素的相邻位置，只让每个元素知道它的下一个元素的地址，可以找到即可

• 2-线性表链式存储结构的定义

  • 特点：用一组任意的存储单元存储线性表的数据元素，这组存储单元可以连续，也可以不连续。（顺序存储要求地址连续）

  • 负担：顺序结构中，每个数据元素只需要存数据元素的信息，而链式结构中，还需要存储它的后继元素的存储地址。

  
  
  

  • 头指针：链表中第一个结点的存储位置叫做头指针。整个链表的存取从头指针开始。

  最后一个结点的指针：后继不存在，应为空，通常用NULL或“^”表示是

  

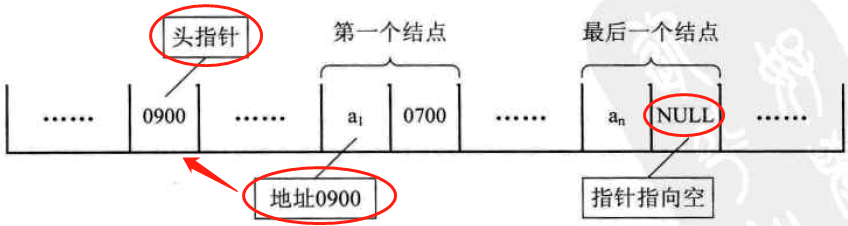
  • 头结点：为方便对链表进行操作，在单链表的第一个结点前附设一个结点，称为头结点。

  头结点的数据域可以不存储任何信息，也可以存储如线性表的长度等附加信息，头结点的指针域存储第一个结点的指针。

  

• 3-头结点与头指针的异同

• 注：头指针-->（头结点）-->开始结点（第一个结点）

  • 一个单链表可以由其头指针唯一确定，一般用其头指针来命名单链表
  • 不论链表是否为空，头指针总是非空
  • 单链表的头指针指向头结点。
  • 头结点的指针域存储指向第一结点的指针（即第一个元素结点的存储位置）
  • 若线性表为空表，则头结点的指针域为空。

• 参考：数据结构中的开始结点、头指针、头结点

• 4-线性表链式存储结构的代码描述

  • 空链表图示：线性表为空表，则头结点的指针域为‘空’

• 更方便的单链表图示：

• 带有头结点的单链表图示：

• 新的空链表图示：

• 单链表的代码：（用结构指针来描述）

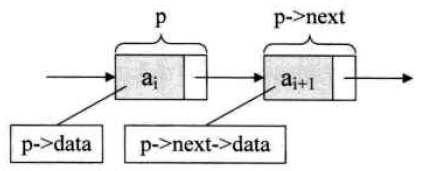
• 结点：由存放数据元素的数据域，和存放后继结点地址的指针域组成。

  • 设p是指向线性表第i个元素的指针，则
  • p->data：其值是一个数据元素，表示结点ai的数据域
  • p->next：其值是一个指针，表示结点ai的指针域，指向第i+1个元素
  • p->data=ai
  • p->next->data=ai+1
  • p和(p->next)都是指针，同等看待

========================================

3.7 单链表的读取

• 相比顺序存储结构的非常容易的读取，要得到单链表的第i个元素，必须从头开始找

• 算法思路：

  • 1-声明一个结点p指向链表第一个结点，初始化j从1开始；
  • 2-当j<i时，就遍历链表，让p的指针向后移动，不断指向下一结点，j累加1；
  • 3-若到链表末尾p为空，则说明第i个元素不存在；
  • 4-否则查找成功，返回结点p的数据。

• 代码实现：

  （ps: 链表L的头结点是L->next？？）

• 时间复杂度：O(n)

  • 最好的情况：i=1时不需要遍历

  • 最坏的情况：i=n时遍历n-1次

  • PS：事先不知道要循环的次数，因此不方便用for循环。while循环也是循环!!!~~

• 核心思想：“工作指针后移”

========================================

3.8 单链表的插入与删除

• 1-单链表的插入

  • 将s结点插入到结点p和p->next之间

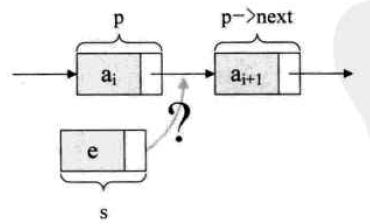
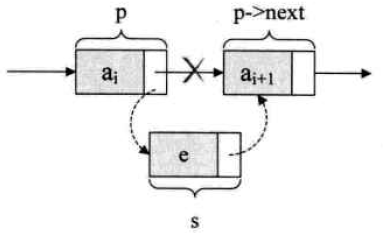
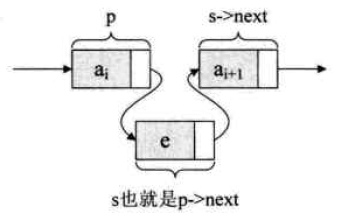
• 操作代码：s->next=p->next; p->next=s;

-- 把p的后继结点改为s的后继结点，再把结点s变成p的后继结点<顺序不可换否则会覆盖p->next的值>

• 单链表的表头和表尾的操作：

• 单链表第i个数据插入结点的算法思路：

  • 1-声明一结点p指向链表第一个结点，初始化j从1开始；
  • 2-当j<i时，就遍历链表，让p的指针向后移动，不断指向下一结点，j累加1；
  • 3-若到链表末尾p为空，则说明第i个元素不存在；
  • 4-否则查找成功，在系统中生成一个空节点s；
  • 5-将数据元素e赋值给s->data；
  • 6-单链表的插入标准语句：s->next=p->next; p->next=s;
  • 7-返回成功。

• 代码实现：

• 2-单链表的删除

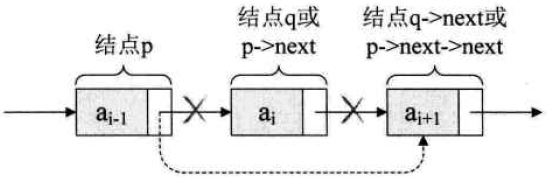
  • 将结点q删除，其中q为存储元素ai的结点。

  • 其实就是将它的前继结点的指针绕过，指向它的后继结点即可。

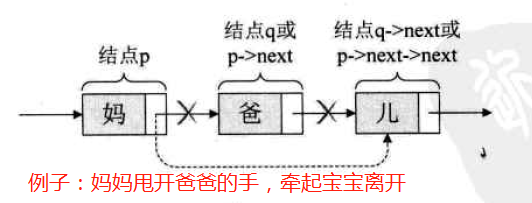
• 操作代码：q=p->next; p->next=q->next; (p->next=p->next->next，用q来取代p->next)

• 单链表第i个数据删除结点的算法思路：

  • 1-声明一结点p指向链表第一个结点，初始化j从1开始；
  • 2-当j<i时，就遍历链表，让p的指针向后移动，不断指向下一个结点，j累加1；
  • 3-若到链表末尾p为空，则说明第i个元素不存在；
  • 4-否则查找成功，将欲删除的结点p->next赋值给q；
  • 5-单链表的删除标准语句：p->next=q->next；
  • 6-将q结点中的数据赋值给e，作为返回；
  • 7-释放q结点；
  • 8-返回成功。

• 代码实现：

• 3-时间复杂度分析

  • 单链表的插入和删除：首先是遍历查找第i个元素，其次是插入和删除操作

  • 故时间复杂度是O(n)

  • 当插入删除一个元素时，与顺序结构比，没有太大优势

  • 但是当从第i个元素的位置插入10个元素时：

    • 顺序结构：每次插入都需要移动元素，每次都是O(n)

    • 单链表：只需要在第一次时，找到第i个位置的指针，此时为O(n)，后面每次都是O(1)

  • 综上，对于插入或删除数据越频繁的操作，单链表的效率优势就越是明显。

========================================

3.9 单链表的整表创建

• 对比顺序结构和单链表的创建：

  • 顺序存储结构的创建：相当于一个数组的初始化，即声明一个类型和大小的数组并赋值的过程。

  • 单链表的创建：动态结构，对于每个链表，它所占空间的大小和位置不需要预先分配划定，可根据需求即时生成。

  • 故：创建单链表：一个动态生成链表的过程，即从“空表”的初始状态起，依次建立各元素结点，并逐个插入链表。

• 单链表整表创建的算法思路：

  • 1-声明一结点p和计数器变量i；
  • 2-初始化一空链表L；
  • 3-让L的头结点的指针指向NULL，即建立一个带头结点的单链表；
  • 4-循环：
    • 生成一新结点赋值给p；
    • 随机生成一数字赋值给p的数据域p->data；
    • 将p插入到头结点与前一新结点之间。

• 头插法：

• 头插法思路：始终让新结点在第一的位置

• 头插法--代码实现：

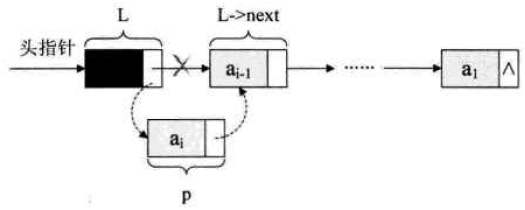
• 注：先把 ( * L ) -> next 赋值给 p 结点的指针域，再把 p 结点赋值给头结点的指针域

  否则会覆盖 ( * L ) -> next

• 头插法--图示：

• 尾插法：

• 尾插法思路：新结点插在终端结点的后面

• 尾插法--代码实现：

  （注：头插法先定义一个头结点，而尾插法不需要头结点）
  
  

• 尾插法--图示：

  • 注：L是指整个单链表，r是指向尾结点的变量，r随着循环不断地变化结点，而L随着循环增长为一个多结点的链表

  
  

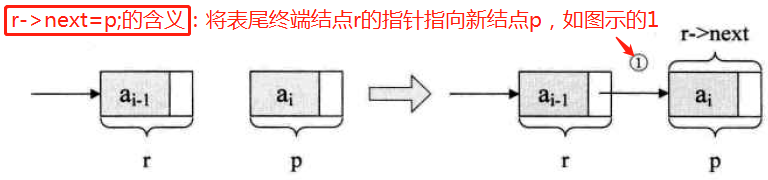
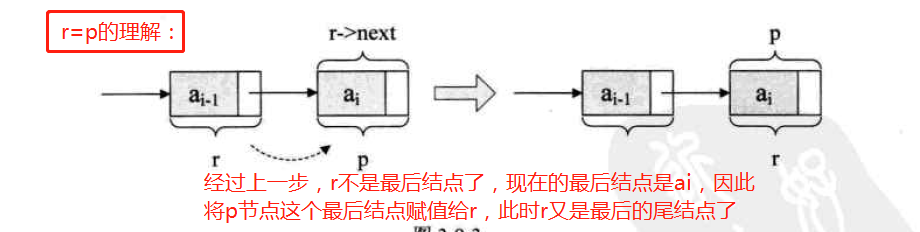
  循环结束后，r->next=NULL--让这个链表的指针域置空。

========================================

3.10 单链表的整表删除

• 单链表整表删除的算法思路：

  • 1-声明一结点p和q；
  • 2-将第一个结点赋值给p；
  • 3-循环；
    • 将下一结点赋值给q；
    • 释放p；
    • 将q赋值给p

• 代码实现：

========================================

3.11 单链表结构与顺序存储结构优缺点

• 简单对比单链表结构和顺序存储结构;

• 对比得出的一些经验性的结论：

  • 1-若线性表多查找，少插删，宜采用顺序存储结构；若多查删，宜采用单链表结构

  举例：游戏开发中，用户注册信息时，除了注册时插入，其他时候多读取，用顺序；而玩家的装备随时增删，用单链表。

  • 2-若线性表的元素个数变化大或不确定时，宜采用单链表；若确定或事先明确个数，用顺序存储效率更高。

  • 3-总结：各有优缺点，不能简单说哪个好哪个不好，需要根据实际情况综合分析哪种更合适。

========================================

3.12 静态链表

• 引入：

  • 1-出现问题：c有指针，而有些面向对象语言如java、c#等启用了对象引用机制，间接实现了指针的作用；而有些语言如basic等没有指针，如何实现链表结构呢？
  • 2-解决思路：用数组代替指针，来描述单链表

• 定义：用数组描述的链表叫做静态链表，或曰“游标实现法”。

  • 数组的元素都是由两个数据域组成的，data（数据）和cur（游标）

  • 即数组的每个下标都对应一个data和一个cur

    • 数据域data：用来存放数据元素，也就是我们要处理的数据。
    • 游标cur：相当于单链表中的next指针，存放该元素的后继在数组中的下标。
    • 注：此处的游标cur不是数组的索引，而是数组索引之外的又一个值

  
  

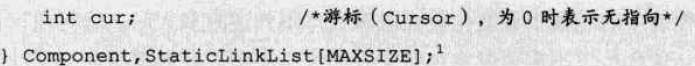
  • 备用链表：通常把未被使用的数组元素称为备用链表。（即数组的后面还没填充数据的空闲空间）

  • 对于数组特殊元素的设置：

  

  • 上图示此时相当于初始化的数组状态。对应的代码实现：

  

  • 将数据存入后的状态：

  
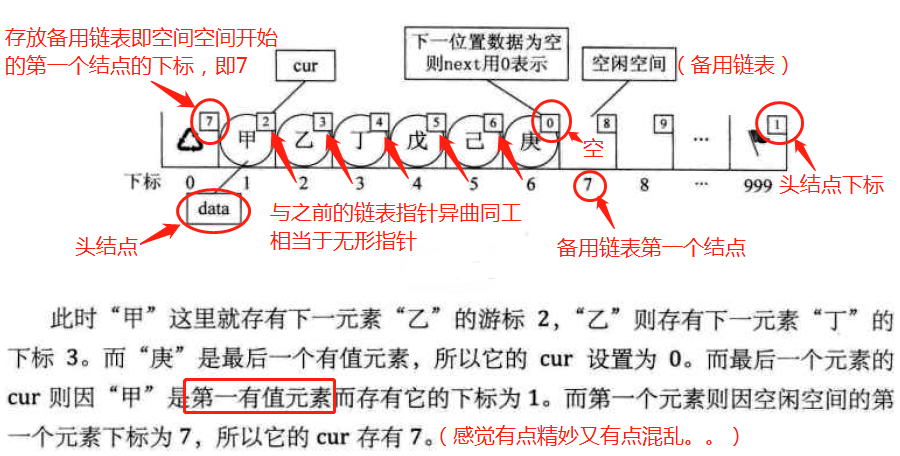
  （注，左上角笔误：空闲空间，不是空间空间。。还有图中标记的所谓“头结点”存疑，可以说是开始结点）

• 1-静态链表的插入操作

• 动态链表中：结点的申请和释放分别借用函数malloc()和free()来实现

• 静态链表中：操作的是数组，需要自己实现这两个函数，以便进行插删操作

• malloc()函数的静态链表代码实现：（配合上图食用效果更佳）

• 静态链表插入操作的代码实现

• 静态链表插入操作的图示：（在乙和丁之间插入丙，只需改变乙和丙的cur即可）

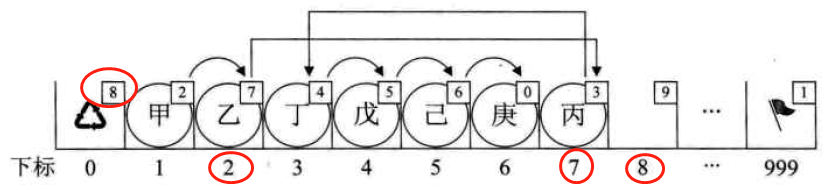
• 2-静态链表的删除操作

• free()函数的静态链表代码实现：

• 静态链表删除操作的代码实现：

• 静态链表删除操作的图示：（）

• 3-静态链表优缺点

========================================

3.13 循环链表

• 循环链表（circular linked list）的定义：

  • 将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成了一个环

  • 这种头尾相接的单链表称为单循环链表，简称循环链表

• 优势：

  解决了一个问题：即如何从当中一个结点出发，访问到链表的全部结点。

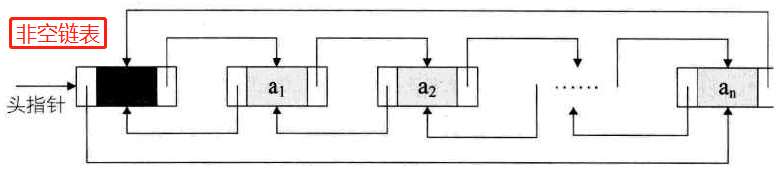
• 带有头结点的循环链表图示-空链表和非空链表

• 循环链表和单链表的差异：循环的判断条件

  • 单链表：判断p->next是否为空

  • 循环链表：判断p->next不等于头结点，则循环未结束

• 尾指针rear

  • 引入： 有头结点时，访问第一个结点用 O(1)，但访问最后一个结点用O(n)

  • 有了尾指针以后，访问第一个结点和最后一个结点的时间均为O(1)了

    • 尾指针：rear
    • 头指针：rear->next

  • 尾指针图示：

• 示例：将两个循环链表合并成一个表时：

  • 图示：

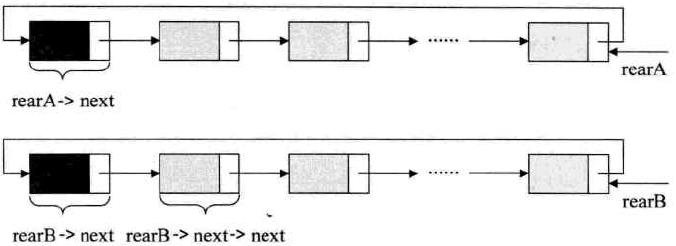
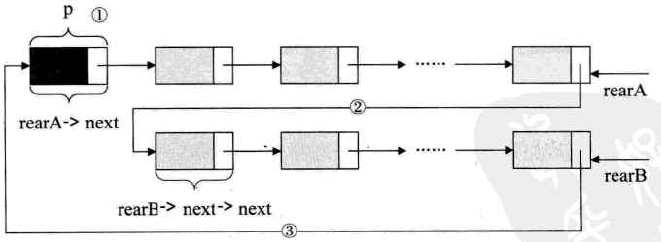
• 代码实现：

========================================

3.14 双向链表

• 双向链表（double linked list）的定义：

  在单链表的每个结点中，再设置一个指向其前驱结点的指针域

  即在双向链表中的结点都有两个指针域，一个指向直接后继，一个指向直接前驱

• 代码实现：

• 带有头结点的双向链表的图示：空链表和非空链表

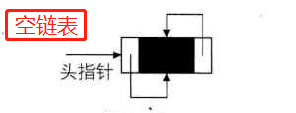
• 双向链表的前驱的后继：它自己

  • p->next>prior = p = p->prior->next

• 双向链表的插入操作：

  注意顺序：先s的前驱和后继，再后结点的前驱，最后前结点的后继

• 双向链表的删除操作：

• 好处和弊端分析

  • 弊端：在插入删除时，需要更改两个指针变量，并且占用更多空间

  • 好处：良好的对称性，有效提高算法的时间性能

  • 综上：用空间换时间

========================================

3.15 总结回顾

========================================

3.16 结尾语

END