【学习总结】《大话数据结构》- 第2章-算法

【学习总结】《大话数据结构》- 总

启示：

  • 算法：解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

目录

========================================

2.1 开场白

  • 一些可以略过的场面话...

========================================

2.2 数据结构与算法关系

  • 举例独角戏《梁山伯》、《罗密欧》类比数据结构和算法的亲密关系
  • 本课程以数据结构为主，算法为辅

========================================

2.3 两种算法的比较

  • 举例求1+2+3+...+100的两种方法

    • 1-for循环：sum = sum+i
    • 2-小高斯公式法：sum = (1+n)*n / 2

  • 重点在于：数值小时差不多，数值很大、巨大时，for循环就显得很慢很重了。。

========================================

2.4 算法定义

  • 算法（Algorithm）这个单词最早出现在波斯数学家阿勒·花刺子密的公元825年《印度数字算术》中

  • 算法：

    解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

    • 指令：能被人或计算机等计算装置执行。可以是计算机指令，也可以是语言文字。

    • 需要把指令表示成一定的操作序列。操作序列包括一组操作，每个操作都完成特定的功能。这就是算法了。

  • 不同问题，对应不同算法。相当于不同的病症，对应不同的药方。

========================================

2.5 算法特性

  • 五个特性：输入、输出、有穷性、确定性、可行性。

  • 1-输入输出：

    • 可以有0个或多个输入，至少有一个或多个输出。

    • 输出：可以是打印，或者返回一个或多个值，等。

（没有输出的算法，是没有意义的，相当于做了无用功，所以至少有一个输出，即返回值，或运行后导致了某些改变）

  • 2-有穷性：

    • 定义：算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。

    • 注：‘有穷’：不是纯数学意义的，而是在实际应用中合理的、可接受的'有边界'

（例子：一个算法，需要运行二十年，这是数学意义的有穷的，但是现实意义不大了）

  • 3-确定性：

    • 定义：算法的每一步骤都具有确定的含义，不会出现二义性。

    • 具体地：一定条件下，只有一条执行路径，相同输入只能有唯一的输出结果，每个步骤都被精确定义而无歧义。

  • 4-可行性：

    • 定义：每一步都必须是可行的，即每一步都能够通过执行有限次数完成。

    • 具体地：可行性意味着算法可以转换为程序上机运行，并得到正确的结果。

========================================

2.6 算法设计的要求

  • 要求：正确性、可读性、健壮性、时间效率高和存储量低、

  • 1-正确性：

    • 定义：算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。

  • 2-可读性：

    • 定义：算法设计的另一目的是为了便于阅读、理解和交流。

    • 可读性是算法（包括实现它的代码）好坏的很重要的标志。

  • 3-健壮性：

    • 定义：当输入数据不合法时，算法也能做出相关处理，而不是产生异常或莫名其妙的结果。

  • 4-时间效率高和存储量低

    • 考虑时间复杂度和空间复杂度的问题

    • 用最少的存储空间，花最少的时间，办成同样的事，就是好的算法。

========================================

2.7 算法效率的度量方法

  • 1-事后统计方法：

    • 主要是通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低。

    • 这种方法具有很大缺陷，比如需要事先编制程序、时间依赖硬件和软件，测试数据设计困难等

    • 故不予采纳本方法

  • 2-事前分析估算方法

    • 定义：在计算机程序编制前，依据统计方法对算法进行估算。

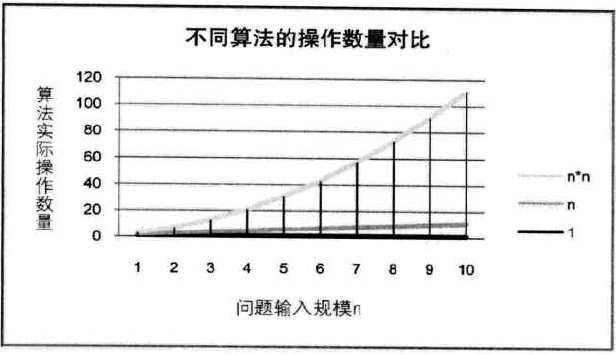
  • 一个程序的运行时间：(抛开硬件、软件因素)，依赖于算法的好坏和问题的输入规模。输入规模即输入量的多少。

  • 求和的两个方法的对比：

  • 另一个双层for循环的例子：

  • 故：测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数。

  • 分析一个算法的运行时间时，要把基本操作的数量与输入规模关联起来，即基本操作的数量必须表示成输入规模的函数。

========================================

2.8 函数的渐近增长

  • 定义：

  • 判断一个算法的效率时，函数中的常数和其他次要项可以忽略，而更应该关注主项（最高阶项）的阶数。

========================================

2.9 算法时间复杂度

  • 1-定义：

    • 在进行算法分析时，语句总的执行次数 T(n) 是关于问题规模n的函数，进而分析 T(n) 随n的变化情况并确定 T(n) 的数量级。算法的时间复杂度，也就是算法的时间度量，记作：T(n) = O(f(n))，表示随问题规模n的增大，算法执行时间的增长率和 f(n) 的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中 f(n) 是问题规模n的某个函数。

    • 大O记法：用大写 O() 来体现算法时间复杂度的记法。

    • 随着n的增大，T(n)增长最慢的算法为最优算法。

    • 常见时间复杂度的非官方名称：O(1)-常数阶，O(n)-线性阶，O(n^2)-平方阶

  • 2-推导大O阶方法

    • 攻略：

  • 3-常数阶

    • 口诀'1'：用常数1取代运行时间中的所有加法常数。

    • 注意：不管常数是多少，均记作O(1)

    • 另：分支结构(if结构，switch语句)--无论真假，执行次数恒定，故也是常数阶。

    • 栗子一枚：

  • 4-线性阶

    • 关键：分析循环结构的运行情况

    • 栗子一枚：

  • 5-对数阶

    • 关键：当循环体中有加快循环的语句时

    • 栗子一枚：

  • 6-平方阶

    • 关键：循环的时间复杂度=循环体的复杂度*该循环运行次数（嵌套for时）

    • 例子：


========================================

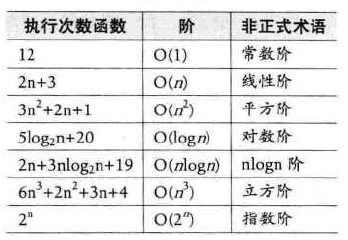
2.10 常见的时间复杂度

  • 表格总结：

  • 不同时间复杂度的时间耗费排序：

    • O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O<(nn)

========================================

2.11 最坏情况与平均情况

  • 时间复杂度的两种常见类型：

    • 平均时间复杂度（最有意义的，是期望的运行时间）

    • 最坏时间复杂度（最重要的，一种保证，运行时间不会再坏了）

  • 一般没有特殊说明的情况下，默认是最坏时间复杂度

========================================

2.12 算法空间复杂度

  • 空间复杂度：

    • 通过计算算法所需的存储空间实现

  • 计算公式：

    • S(n) = O(f(n)) - 也用大O表示

  • 通常以时间复杂度为重，不用限定词时默认为时间复杂度。

========================================

2.13 总结回顾

  • 算法的定义：解决特定问题求解步骤的描述，在计算机中为指令的有限序列，并且每条指令表示一个或多个操作。

  • 算法的特性：有穷性、确定性、可行性、输入、输出。

  • 算法的设计要求：正确性、可读性、健壮性、高效率和低存储量需求。

  • 算法的度量方法：事后统计方法（不科学不准确）和事前分析估算方法。

  • 函数的渐近增长

  • 推导大O的步骤（123）

  • 常见时间复杂度耗时排序

========================================

2.14 结尾语

END

posted @ 2019-05-08 14:15  anliux  阅读(930)  评论(0)  编辑  收藏  举报