数据结构之快速排序
1.快速排序是对冒泡排序的一种改进，是所有内部排序算法中平均性能最优的排序算法
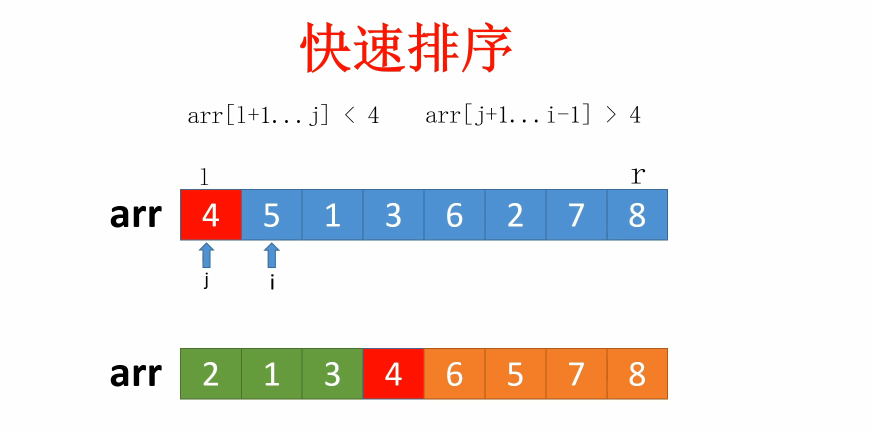
首先我们要先找一个基准值4，让在4左边的都是小于4的数，在4右边的都是大于4的数。比如下面arr数组中索引在l到j之间的都是小于4的，索引在j+1到i-1之间都是大于4的。
如果想要让整个数组都变成有序的，那就需要进行递归，对各个区间中的数据分别做快速排序，直到数据有序。
代码实现：
class QuickSort { public static void Sort(int[] arr) { Sort(arr, 0, arr.Length - 1); } private static void Sort(int[] arr, int l, int r) { if (r - l + 1 <= 15) { //也可以直接返回，或者使用直接插入排序 InsertSort(arr, l, r); return; } //基准值 int v = arr[l]; int j = l; for (int i = l + 1; i <= r; i++) { //如果当前值小于基准值v，要先j++，，然后交换，确保基准值左侧都是小于它的数; if (arr[i] < v) { j++; Swap(arr, i, j); } } //将基准值放到符合左右2侧分别小于大于它的地方 Swap(arr, l, j); //使用递归分别对基准值左右2侧的数据进行快速排序 Sort(arr, l, j - 1);//左侧 Sort(arr, j + 1, r);//右侧 } /// <summary> /// 元素交换 /// </summary> /// <param name="arr"></param> /// <param name="i"></param> /// <param name="j"></param> private static void Swap(int[] arr, int i, int j) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } /// <summary> /// 插入排序 升序 /// </summary> /// <param name="arr"></param> public static void InsertSort(int[] arr, int l, int r) { for (int i = l + 1; i <= r; i++) { //插入元素e int e = arr[i]; //j表示元素e应该插入的位置 int j; for (j = i; j > 0; j--) { if (e < arr[j]) { arr[j] = arr[j - 1]; } else { //此时说明不用再比较了 break; } } //通过for循环判断，最终找到了j具体的位置，将元素e放在此位置上 arr[j] = e; } } }
随机化快速排序
但是当数组处于一种近乎有序的情况下，便会非常慢，因为之前我们都是默认第一个元素为基准元素
代码更改（具体）：
class QuickSort { private static Random random; public static void Sort(int[] arr) { Sort(arr, 0, arr.Length - 1); } private static void Sort(int[] arr, int l, int r) { if (r - l + 1 <= 15) { //也可以直接返回，或者使用直接插入排序 InsertSort(arr, l, r); return; } //基准值 int p = l + random.Next(r - l + 1);//随机的基准值索引 Swap(arr, l, p); int v = arr[l]; int j = l; for (int i = l + 1; i <= r; i++) { //如果当前值小于基准值v，要先j++，，然后交换，确保基准值左侧都是小于它的数; if (arr[i] < v) { j++; Swap(arr, i, j); } } //将基准值放到符合左右2侧分别小于大于它的地方 Swap(arr, l, j); //使用递归分别对基准值左右2侧的数据进行快速排序 Sort(arr, l, j - 1);//左侧 Sort(arr, j + 1, r);//右侧 } /// <summary> /// 元素交换 /// </summary> /// <param name="arr"></param> /// <param name="i"></param> /// <param name="j"></param> private static void Swap(int[] arr, int i, int j) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } /// <summary> /// 插入排序 升序 /// </summary> /// <param name="arr"></param> public static void InsertSort(int[] arr, int l, int r) { for (int i = l + 1; i <= r; i++) { //插入元素e int e = arr[i]; //j表示元素e应该插入的位置 int j; for (j = i; j > 0; j--) { if (e < arr[j]) { arr[j] = arr[j - 1]; } else { //此时说明不用再比较了 break; } } //通过for循环判断，最终找到了j具体的位置，将元素e放在此位置上 arr[j] = e; } } }
三向切分的快速排序方法
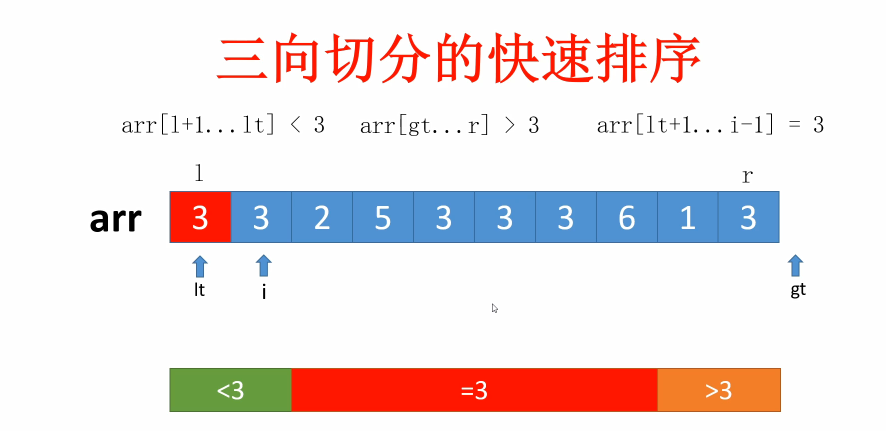
还有一种情况是存在大量重复元素，这也会导致性能降低，甚至栈溢出。所以我们可以通过三向切分的方法来解决，将数组分为三部分：小于当前切分元素的部分，等于当前切分元素的部分，大于当前切分元素的部分。如下用不同颜色区分的展示情况：
代码实现:
/// <summary> /// 三向切分的快速排序类 /// </summary> class QuickSort3 { private static Random random; public static void Sort(int[] arr) { Sort(arr, 0, arr.Length - 1); } private static void Sort(int[] arr, int l, int r) { //（1）如果数组量不大，可以直接用插入排序 if (r - l + 1 <= 15) { //也可以直接返回，或者使用直接插入排序 InsertSort(arr, l, r); return; } //基准值（2）防止出现近乎有序的数组，使用随机索引值 int p = l + random.Next(r - l + 1);//随机的基准值索引 Swap(arr, l, p); int v = arr[l]; int lt = l;//当前数组区域的开始索引 int gt = r + 1;//当前数组区域的最大索引值加1 int i = l + 1;//定义i，用它指向遍历的每一个元素 while (i < gt) { if (arr[i] < v) { //之所以要先递增lt，是因为现在lt指向的数据是 //默认比基准值小的数，所以要前进一步，否则更换就没意义了。 lt++; Swap(arr, i, lt); i++; } else if (arr[i] > v) { gt--; Swap(arr, i, gt); } else { i++; } } //此时要 Swap(arr, l, lt); //使用递归进行快速排序 Sort(arr, l, lt - 1);//左侧 Sort(arr, gt, r);//右侧 } /// <summary> /// 元素交换 /// </summary> /// <param name="arr"></param> /// <param name="i"></param> /// <param name="j"></param> private static void Swap(int[] arr, int i, int j) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } /// <summary> /// 插入排序 升序 /// </summary> /// <param name="arr"></param> public static void InsertSort(int[] arr, int l, int r) { for (int i = l + 1; i <= r; i++) { //插入元素e int e = arr[i]; //j表示元素e应该插入的位置 int j; for (j = i; j > 0; j--) { if (e < arr[j]) { arr[j] = arr[j - 1]; } else { //此时说明不用再比较了 break; } } //通过for循环判断，最终找到了j具体的位置，将元素e放在此位置上 arr[j] = e; } } }
总结：
设置一个基准值，这个基准值最好是随机的，然后将整个无序表分成3个区间，一个区间是存放小于基准值的，一个是等于基准值，一个是大于基准值的，然后再对各个区间做快速排序处理，知道整个数组有序
