【学习笔记】最小生成树与最短路

最小生成树与最短路

注意：本文中列出的所有“解释”有可能不是该算法的严格数学证明

I 概念

对于一个连通带权图 $G = (V, E)$，我们称包含所有点的一个连通树子图为其一个生成树，即 $H = (V', E'),\ V' = V, E'\subseteq E, \vert E' \vert = \vert V' \vert - 1 $；所有生成树中边权最小的为其最小生成树(MST)。

对于一个连通带权图 $G = (V, E)$，我们称对于 $u,v\in V$，从 $u$ 到 $v$ 的一条没有重复点的链为其一个简单路径；所有 $u$ 到 $v$ 的简单路径中边权和最小的为其最短路。

II 最小生成树

1. Kruskal （贪心加边）

方法： 从按边权从小到大加入边，如果该边两点已经连通，那么就不加这条边。先对边进行排序，加边时使用并查集维护连通性。

解释： 在这个过程中，每次加边实质就是取消了该边连接的两个连通分量间的连通性。如果加边 $e$ 后成环，那么该边两点已经连通，由于贪心过程，该边两点所在的连通分量中所有边的边权一定严格不大于该边边权，换句话说，加入该边一定不优。如此来看，如果贪心地加边，那么必然能够保证最优地维护连通性，生成最小生成树。

复杂度： 对于一个有 $n$ 个点和 $m$ 条边的连通图，首先对边进行 $O(m \log m)$ 的排序， $m$ 次加边每次进行 $O(\log m)$ 的并查集维护连通性。总的复杂度就是 $O(m \log m)$。

代码：

// 本代码输出最小生成树的边权之和
#include<bits/stdc++.h>
#define MAXN 400010
using namespace std;
int ltp;
int fa[MAXN], vis[MAXN], n, m, ans, cnt;
struct nds{
    int x, y, w;
}e[MAXN];
void add(int x,int y,int w)
{
    e[++ltp] = {x, y, w};
}
int find(int x)
{
    if(fa[x] == x) return fa[x];
    else fa[x] = find(fa[x]);
    return fa[x];
}
bool cmp(nds a,nds b)
{
    return a.w < b.w;
}
void Kruskal()
{
    sort(e + 1, e + 1 + m, cmp);
    for(int i = 1; i <= n;i++)
        fa[i] = i;
    for(int i = 1; i <= m;i++){
        int fx = find(e[i].x), fy = find(e[i].y);
        if(fx == fy) continue;
        ans += e[i].w;
        fa[fx] = fy;
        if(++cnt == n - 1) break;
    }
    printf("%d", ans);
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m;i++){
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w);
    }
    Kruskal();
    return 0;
}

2. Prim （贪心加点）

方法： 对于连通带权图 $G = (V, E)$，维护一个已加点的点集 $V_{new} \subseteq V$：每次对于已加点的点集 $V_{new}$，找出边权最小的边 $(u, v) \in E$，且 $u \in V_{new}，v\notin V_{new}$，并将 $v$ 加入点集 $V_{new}$ 中。重复该操作，直到 $V_{new} = V$。

解释： 考虑任意最小生成树的子树，发现在贪心过程中该子树在一个一个添加结点的过程中保证了边权和最小。即对于任意的子树，对于每个结点，在加入该子树时都是与边权最短的结点相连接的，故而能保证最优。

复杂度： 对于一个 $n$ 个点 $m$ 条边的图，共要进行 $n$ 次加点操作，每次加点操作都需要 $n$ 次暴力找出该点集距离最近的点，故而复杂度为 $O(n^2)$。

代码：

// 本代码输出最小生成树的边权之和
#include<bits/stdc++.h>
#define MAXN 400010
#define INF 0x3f3f3f3f
using namespace std;
int lk[MAXN], ltp;
struct nds{
    int nxt, y, w;
} e[MAXN];
void add(int x,int y,int w)
{
    e[++ltp] = {lk[x], y, w};
    lk[x] = ltp;
}
int n, m, ans, tot, now = 1, vis[MAXN], dist[MAXN];
int Prim(){
    for(int i = 2; i <= n; i++) 
        dist[i] = INF;
    for(int i = lk[1]; i; i = e[i].nxt) 
        dist[e[i].y] = min(dist[e[i].y], e[i].w);
    while(++tot < n){
        vis[now] = 1;
        int minn = INF;
        for(int i = 1; i <= n; i++)
            if (!vis[i] && minn > dist[i])
                minn = dist[i], now = i; //找出此时最短的(u,v)，并加点
        ans += minn;
        for(int i = lk[now]; i; i = e[i].nxt){ // 加点后更新 (u, v)
            int y = e[i].y;
            if(dist[y] > e[i].w && !vis[y])
                dist[y] = e[i].w;
        }
    }
    printf("%d", ans);
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++){
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w);
        add(y, x, w);
    }
    Prim();
    return 0;
}

III 最短路

0.最短路的一些基础知识

以下均讨论一个 $n$ 结点和 $m$ 条边的带权连通图 $G = (V, E)$。同时当前所求单源最短路的源节点为 $s$，终点为 $v$。

我们记边 $(u,v)$ 的边权为 $w_{(u,v)}$，记 $\mathrm{dis}(u, v)$ 为当前状态下点 $u$ 到 $v$ 的最短路的长度，记 $\mathrm{D}(u, v)$ 为最终状态下点 $u$ 到 $v$ 的实际最短路的长度。

我们用“ $a\rightsquigarrow b$ ”表示一条从 $a$ 到 $b$ 的可能经过别的点的路径（或是没有任何边的空路径），用“ $a \rightarrow b$ ”表示一条直接连接 $a$ 到 $b$ 的边。

最短路的长度： 显然，最短路上不可能存在着权值和为正数的环路，因为最短路完全可以不走这条环路。如果存在着权值和为负数的环路，那么最短路可以经过无限次这条环路，使得最短路的总权值和为 $-\infin$。故而我们不允许负环的存在。综上，我们可以发现，由于没有环的存在，最短路最多拥有着 $n - 1$ 条边。

最短路的子路径仍是最短路： 设 $s$ 到 $v$ 的最短路为 $s \rightsquigarrow u \rightsquigarrow v$，则该最短路的子路径 $s \rightsquigarrow u$ 和 $u \rightsquigarrow v$ 分别是 $s$ 到 $u$ 和 $u$ 到 $v$ 的最短路。（因为如果不是最短，那么总的最短路还能更短）。

上界性质： 一般地，我们总有

\[\mathrm{dis}(s,u) \geqslant\mathrm{D}(s,u) \]

三角不等式性质： 一般地，我们总有

\[D(s,v) \leqslant\mathrm{D}(s,u) + w_{(u,v)} \]

松弛操作： 在当前状态下对最短路的更新操作。对于需求最短路 $\mathrm{dis}(s, v)$，我们对边 $(u,v)$ 进行松弛操作，即通过该边更新源点 $s$ 到结点 $v$ 的最短路，使 $$\mathrm{dis}(s,v)=\min(\mathrm{dis}(s,v),\ \ \mathrm{dis}(s,u)+\mathrm{dis}(u,v))$$

1.Bellman-Ford 求带负权的单源最短路

一个视频例子，~~请注意流量~~

方法： 总共循环 $n$ 次，每次循环内遍历所有边，并对每条边 $(u,v)$ 进行松弛操作，更新 $\mathrm{dis}(s, v)$。如果第 $n$ 次遍历后还能进行松弛操作，那么判定该图内有负环，不存在最短路。如果该轮无法进行松弛操作，说明已找到了最短路。

解释： 注意到，对 $(u, v)$ 的松弛操作的实质就是试图建立一条 $s \rightsquigarrow u \rightarrow v$ 的最短路径，而每一次松弛操作，这条路径就会多一条`边。换句话说，在第 $k$ 轮对所有边进行松弛操作时，这轮松弛的边就将最多是最短路的第 $k$ 条边，而 $s\rightsquigarrow u$ 就最多有 $k - 1$ 条边（因为有可能 $s \rightsquigarrow u$ 不是上一轮松弛得来的）。以此类推，由于最短路最多拥有 $n - 1$ 条边，故而在第 $n$ 轮操作中不可能进行松弛操作，如果能进行，则必然存在负环。

由于要进行松弛操作，所以要把所有 $\mathrm{dis}(s,u)$ 初始化为 $\infin$。

\[\color{red}\text{关于SPFA，它死了} \]

~~所以我们不说SPFA，它没什么卵用~~

时间复杂度： 最多进行 $n$ 轮松弛操作，每次最多松弛 $m$ 条边，故时间复杂度为 $O(nm)$。

代码：

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define MAXN 40010
using namespace std;
int lk[MAXN], ltp;
struct nds{
    int y, nxt, w;
}e[MAXN];
void add(int x, int y, int w)
{
    e[++ltp] = {y, lk[x], nxt};
    lk[x] = ltp;
}
int n, m, s, dist[MAXN];
void BellmanFord()
{
    bool flag; // flag 判定是否进行了松弛操作
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    for(int i = 1; i <= n; i++){
        flag = false;
        for(int u = 1; u <= n; u++){
            if(dist[u] == INF) continue;
            for(int ed = lk[u]; ed; ed = e[ed].nxt){
                int edy = e[ed].y, edw = e[ed].w;
                if(dist[y] > dist[u] + edw){
                    flag = true;
                    dist[y] = dist[u] + edw;
                }
            }
        }
        if(i == n && flag == true) ans = -1; // ans = -1 说明有负环
    }
    for(int i = 1; i <= n; i++)
        printf("%d ", dist[i]);
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &s);
    for(int i = 1; i <= m; i++) {
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w);
    }
    BellmanFord();
    return 0;
}

2.Dijkstra 求带正权的单源最短路

一个视频例子，~~请注意流量~~

方法：
和Prim算法有相似之处。首先维护一个点集 $V_{new}$，初始为空。每次选择一个 $\mathrm{dis}(s,u)$ 最小的结点 $u$ 加入到点集 $V_{new}$ 中，并对所有 $u$ 的出边进行松弛操作。加点直到 $V_{new} = V$。在维护最小距离的结点时，可以遍历所有点的 $dis$ 值，也可以使用堆优化。

解释：
这个算法的神奇之处在于：当将结点 $u$ 加入到点集 $V_{new}$ 中时， $\mathrm{dis}(s, u) =\mathrm{D}(s, u)$，即已经求出了 $s$ 到 $u$ 的最短路。解释了这一点就解释了整个算法。

我们假设即将加入（还未加入）的 $u$ 为第一个使 $\mathrm{dis}(s,u) \ne\mathrm{D}(s,u)$ 的结点（因为 $s$ 结点必然成立，所以 $u \ne s$）。同时令 $s$ 到 $u$ 实际的最短路径为 $s \rightsquigarrow x \rightarrow y \rightsquigarrow u$，其中 $x \in V_{new}, \ y \notin V_{new}$，但 $x$ 有可能等于 $s$，$y$ 有可能等于 $u$。

因为 $u$ 是第一个使 $\mathrm{dis}(s,u) \ne\mathrm{D}(s,u)$ 不成立的结点，故而 $x$ 结点满足 $\mathrm{dis}(s,x) =\mathrm{D}(s,x)$。同时因为最短路的子路径都是最短路，我们知道 $x$ 到 $y$ 的最短路即为 $x \rightarrow y$，故而在此之后边 $(x,y)$ 肯定经过了松弛操作，从而此时 $\mathrm{dis}(s,y) =\mathrm{D}(s,y)$。
因为所有权值非负，故而 $\mathrm{D}(s,u) \geqslant \mathrm{D}(s,y)$。故而 $\mathrm{dis}(s,y) =\mathrm{D}(s,y) \leqslant\mathrm{D}(s,u) \leqslant \mathrm{dis}(s,u)$。根据算法内容，此时添加的结点 $u $为 $V_{new}$ 外 $\mathrm{dis}$ 最小的结点，但是此时 $y$ 的 $\mathrm{dis}$ 更小，矛盾，故而 $u$ 不是第一个使 $\mathrm{dis}(s,u) \ne\mathrm{D}(s,u)$ 的结点，由于有源点 $s$ 的存在，故而 $u$ 只能使得 $\mathrm{dis}(s,u) = \mathrm{D}(s,u)$。

时间复杂度：

不加优化，每次暴力枚举所有 $n$ 的 $\mathrm{dis}$，那么复杂度是 $O(n^2)$。
加入堆优化（优先队列），那么实质是在每次松弛操作后都会将更新的结点加入堆中，保证每次加点时的最小 $\mathrm{dis}$ 都是堆顶元素。但是每次松弛边操作加入的点可能重复，堆内最多有 $m$ 个元素，每个元素弹出需要 $O(\log m)$ 的时间（当然，因为 $O(\log m) = O(\log n)$，所以两者皆行）。每个元素都有弹出一次（尽管可能不会加入到点集中），故总的复杂度为 $O(m \log n)$。

代码：

// 不加堆优化的朴素算法
#include<bits/stdc++.h>
#define MAXN 100010
#define INF 0x3f3f3f3f
using namespace std;
int lk[MAXN], ltp;
struct nds{
    int nxt, y, w;
}e[MAXN];
void add(int x,int y,int w)
{
    e[++ltp] = {lk[x], y, w};
    lk[x] = ltp;
}
int n, m, s, dist[MAXN], vis[MAXN];
void Dijkstra()
{
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    for(int i = 1; i <= n; i++){
        int tmp = 0, tdis = INF;
        for(int j = 1; j <= n; j++)
            if(!vis[j] && dist[j] < tdis)
                tmp = j, tdis = dist[j];
        vis[tmp] = true;
        for(int ed = lk[tmp]; ed; ed = e[ed].nxt){
            int edy = e[ed].y, edw = e[ed].w;
            if(dist[tmp] + edw < dist[edy])
                dist[edy] = dist[tmp] + edw;
        }
    }
    for(int i = 1; i <= n; i++)
        printf("%d ", dist[i]);
}
int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i <= m;i++){
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w);
    }
    Dijkstra();
    return 0;
}

// 堆（优先队列）优化的算法
#include<bits/stdc++.h>
#define MAXN 100010
#define INF 0x3f3f3f3f
using namespace std;
int lk[MAXN], ltp;
struct nds{
    int nxt, y, w;
}e[MAXN];
void add(int x,int y,int w)
{
    e[++ltp] = {lk[x], y, w};
    lk[x] = ltp;
}
struct Node{
    int d, p;
    bool operator <(const Node &x)const{
        return x.d < d;
    }
}; // 优先队列排序需要的数据结构
priority_queue<Node> q;
int n, m, s, dist[MAXN], vis[MAXN];
void Dijkstra()
{
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    q.push((Node){0, s});
    while(!q.empty()){
        Node tmp = q.top();
        q.pop();
        if(vis[tmp.p]) continue;
        vis[tmp.p] = false;
        for (int ed = lk[tmp.p]; ed; ed = e[ed].nxt){
            int edy = e[ed].y, edw = e[ed].w;
            if(dist[tmp.p] + edw < dist[edy]){
                dist[edy] = dist[tmp.p] + edw;
                if(!vis[edy])
                    q.push({dist[edy], edy});
            }
        }
    }
    for(int i = 1; i <= n; i++)
        printf("%d ", dist[i]);
}
int main()
{
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i <= m;i++){
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        add(x, y, w);
    }
    Dijkstra();
    return 0;
}

3.Floyd 求带正权的全源最短路

方法： 我们考虑 DP 处理。对于所有 $i, j\in V$，和所有 $k \leqslant n$，我们定义数组 $d[k][i][j]$ 为从 $i$ 结点到 $j$ 结点路径中只经过 $1 \sim k$ 中的结点（或者根本不经过结点）的最短路长度。我们有状态转移方程：

\[\begin{aligned}d[k][i][j]= \begin{cases} w_{(i,j)}&(k=0) \\ \min(d[k-1][i][j]，d[k-1][i][k] + d[k-1][k][j]&(0<k\leqslant n) \end{cases}\end{aligned}\]

特别的，在实际代码中，实际的数组可以不写第一维。

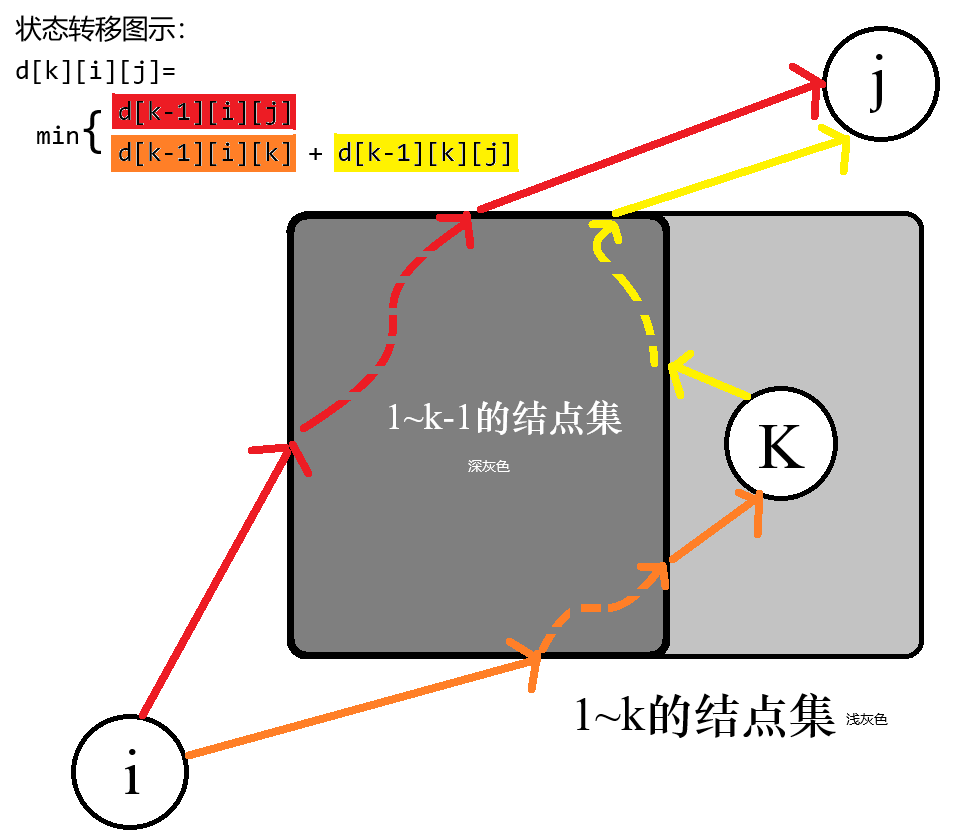
解释： 实质上，该算法的目的就是不断扩充点集 $V_{new} = \{1,2,\cdots,k\}$，每次都求出所有 $i,j$ 间只经过点集 $V_{new}$ 的最短路 $\mathrm{dis}(i,j)$。当 $V_{new} = V$ 时，此状态下的 $\mathrm{dis}(i,j)$ 实质上就等于 $\mathrm{D}(i,j)$。

递归地，我们设当前已知了所有 $d[k-1][i][j]$ 的值，即知道了所有只经过结点集 $V_{new} = \{1,2,\cdots,k-1\}$ 中的结点的最短路。现在我们想要求出如果将点 $k$ 加入到 $V_{new}$ 后，$d[k][i][j]$ 的数值。观察上图，我们发现，新的 $i$ 到 $j$ 只经过新的 $V_{new}$ 的最短路径，无非是原先的红色路径（$d[k-1][i][j]$），或者是橙色路径（$d[k-1][i][k]$）与黄色路径（$d[k-1][k][j]$）拼起来。二者中小的就是最短路。

为了保证每次都已知 $d[k-1][i][j]$ 的值，我们就要在最外层循环 $k$。否则很有可能在枚举 $d[k][i][j]$ 时，所谓的 $d[k-1][i][k]$ 等不是当前最短的。

在每次外层循环 $k$ 固定时，我们根据上图，不难发现都有 $d[k][i][k] = d[k-1][i][k]，d[k][k][j] = d[k-1][k][j]$。如果我们取消掉数组的第一维，实质就是直接让 $d[k][i][j]$ 覆盖掉 $d[k-1][i][j]$。如果 $i = k$ 或者 $j = k$，根据前面两式相等的结论，这个覆盖不会产生任何改变。如果 $i\ne k，j \ne k$，那么由于在所有当前第 $k$ 轮循环中，不会有其他任何状态使用这个 $d[i][j]$（即不会根据这个更新自己），故而可以放心覆盖掉。由此，数组的第一维即可抛弃。

时间复杂度： $k$ 轮循环，每轮循环出所有点对 $(i,j)$，故复杂度为 $O(n^3)$，但常数较小。

代码：

// 本代码中所求出的所有多源最短路存放在 dis[u][v] 数组中
#include<bits/stdc++.h>
#define MAXN 1000
#define INF 0x3f3f3f3f
using namespace std;
int n, m, dis[MAXN][MAXN];
void Floyd()
{
    for(int k = 1; k <= n; k++)
        for(int u = 1; u <= n; u++)
            for(int v = 1; v <= n; v++)
                dis[u][v] = min(dis[u][v], dis[u][k] + dis[k][v]);
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(d, INF, sizeof(d));
    for(int i = 1; i <= m; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        dis[u][v] = w;
    }
    return 0;
}

4.Johnson 求带负权的全源最短路

如果是稀疏图，那么跑 Floyd 显然不如跑 $n$ 遍 dijkstra。但是带负权图没有办法跑 dijkstra。我们的目的就是将所有边都变成正权的。

朴素地将每条边都加上一个常数 $c$ 是不可行的。此时路径所经过的边的多少会直接影响边权和。例如，如果实际最短路经过 $10$ 条边，在加上常数 $c$ 后，最短路边权和加上了 $6c$，但是经过了 $6$ 条边的路径只加了 $6c$，它们之间的大小关系可能会发生改变，所以这样不行。

有没有办法在把边权变为正的时候，不改变起点 $s$ 和终点 $v$ 的各条路径边权和的大小关系呢？

方法：

在图外建立一个 $0$ 号结点，从该节点向所有结点各连一条边权为 $0$ 的边，跑 $1$ 遍 BellmanFord 求出 $0$ 结点到各个结点的最短路长短分别为 $h_1 \sim h_n$，使边 $(u,v)$ 的新边权 $\hat w_{(u,v)} = w_{(u,v)} + h_u - h_v$。
跑 $n$ 遍 Dijkstra，求出所有结点对 $<s,v>$ 间的最短路。

解释：

对于边权为正的解释：根据前面的三角形不等式性质，我们有 $\mathrm D(s,v) \leqslant \mathrm D(s,u) + w_{(u,v)}$，代入这里，我们有 $h_v \leqslant h_u + w_{(u,v)}$ 即 $\hat w_{(u,v)} = w_{(u,v)} + h_u - h_v \geqslant 0$。
对于特定 $s$ 结点与 $v$ 节点间对应边权和大小关系不变的解释：考虑 $s，v$ 间的一条路径 $s \rightarrow p_1 \rightarrow p_2 \rightarrow \cdots \rightarrow p_k \rightarrow v$，我们总有：

\[\begin{aligned}\hat w_{总} &= \hat w_{(s,p_1)} + \hat w_{(p_1,p_2)} + \cdots +\hat w_{(p_k,v)}\\ &= w_{(s,p_1)} + h_s - h_{p_1} + w_{(p_1,p_2)} + h_{p_1} - h_{p_2} + \cdots + w_{(p_k,v)} + h_{p_k} - h_v \\ &= w_总 + h_s - h_v\end{aligned} \]

我们发现，此时对于 $s \rightsquigarrow v$ 中所有路径，他们都有着相同项 $h_s - h_v$，故而他们的大小关系都相同，我们的目的达成力！

时间复杂度： 首先跑了 $1$ 遍 BellmanFord，耗时 $O(nm)$。又跑了 $n$ 遍 dijkstra，稀疏图我们采取堆优化，耗时 $O(nm \log n)$。合起来就是 $O(nm \log n)$。

代码：

#include<bits/stdc++.h>
#define MAXN 8010
#define INF 1000000000
#define ll long long // 不开 long long 见祖宗
using namespace std;
ll lk[12010], ltp;
struct nds{
    ll nxt, y, w;
}e[12010];
void add(ll x, ll y,ll w)
{
    e[++ltp] = {lk[x], y, w};
    lk[x] = ltp;
}
struct Node{
    ll d, p;
    bool operator <(const Node &x)const{
        return x.d < d;
    }
};
priority_queue<Node> q;
ll n, m, h[MAXN], dist[MAXN], vis[MAXN];
void Dijkstra(ll s)
{
    for(ll i = 1; i <= n; i++) dist[i] = INF; // 初始化 INF 最好用循环
    memset(vis, 0, sizeof(vis));
    dist[s] = 0;
    q.push((Node){0, s});
    while(!q.empty()){
        Node tmp = q.top();
        q.pop();
        if(vis[tmp.p]) continue;
        vis[tmp.p] = true;
        for (ll ed = lk[tmp.p]; ed; ed = e[ed].nxt){
            ll edy = e[ed].y, edw = e[ed].w;
            if(dist[tmp.p] + edw < dist[edy]){
                dist[edy] = dist[tmp.p] + edw;
                if(!vis[edy])
                    q.push((Node){dist[edy], edy});
            }
        }
    }
    return;
}
ll BellmanFord()
{
    for(ll i = 1; i <= n; i++) dist[i] = INF;
    bool flag;
    h[0] = 0;
    for(ll i = 1; i <= n; i++){
        flag = false;
        for(ll u = 1; u <= n; u++){
            if(h[u] == INF) continue;
            for(ll ed = lk[u]; ed; ed = e[ed].nxt){
                ll edy = e[ed].y, edw = e[ed].w;
                if(h[edy] > h[u] + edw){
                    flag = true;
                    h[edy] = h[u] + edw;
                }
            }
        }
    }
    if(flag == true) return -1;
    else return 1;
}
int main()
{
    scanf("%lld%lld", &n, &m);
    for (ll i = 1; i <= m;i++){
        ll x, y, w;
        scanf("%lld%lld%lld", &x, &y, &w);
        add(x, y, w);
    }
    for(ll i = 1; i <= n; i++) add(0, i, 0);
    if(BellmanFord() == -1){printf("-1"); return 0;}
    for(ll i = 1; i <= n; i++)
        for(ll ed = lk[i]; ed; ed = e[ed].nxt)
            e[ed].w = e[ed].w + h[i] - h[e[ed].y];
    for(ll i = 1; i <= n; i++){
        Dijkstra(i);
        for(ll j = 1; j <= n; j++)
            if(dist[j] != INF) 
                dist[j] = dist[j] + h[j] - h[i];
    }
    return 0;
}

posted @ 2024-02-05 09:15 anjack_511 阅读(135) 评论(0) 编辑收藏举报

刷新页面返回顶部

anjack_511

【学习笔记】最小生成树与最短路

最小生成树与最短路

I 概念

II 最小生成树

1. Kruskal （贪心加边）

2. Prim （贪心加点）

III 最短路

0.最短路的一些基础知识

1.Bellman-Ford 求带负权的单源最短路

2.Dijkstra 求带正权的单源最短路

3.Floyd 求带正权的全源最短路

4.Johnson 求带负权的全源最短路

公告