真正把kmp算法中的next数组含义和求法讲明白
首先kmp算法是什么我就不啰嗦了。
直接讲next数组。
next数组我是这样定义的：该位置前面字符串的最长相同的真前缀和真后缀长度。
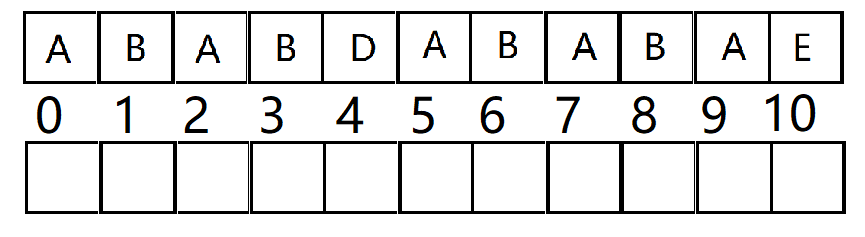
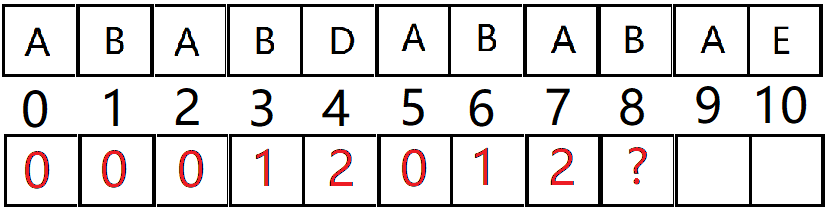
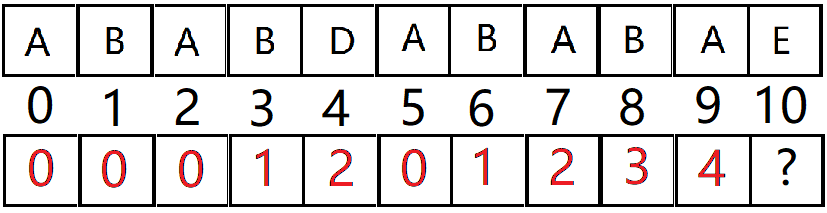
直接看这个字符串， ABABDABABAE：
中间一行是字符串的位置下标
首先，来看next数组第一个应该填什么。
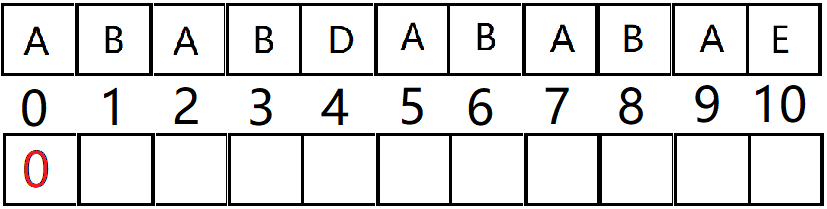
很明显，A这个位置前面压根没字符了，所以也不存在最长相同真前后缀。
按照定义，把next数组第一个填 0（实际一般填-1，这个是为什么后面再解释）。
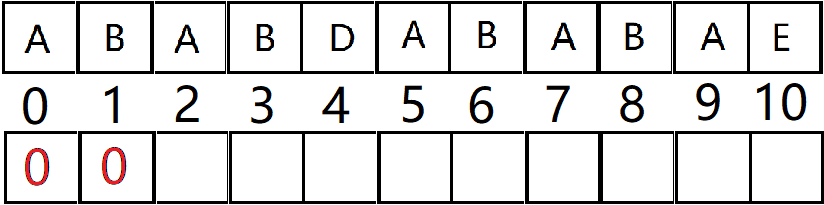
那么看第二个，字符是B，那么它前面是字符串A。
这里注意一下，求最长相同真前后缀，真前缀是不包括自身的，真后缀同理。
那么也很显然，A也没有真前后缀，更别说相同的真前后缀了。
所以next数组第二个也填0。
看第三个，字符是A，那么它前面是字符串AB。
这次有真前后缀了，真前缀只有一个A，真后缀只有一个B。
相同的真前后缀长度还是0。
看第四个，字符是B，那么它前面是字符串ABA。
ABA的 真前缀有A, AB。真后缀有A, BA。
好，这次不是0了，A和A相同。
因此最长的相同的真前后缀长度是1。
所以next数组第4个填1。
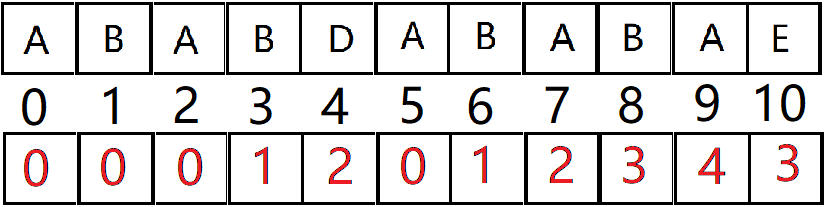
后面不用多说。按照这思路求出来的next数组应该是这个样子的：
这里我说个重要点：
next数组存的不是这个位置的 最长的相同的真前后缀长度，它存的是这个位置前面的字符串的 最长的相同的真前后缀长度。
所以看图中，最后E的位置，这时候字符串是ABABDABABAE其实根本没相同的真前后缀！
这个3指的是E前面的ABABDABABA最长的相同的真前后缀长度（即ABA）。
好，现在知道啥是next数组。但是这玩意怎么求呢？
我们是人，一眼看出相同前后缀。电脑不能看出来。
显然要设计一种算法，来求一个字符串的next数组。
有人说暴力跑一遍不就知道了？
别忘了，我们发明KMP算法就是简化字符串匹配的，你这里暴力匹配也谈不上 简化 二字了。
大家看数据结构书，看网上都会发现其实有一种简便方法让计算机快速求next数组。
这里先不贴代码。
先看一种情况：
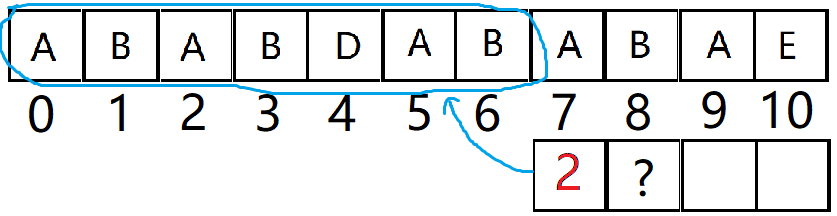
对于上面举的例子，怎么求 next[8] 呢？
把原数组称为array。
仔细想想就会发现，这个next数组其实是一个个按顺序求值的。
虽然不知道 next[8]（也就是字符B）对应的next数组值是多少，但是前面是已知的。
能不能根据前面已知的next数组值来推导？
注意到 next[7] = 2，这并不是指 array[7] 对应位置的字符串最长的相同的真前后缀长度。
前面已经说过这个 2 指的是 array[7] 对应位置前面字符的相同真前后缀，并不包括array[7]该位置本身。
实际上 arrary[7] 是A对 next[7] 有影响吗？ 根本没有。把 arrary[7] 换成 K 这个位置 next[7] 也是2，这是由前面决定的。
显然，这个字符 A 决定是后面 next[8] 的值，因为 next[8] 求得是 array[0]到array[7]这个字符串。
这也就是说：要知道 next[8] 的值只需要看 next[7] 和 arrary[7] 即可！
OK,我们再来看这个 2 ，它是指该位置前面的字符串 最长的相同的真前后缀长度 为2。
也就是ABABDAB 这个字符串，它们前面两个字符是AB,最后两个字符也是AB。
接下来我们知道，数组都是由0开始计数的。
那么其实 array[ next[7] ] = array[2] = 原数组的第三个。
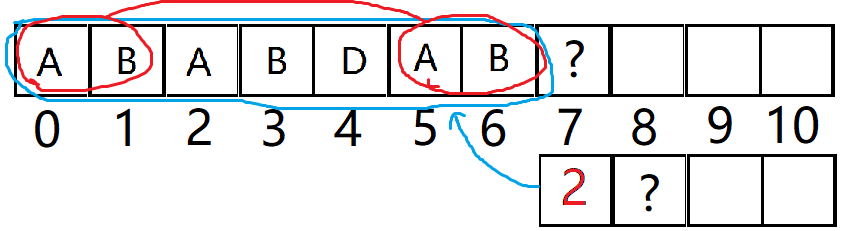
回到例子，
我们知道next[7]=2, 也就是array[7]前面两个( array[5] 和 array[6] )和字符串开头( array[0] 和 array[1] )两个相同。
显然，如果array[7] = array[2] = A,
那么 array[8]前面三个( array[5] array[6] array[7])和字符串开头( array[0] 和 array[1] array[2])三个相同。
得到结论一：
如果 array[ next[m] ] = = array[ m ]，那么next[ m+1 ] = next[ m ] + 1；
比如说 next[m]=K ，意味着m位置前面字符串前K个和后K个相同（这里的后K个，也就是m位置前K个）。
又由于数组从0计数，所以说 array[ next[m] ] = = array[ K ], 是指数组的第K+1个元素。也就是第一个不是前缀的位置!
现在m位置前字符串的前K个和后K个相同。而 array[ ] 数组的第K+1个元素 又等于 array[ m ]。
那么m+1个位置前字符串的前k+1个和后k+1个相同。
接下来讨论 array[ next[m] ] ！= array[ m ] 的情况。
还是这个例子，
next[10]应该是多少？
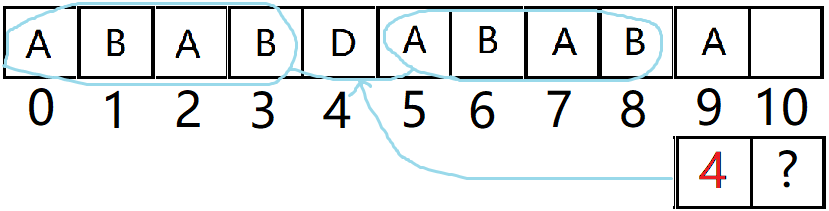
（array[ 9 ]=4，因为array[ 9 ] 前面字符串是ABABDABAB 相同部分是 ABAB 长度为4）
如图，
array[ next[9] ] = array[ 4 ] = D
而array[ 9 ] = A
array[ next[9] ] ！= array[ 9 ] ，
那么 next[ 10 ] 也不等于 next[ 9 ]+1了。
我们之所以能只比较两个位置的值等不等就能确定最长前后缀，是因为前面 已经求出来相同的地方了。
我们只要看 array[ 4 ] 和array[ 9 ]不同，是因为前面4个肯定相同，因为next[9]=4;
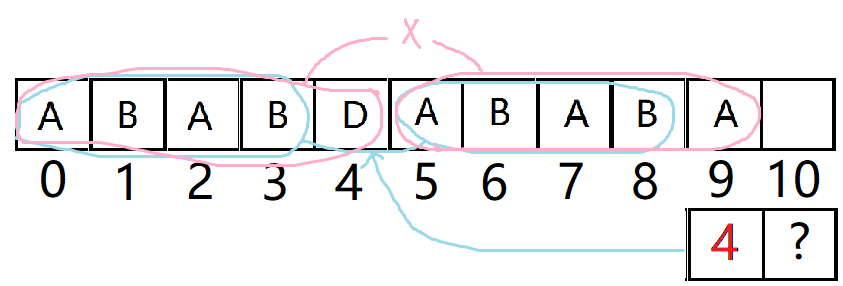
OK,取长度为5的前后缀不同，那么短一点的前后缀有可能会相同。
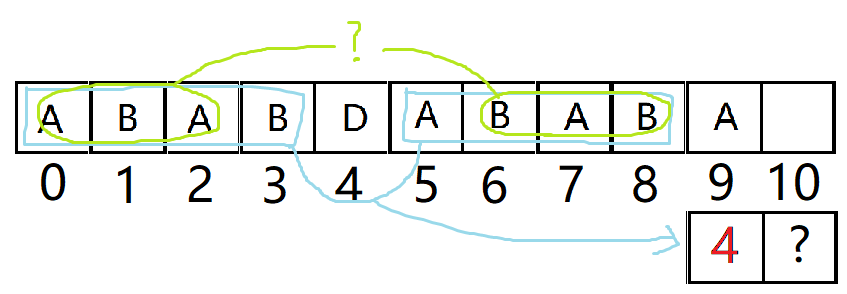
我们看看取4个的情况：
假如4长度的前后缀相同的话，就意味着array[0~3]=array[6~9]
也就意味着array[0~2]=array[6~8]
如图，只有绿圈里相同，我们才有必要比较 array[3] 是不是等于 array[9]。
问题是怎么知道绿圈里相不相同。
我们仔细想一下，蓝圈是已知 next[9]=4 而 相同的前后缀。
所以前后两个蓝色圈内字符串是完全相同的。
如果绿圈也相同，那不是代表绿圈是蓝色圈中字符串的相同前后缀？
而我们能不能知道蓝圈内的相同前后缀是什么？
当然可以：
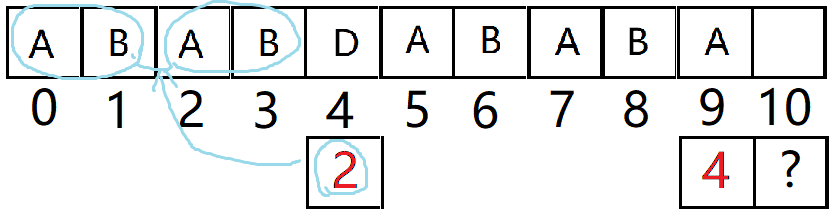
next[4]位置存储的就是前面4个的最长相同前后缀。
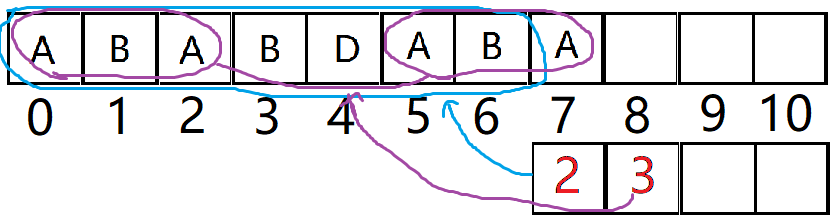
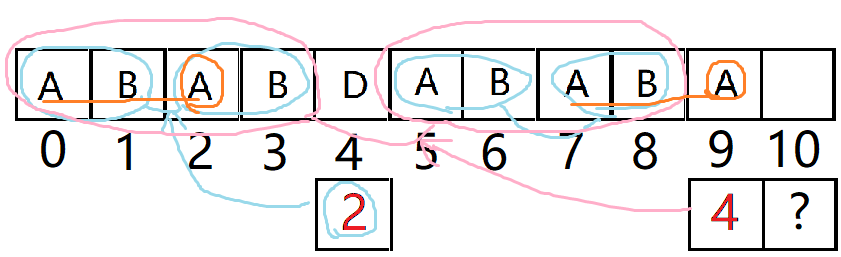
我们看next[9]=4。就是粉色圈子里的部分，两个字符串相同。
而next[4]=2。就是蓝色圈子里的部分，这四个部分都相同。
那么现在看橙色部分，就只要比较array[9] = array[2], 因为arr[0~1]和arr[7~8]肯定相同了，
比较发现确实array[9] = array[2]，那么得出结论：arrar[10]=3;
分析一下， next[9]=4,就是前9个字符中前4个和后4个相同。
那么，next[ next[9] ] =next [4]。
也就是第一个不属于前缀的位置，而next[4]代表是该位置前面字符串，就是之前的前缀。
next [4] = 2，也就是之前的前缀的相同前后缀的长度。
这也就是为什么上面第一种假设肯定不行了，因为next[ next[9] ] =next [4] = 2。
取 三个前缀后缀 肯定不等，等的话 next [4] 就等于3了。
因此 那一种情况中 array[9] 和 array[3] 都没有继续比较的必要了。
如果一直不等呢？
将arrat[9]改为E：
明显array[2]不等于array[9]；
那么就按照之前思路继续取：next[next[ next[9] ] ] = next[ next[ 4 ] ] = next [ 2 ] = 0。
比较 array[9] 和 array[0]，还是不等。
但是next[0]=0，继续嵌套不还是next [ 0 ]吗？
所以将next[0]=-1；
next[next[ next[9] ] ] = next[ next[ 4 ] ] = next [ 0 ] = -1；
OK，检测到-1就没必要继续嵌套了。
该位置不存在相同前后缀了。
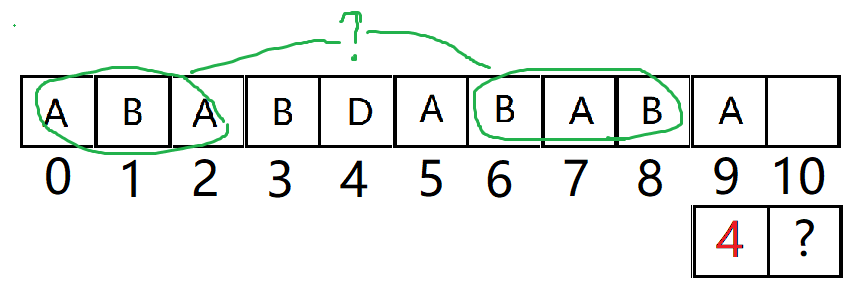
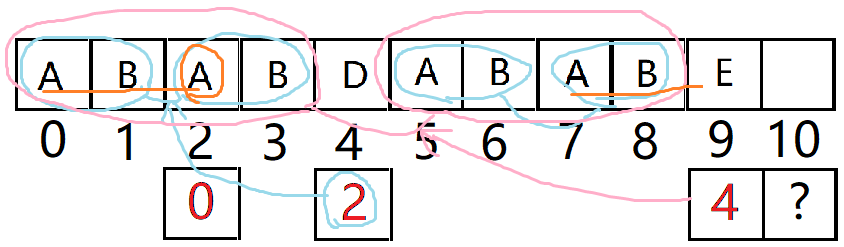
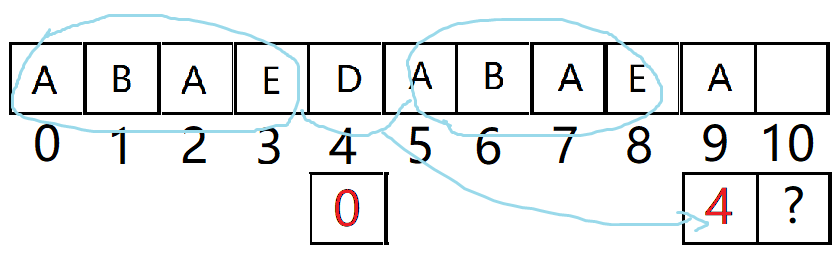
再举个例子
如图，将之前array[3] 和 arrar[8]改成E:
array[9] 等于 array[ next[9] ] 吗？（ array[ next[9] ] = array[4] ）
（等于的话next[10] = next[9] +1 =5）
不等于，比较 array[9] 和 array[ next[next[9] ] ] （array[ next[next[9] ] ] = array[ next[4] ] =array[0] ）
array[9] = array[0] = A 那么，next[10] = next[4] +1 =1
（不等于的话 next[next[next[9] ] ] = next[next[4] ] = next[0] = -1；next[10] =0）
结论二：
设置arrry[0]=-1;
如果 array[ next[m] ] ! = array[ m ]，
令t=m; t =next [t]
比较array[ next[t] ] 和 array[ m ]，相同的话 next[ m ]=next[ t ]+1；
不同的话 t =next [t] 继续比较。
当t=-1时，next[ m ]=0；
下面是随意找的一串代码：
1 void Getnext(int next[],String t) 2 { 3 int j=0,k=-1; 4 next[0]=-1; 5 while(j<t.length-1) 6 { 7 if(k == -1 || t[j] == t[k]) 8 //等于-1就不继续了，直接k++； next[j] = k=0了; 9 //不是-1还相同的话就直接k++；注意j先++了，所以是改变的下一个值。 10 { 11 j++;k++; 12 next[j] = k; 13 } 14 else k = next[k]; 15 } 16 }
以上
写的还是有点混乱，
图书windows自带画图软件画的，所以有些不整齐。
