树(数据结构二)
一、树
在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找,链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢,同样在链表中查找数据项效率就很低。综合以上情况,二叉树可以利用链表和有序数组的优势,同时可以合并有序数组和链表的优势,二叉树也是一种常用的数据结构。

1、基本术语有:
若一个结点有子树,那么该结点称为子树根的“双亲”,子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度:结点拥有的子树的数目
叶子结点:度为0的结点
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
树的高度:树中结点的最大层次
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
2、特点:
树具有的特点有:
(1)每个结点有零个或多个子结点
(2)没有父节点的结点称为根节点
(3)每一个非根结点有且只有一个父节点
(4)除了根结点外,每个子结点可以分为多个不相交的子树。
3、二叉树的性质
性质1:二叉树第i层上的结点数目最多为2i-1(i>=1)
性质2:深度为k的二叉树至多有2k-1个结点(k>=1)
性质3:包含n个结点的二叉树的高度至少为(log2n)+1
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:
n=n0+n1+n2
m=n1+2n2(一个叶子节点)
得出 n0=n2+1
普通二叉树的删除操作:
1.如果删除的是叶节点,可以直接删除;
2.如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置;
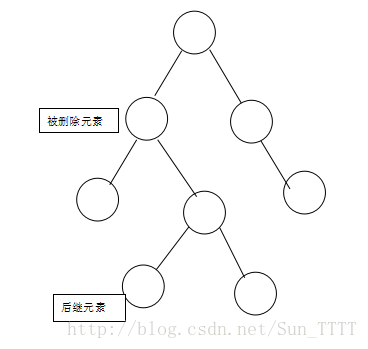
3.如果有两个子节点,这时候就可以把被删除元素的右支的最小节点(被删除元素右支的最左边的节点)和被删除元素互换,我们把被删除元素右支的最左边的节点称之为后继节点(后继元素),然后在根据情况1或者情况2进行操作。如图:
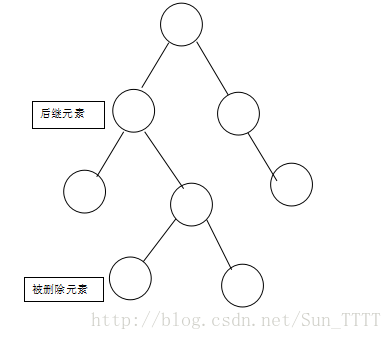
将被删除元素与其右支的最小元素互换,变成如下图所示:
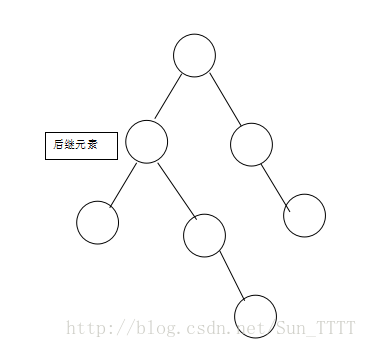
然后再将被删除元素删除:
完全二叉树
- 叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
平衡二叉树
- 左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
-
性质:
1. 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2. 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点(no duplicate nodes)。
二叉查找树(BST)
- 二叉查找树(Binary Search Tree),也称有序二叉树(ordered binary tree),排序二叉树(sorted binary tree)。
红黑树
- 性质:
1. 节点是红色或者是黑色;
2. 根节点是黑色;
3. 每个叶节点(NIL或空节点)是黑色;
4. 每个红色节点的两个子节点都是黑色的(也就是说不存在两个连续的红色节点);
5. 从任一节点到其没个叶节点的所有路径都包含相同数目的黑色节点;
B,B+,B*树
MySQL是基于B+树聚集索引组织表
https://blog.csdn.net/aqzwss/article/details/53074186
LSM 树
LSM(Log-Structured Merge-Trees)和 B+ 树相比,是牺牲了部分读的性能来换取写的性能(通过批量写入),实现读写之间的平衡。 Hbase、LevelDB、Tair(Long DB)、nessDB 采用 LSM 树的结构。LSM可以快速建立索引。