线性回归(二)--基础理论
基础理论
在(一)中,我们直接使用了sklearn中的线性回归函数,找到可能拟合的线性方程。在具体谈线性回归之前,我们先补充一点基础知识:
最小二乘法
首先,最小二乘法中的二乘实际上是非常有中国特色的叫法,二乘其实就是平方,因为在古代对于平方就是叫二乘的,和
y= x^2
非常形象,这点我们应该还是佩服老祖宗的智慧的。
所谓最小平方所涵义的最佳拟合,即残差(残差为:观测值与模型提供的拟合值之间的差距)平方总和的最小化。最小二乘法所得出的多项式,即以拟合曲线的函数来描述自变量与预计应变量的变异数关系。
举个例子:
某次实验得到了四个数据点 (x,y):(1,3)、(2,4)、(3,5)、(4,7)。我们希望找出一条和这四个点最匹配的直线,
y = a+bx_1
即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的a和b:
a+x_1 = 3
a+2x_1 = 4
a+3x_1 = 5
a+4x_1 =7
用数据公式表示:
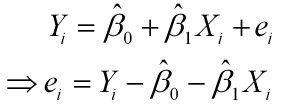
其中e为误差。
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值或者说是e最小,在数学上就称之为平方损失函数:
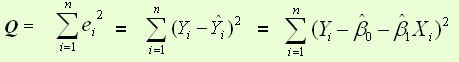 。根据数学知识,我们可以知道极值是偏导为0的点。也就是:
。根据数学知识,我们可以知道极值是偏导为0的点。也就是:
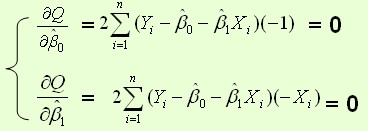
其结果为:
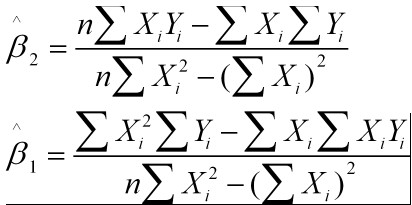
线性回归 Line Regression
线性回归主要是利用线性回归方程的最小二乘函数对一个或多个自变量和因变量之间的关系进行建模的一种回归分析。回归在数学上来说是给定一个点集,能够用一条曲线去拟合。如果这个曲线是一条直线就称之为线性回归,如果曲线是一条二次曲线就是二次回归。
线性回归模型最常用的数学模型如下:
θ在这儿称为权重。用向量的方式就是
所谓的回归就是我们拟合出来的值要尽可能的和真实值相比,误差值要比较小。这里就用损失函数或者称之为平方误差来表示这个值:

几何上的解释就是:图中线段距离(平方 欧式距离)的平均值,也就是需要最小化到分割面的距离和。
此时,回归问题就转化成了如何使得J(θ)最小的问题。
求解的方法最常用的有2个:
最小二乘法
最小二乘法的结果是:
所以对每一个样本点的值就是y=θX
梯度下降法
其结果是: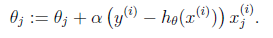
梯度下降法是按下面的流程进行的:
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
梯度方向由J(θ)对θ的偏导数确定,由于求的是极小值,因此梯度方向是偏导数的反方向



