Graph Contrastive Learning with Adaptive Augmentation 论文阅读笔记

Abstract

​ 尽管图CL方法得到了繁荣的发展，但图增强方案的设计——CL中的一个关键组成部分——仍然很少被探索。我们认为，数据增强方案应该保留图的内在结构和属性，这将迫使模型学习对不重要的节点和边缘的扰动不敏感的表示。然而，现有的方法大多采用统一的数据增强方案，如统一丢弃边和统一对特征进行重排，导致性能次优。在本文中，我们提出了一种新的具有自适应增强的图对比表示学习方法，该方法包含了图的拓扑和语义方面的各种先验。具体来说，在拓扑层面上，我们设计了基于节点中心性度量的增强方案来突出重要的连接结构。在节点属性级别上，我们通过向不重要的节点特征添加更多的噪声来破坏节点特征，以强制模型识别底层的语义信息。

Introduction

​ 我们认为，在上述方法中使用的增强方案存在两个缺点。首先，无论是结构域还是属性域的简单数据增强，如DGI中的特征转移，都不足以为节点生成不同的邻域（即上下文），特别是当节点特征稀疏时，导致难以优化对比目标。其次，以往的工作忽略了在进行数据扩充时节点和边影响的差异。例如，如果我们通过均匀地删除边来构造图视图，去除一些有影响的边会降低嵌入质量。由于对比目标学习到的表示对数据增强方案引起的破坏往往是不变的，因此数据增强策略应该自适应输入图，以反映其内在模式。同样，以除边方案为例，当随机去除边时，我们可以给不重要边的大概率，给重要边的小概率。然后，该方案能够指导模型忽略在不重要的边缘上引入的噪声，从而学习输入图下的重要模式。

​ 为此，我们提出了一种新的无监督图表示学习的对比框架，称为具有自适应增强的图对比学习(Graph Contrastive learning with Adaptive augmentation)，用GCA来表示。在GCA中，我们首先通过对输入执行随机破坏来生成两个相关的图视图。然后，我们使用对比损失来训练模型，以最大化这两个视图中节点嵌入之间的一致性。具体地说，我们提出了一种在拓扑和节点属性级别上的联合自适应数据增强方案，即去除边和掩蔽特征，为不同视图中的节点提供不同的上下文，从而促进对比目标的优化。此外，我们通过中心性度量来识别重要的边和特征维度。然后，在拓扑层次上，我们通过给不重要的边自适应的去除概率，以突出重要的连接结构。在节点属性级别上，我们通过向不重要的特征维度添加更多的噪声来破坏属性，以强制模型识别底层的语义信息。

​ 本文的贡献如下：

​ 我们提出了一个通用的对比框架，无监督图表示学习与强，自适应的数据增强。所提出的GCA框架在拓扑结构和属性层面上共同执行数据增强来适应图的结构和属性，这鼓励了模型从这两个方面学习重要的特征。

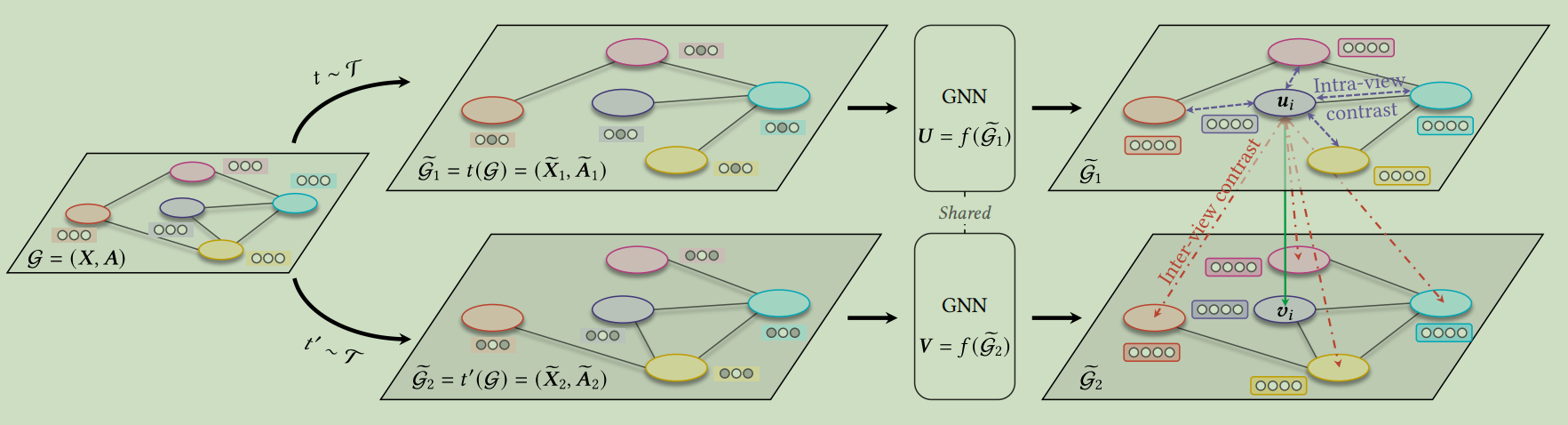
模型的结构图如下：

Method

​ 我们将详细介绍GCA，从整体的对比学习框架开始，然后是所提出的自适应图增强方案。最后，我们为我们的方法提供了理论证明。

​ 我们的目标是学习一个GNN编码器\(f(X,A)\)接收图的特征和结构作为输入，它产生低维的节点嵌入，

对比学习框架

​ 所提出的GCA框架遵循公共图CL范式，其中模型寻求最大限度地提高不同视图之间的表示一致性。具体地说，我们首先通过对输入执行随机图增强来生成两个图视图。然后，我们采用一个对比的目标，强制每个节点在两个不同视图中的编码嵌入彼此一致，并可以与其他节点的嵌入区分开来。

​ 我们采用了一个对比目标，即一个鉴别器，它将这两个不同视图中的同一节点的嵌入与其他节点的嵌入区分开来。对于任何节点vi，在一个视图中生成的嵌入ui被视为锚点，在另一个视图vi中生成的嵌入形成正样本，而在两个视图中生成的其他嵌入自然被视为负样本。在我们的多视图图CL设置中镜像InfoNCE目标，我们将每个正对（ui ，vi）的成对目标定义为

\[\begin{aligned}\ell(\boldsymbol{u}_i,\boldsymbol{v}_i)&=\\&\log\frac{e^{\theta(\boldsymbol{u}_i,\boldsymbol{v}_i)/\tau}}{e^{\theta(\boldsymbol{u}_i,\boldsymbol{v}_i)/\tau}+\sum_{k\neq i}e^{\theta(\boldsymbol{u}_i,\boldsymbol{\upsilon}_k)/\tau}+\sum_{k\neq i}e^{\theta(\boldsymbol{u}_i,\boldsymbol{u}_k)/\tau}},\end{aligned} \]

​ 定义了评价函数\(\theta(u,v)=s(g(u),g(v))\)，其中s为余弦相似度，g是一个非线性投影，以增强评价函数的表达能力。该方法中的投影函数g采用两层感知器模型实现。

​ 给定一个正对，我们自然地将负样本定义为两个视图中的所有其他节点。因此，负样本来自两个来源，即视图间节点和视图内节点，分别对应于等式中分母中的第二项和第三项由于两个视图是对称的，因此另一个视图的损失同样被定义为ℓ（vi，ui）。最大化的总体目标定义为所有正对的平均值，形式为

\(\mathcal{J}=\frac{1}{2N}\sum_{i=1}^{N}\left[\ell(\boldsymbol{u}_{i},\boldsymbol{\upsilon}_{i})+\ell(\boldsymbol{\upsilon}_{i},\boldsymbol{u}_{i})\right].\)

我觉得视图内对比有提升空间，相邻的可能比较相似，我们在对比的时候排除一些相似的节点

整体的算法流程如下：

自适应图增强

​ 本质上，最大化视图之间一致性的CL方法寻求学习对增强方案引入的扰动不变的表示。在GCA模型中，我们建议设计增强方案，以倾向于保持重要的结构和属性不变，同时干扰可能不重要的链接和特征。具体来说，我们通过随机去除图中的边和屏蔽节点特征来破坏输入图，对于不重要的边或特征，即不重要的边或特征较高，重要的边或特征较低。从平摊的角度来看，我们强调重要的结构和属性，而不是随机损坏的视图，这将指导模型保持基本的拓扑和语义图模式。

​

拓扑级别的增强

​ 我们考虑一种破坏输入图的直接方法，其中我们随机删除图中的边。在形式上，我们以概率从原始的边集中抽取一个修改后的子集\(\tilde{\mathcal{E}}\)

​ \(P\{(u,\upsilon)\in\widetilde{\mathcal{E}}\}=1-p_{u\upsilon}^{e}\)

​ \(p_{uv}^e\)是丢弃边(u,v)的概率，反映了边（u，v）的重要性，这样增强函数更有可能破坏不重要的边，同时在增强视图中保持重要的连接结构的完整

​ 在网络科学中，节点中心性是一种广泛使用的度量方法，它量化了图中节点的影响。我们基于两个连接节点的中心性定义了边(u,v)的边缘的中心性\(w_{uv}^e\)来衡量它的影响，给定一个节点的中心度量\(\varphi_{c}(\cdot)\)，我们将边的中心性定义为两个相邻节点的中心性得分，即\(w_{uv}^e=(\varphi_c(u)+\varphi_c(\upsilon))/2\)，在有向图中，我们简单的使用被指向节点的中心性，即\(w_{u\upsilon}^{e}=\varphi_{c}(\upsilon)\)，因为边的重要性通常是由它们所指向的节点来描述的。

​ 接下来，我们根据每条边的中心性值来计算它的概率。由于节点中心性值，比如度中心性，可能在数量级上变化，我们首先设置一个\(s_{u\upsilon}^{e}=\log w_{u\upsilon}^{e}\)，以缓解具有高度密集连接的节点的影响。然后通过将值转换为概率得到概率，定义为

\[p_{\boldsymbol{u}\upsilon}^e=\min\left(\frac{s_{\max}^e-s_{\boldsymbol{u}\upsilon}^e}{s_{\max}^e-\mu_{s}^e}\cdot p_{\boldsymbol{e}},p_{\tau}\right) \]

​ 其中pe是一个控制超参数去除边的总体概率，而pτ < 1是一个截断概率，用于截断概率，因为极高的去除概率会导致过度损坏的图结构。

​ 对于节点中心性函数的选择，我们使用以下三个中心性度量，包括度中心性、特征向量中心性和PageRank中心性。

度中心性

​ 节点度本身可以是一个中心性度量。在有向网络上，我们使用入度，因为有向图中的一个节点的影响主要是由指向其的节点所赋予的。尽管节点度是最简单的中心性度量之一，但它是相当有效和具有启发性的。例如，在引文网络中，节点代表论文，边缘代表引文关系，程度最高的节点很可能对应于有影响力的论文。

特征向量中心性

​ 将一个节点的特征向量中心性计算为其与邻接矩阵的最大特征值对应的特征向量。度中心性假设所有邻居对节点的重要性贡献相同，而特征向量中心性也考虑了相邻节点的重要性。根据定义，每个节点的特征向量中心性与其相邻节点的中心性之和成正比，连接到多个相邻节点或连接到有影响的节点的节点将具有较高的特征向量中心性值。在有向图上，我们使用右特征向量来计算中心性，它对应于进入的边。请注意，由于只需要前导的特征向量，因此计算特征向量中心性的计算负担可以忽略不计

PageRank中心性

​ PageRank中心性定义为由PageRank算法计算的排名权重。该算法沿有向边传播影响，将受影响量最大的节点视为重要节点。在形式上，中心性值被定义为

​ \(\sigma=\alpha AD^{-1}\sigma+1,\)

​ 对于无向图，我们对转换后的有向图执行PageRank，其中每条无向边都被转换为两条有向边。

节点属性级增强

​ 在节点属性级别上，我们通过随机屏蔽节点特征中为零的部分维数，将噪声添加到节点属性中。我们通过随机屏蔽节点特征中为零的部分维数，将噪声添加到节点属性中。形式为：

​ \(\widetilde{m}_i\sim\mathrm{Bern}(1-p_i^f)\)

​ $\widetilde{X}=[x_1\circ\widetilde{m};x_2\circ\widetilde{m};\cdots;x_N\circ\widetilde{m}]^\top $

​ 与拓扑级增强类似，概率\(p_i^{f}\)应该反映了节点特征的第i个维数的重要性。我们假设经常出现在有影响的节点中的特征维度应该是重要的，并定义特征维度的权重如下。对于稀疏的独热节点特征，即xui∈{0,1}，对于任何节点u和特征维度i，我们计算维度i的权重为

​ \(w_i^f=\sum_{u\in\mathcal{V}}x_{ui}\cdot\varphi_c(u)\)

​ 其中\(\phi_c(\cdot)\)是一个用于量化系欸但重要性的节点中心性度量，为了提供上述定义背后的一些直觉，考虑一个引文网络，其中每个特征维度都对应于一个关键字。那么，经常出现在一篇非常有影响力的论文中的关键词应该被认为是信息丰富和重要的

​ 与拓扑增强类似，我们对权值进行归一化，以获得表示特征重要性的概率。形式上：

​ \(p_i^f=\min\left(\frac{s_\mathrm{max}^f-s_i^f}{s_\mathrm{max}^f-\mu_s^f}\cdot p_f,p_\tau\right)\)

​ 在本文中，我们提出并评估了三个模型变量，分别表示为GCA-DE、GCA-EV和GCA-PR。这三个变量分别采用度、特征向量和页面秩中心性度量。请注意，所有的中心性和权重度量都只依赖于原始图的拓扑结构和节点属性。因此，它们只需要计算一次，并且不会带来太多的计算负担。

感觉跟上一篇根据相似度去噪的差不多，这里是利用了中心度来判断这个边适不适合去除