Variational Autoencoders for Collaborative Filtering论文阅读笔记
摘要
将VAE扩展到具有隐式反馈的协同过滤，这样能够超越线性因子模型。提出了一个具有多项式条件似然的神经生成模型。目前推荐系统用的比较多的是rank指标，这里本文也说明了为什么多项似然非常适合隐式反馈数据建模。相对于高斯函数和逻辑函数更加接近rank损失
马上提出了一个比较有意思的观点，虽然推荐被认为是一个大数据的问题，这篇文章认为，它代表了一个独特的具有挑战性的小数据问题，因为大多数用户只与一小部分的项目有联系。我们的目标是对每个用户的偏好集体的做出推断。
又介绍VAE在图像建模和生成方面取得了比较好的成果，但是用于推荐系统的工作很少，但是想要应用到上面，两个调整是很重要的
- 首先，需要使用多项式似然法来进行数据分布
- 然后，重新调整和解释了标准VAE的目标
也就是说，这篇文章的重点就是提出了一个多项式似然的方法来讲VAE应用到推荐系统上，这个是这篇文章的亮点所在
方法
\(x_u=[x_u1,...x_uI]^T\)代表了用户点击数量的一次词袋模型向量
模型
然后介绍一下这个模型的流程
模型首先从一个标准高斯模型先验中采样一个k维潜在的表示\(z_u\)，
然后\(z_u\)通过一个非线性函数\(f_{\theta}(\cdot)\)进行转换，来产生一个物品集合上的概率分布\(\pi(z_u)\)
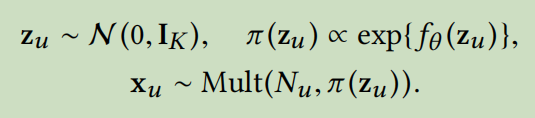
非线性函数f是参数为\(\theta\)的多层感知机，输出通过一个softmax函数来产生概率分布\(\pi(z_u)\)
\(N_u\)是点击率的总数，也就是\(N_u=\sum_ix_{ui}\)
观察到的词袋向量\(x_u\)是从一个概率分布为\(\pi(z_u)\)的多项式分布中抽样的
这里的点击只是一个泛指可以代表任何类型的互动，包括看，买和听。
用户在给定潜在表示下的多项式对数似然值为
\(logp_{\theta}(x_u|z_u)=\sum_i x_{ui}log\pi_i(z_u)\)
在VAE中，我们需要最大化期望而最小化KL散度
本文认为多项式分布非常适用于建模点击数据，这个似然函数鼓励将概率放在\(x_u\)的非0项上，但又因为模型限制了概率的总量，也就是\(\pi(z_u)=1\)所以项目必须竞争有限的预算，所以模型会将更多的概率分配给更有可能被点击的物品
后面介绍了一些高斯似然和逻辑似然
变分推断
为了学习生成模型，即估计函数f中的参数\(\theta\)，我们采用变分推断近似后验分布\(p(z_u|x_u)\)，这里用更简单的变分分布\(q(z_u)\)来近似这个后验分布
后面就是传统VAE的一些东西了，使得KL散度最小化
但是这个有一个缺点，那就是需要优化的参数的数量太多了，参数的个数随样本的数量而增加。所以，我们可以用一个\(x_u\)的函数来代替参数，难找的函数就用神经网络来替代，最终就是优化参数\(\{\mu_u,\sigma_u^2\}\)
使得KL散度最小化
以上是VAE算法的伪代码
然后后面采用了\(\beta\) VAE来代替传统的VAE
其中还有一张关于VAE分类的图
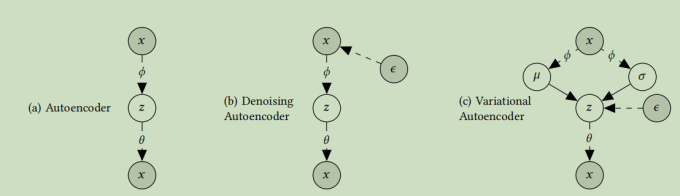
后面就是设计实验了，没有什么有新意的东西了
总结一下，本文就是开发了一种用于对隐式反馈数据的协同过滤的变体VAE，引入了由神经网络参数化的多项式似然函数的生成模型，表明了多项似然特别适合于建模用户隐式反馈数据，然后它的未来工作就是研究为什么引入正则化参数\(\beta\)效果会更好，然后试着在VAE中引入条件进行扩展，看能不能提高性能
