GNN学习 GNN增强和训练
GNN学习 GNN增强和训练
1.图增强
分为结构增强和特征增强
原始的图数据可能并不适合直接用于GNN
特征层面:
- 输入图可能缺少特征
结构层面:
- 图过于稀疏,导致信息传递效率低
- 图过于稠密,导致信息传递代价太高
- 图可能太大,导致GPU装不下
输入图很难是恰好适宜embedding的最优计算图
图增强方法
图特征增强
- 缺少图特征,就进行特征增强
图结构增强
- 图过于稀疏:增加虚拟节点或边
- 图过于稠密:在信息传递时抽样邻居
- 图太大:在计算embedding时抽样子图
图特征增强
存在的问题:
输入的图不含有节点的特征
解决方法
1.constant
我们可以给每个节点分配常数特征
2.onehot
给每个节点分配唯一的ID,将ID转换为独热编码向量的形式
为什么需要特征增强·
因为GNN很难学到特定图结构的问题
常见的节点特征有:
- 节点度数
- 聚集系数
- PageRank
- 中心性
图结构增强
1.添加虚拟节点或虚拟边
为了增强稀疏图
1.添加虚拟边
例子:在二部图的两跳就能达到节点添加虚拟边
一个好处就是在由作者-论文组成的二部图中,可以增加合作作者已经同作者论文之间的连接
2.添加虚拟节点
可以添加一个虚拟节点,这个虚拟节点与图上所有节点连接,这样会导致所有节点的最长距离变成2,这样稀疏图上的信息传递的速度就能大幅提升
2.对邻居节点采样
也就是在传递信息时,不使用一个节点的全部邻居,而改为抽样一部分邻居,缺点是可能会损失一些重要信息,不过我们可以每次抽样不同的邻居来增强模型的健壮性
2.GNN训练
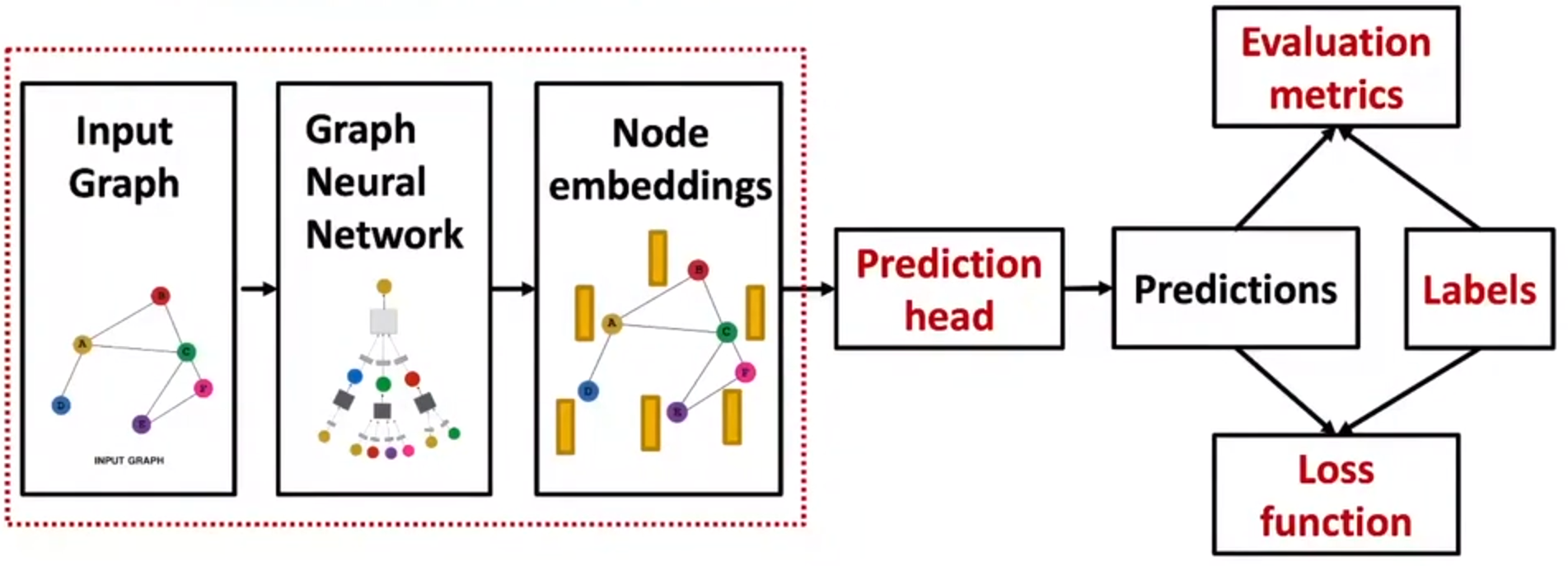
GNN训练的主要流程:
输入图->用GNN训练->得到节点的embedding->Prediction head->得到最终的预测
Prediction Head
prediction head有不同的粒度
- 节点级别
- 边级别
- 图级别
节点级别
可以直接用节点嵌入来进行预测
假设我们最后得到的节点嵌入是d维的,我们需要做k维的预测
- 分类:在k个类别里面做分类
- 回归:在k个目标里做回归
以及
边级别
也是用节点嵌入来进行预测
假设也是进行k路预测
那么这个Head该怎么选呢
1.采用连接层和线性层
Linear层可以将2d维的embedding映射到k维的embedding
2.采用点积
不过这个只适用于1路预测
如果想要做k路预测,我们可以对其进行扩展
图级别
假设进行k路预测
Head跟AGG很相似,可以是Mean,Max或者Sum
如果想要比较不同大小的图,Mean方法可能会比较好
如果关心图的大小等信息,Sum方法可能会比较好
但是在大图上采用Global Pooling方法会有信息丢失的问题
为了解决这个问题,我们采用分层(hierarchical)的global pooling
分层的聚合所有节点的embedding
预测结果和标签
ground-truth的来源
- 有监督问题的标签
- 无监督问题的信号
有监督学习:直接给出标签
无监督学习:使用图自身的信号
但是有时候这两种的分别比较模糊,无监督学习任务中也有你有有监督的任务,比如训练GNN预测节点的cluster coefficient
有监督学习
节点标签:比如论文属于哪一个学科
边标签:比如交易是否有欺诈行为
图标签:分子是药的概率
建议无监督学习任务归类到这三种粒度下的标签预测任务,比如聚类可以看作节点粒度上的节点属于哪一类的预测任务
无监督学习
没有外部标签时,用图自身的信号来作为有监督学习的标签
节点级别:计算节点的一些统计量,cluster coefficient,PageRank等
边级别:预测两个节点之间是否有边
图级别:计算图统计量,比如预测两个图是否同构
一些评价指标:
Accuracy:
Precision:
Recall:
F1-score:
也就是P和R的调和平均数
ROC Curve
就是TPR和FPR之间的权衡
TPR=Recall
FPR=
AUC就是ROC曲线下的面积
AUC越大越好,AUC=0.5说明是随机分类器,1是完美分类器
训练的一些细节
测试集的划分方式需要注意
图神经网络数据集比较特殊,因为每一个数据点是一个节点,数据点不是独立的
解决方法:
1. Transductive setting
输入的图在所有划分中都可见,只是切分节点的标签
也就是在计算embedding时使用整个图,在训练的时候使用节点1,2的标签
2. inductive setting
去掉划分的数据集之间的连接,得到许多互相无关的图,这样不同划分之间的节点就不会互相影响
区别和联系
transductive setting
- 测试集,训练集和验证集都在同一张图上
- 全图在所有划分中可见
- 适用于节点和边预测任务
inductive setting
- 测试集,训练集和验证集都在不同的图上,整个数据集由多个图构成
- 每个划分只能看到划分内的图,最后的模
- 型可以泛化到没见过的图上
- 适用于节点,边和图预测任务
三种不同任务
1.节点分类任务
一个看到全图结构,一个需要切分图
2.图预测任务
只适用于inductive setting,将不同的图划分到不同的split中
3.连接预测任务
是一个无监督任务,需要自行建立标签,自主切分数据集
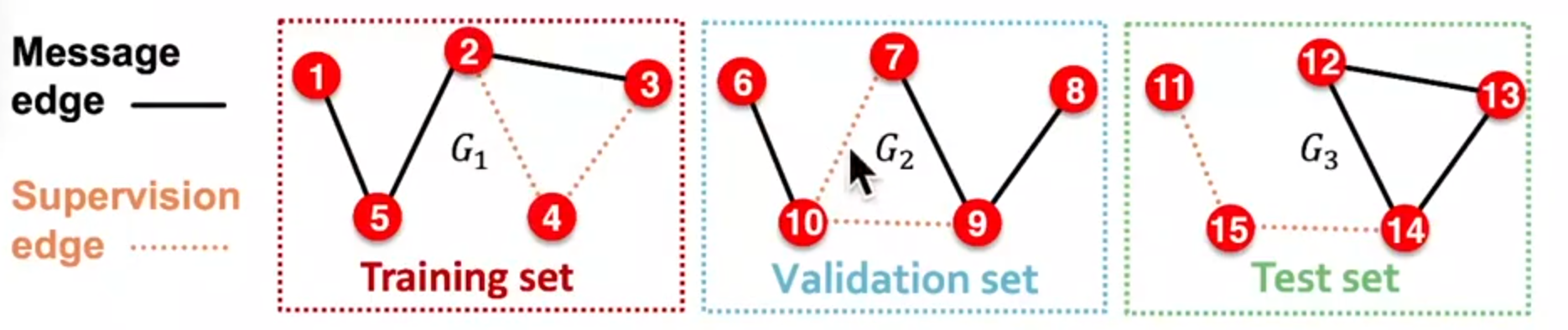
切分数据集时需要切两次
第一步需要将边分为信息传递边(message edges)和要预测的边(supervision edges),将数据给GNN时只留下信息传递边
第二步才切分数据集
选择一:Inductive link prediction split
每种图都有两种边,message edges和supervision edges
选择二:transductive link prediction split
在一张图上进行切分
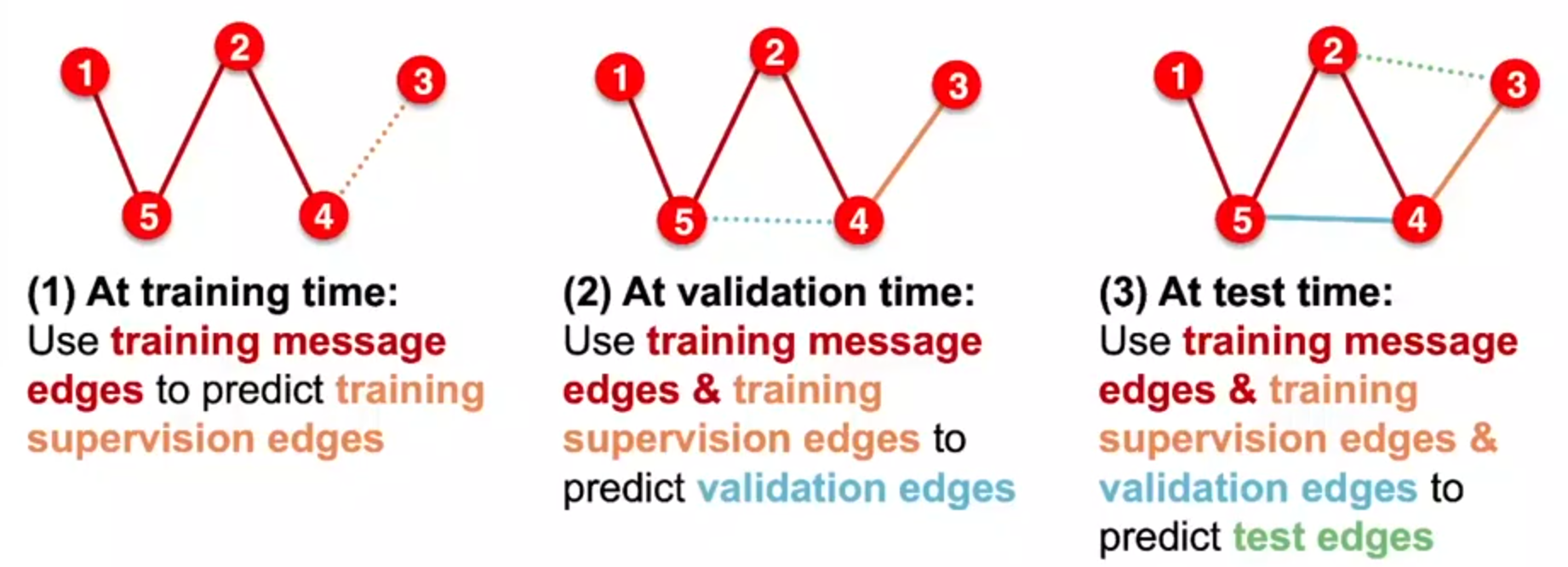
在训练时留出验证集和测试集的边
在训练时也要留出supervision edges
在训练时,用training message edges来预测training supervision edges
在验证时,用training message edges和training supervision edges来预测validation edges
在测试时,用training message edges,training supervision edges和validation edges来预测test edges
总的来说,这个划分是划分出了四种边
- training message edges
- training supervision edges
- validation edges
- test edges


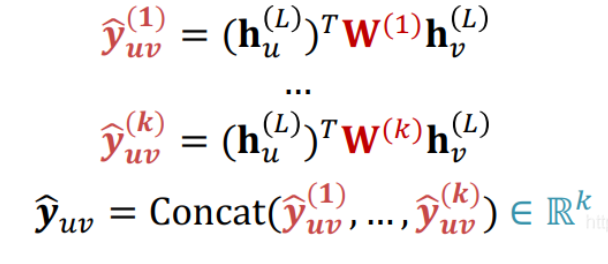


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律