GNN学习 GNN Layer
GNN学习 GNN Layer
GNN的通用框架
- 1.对GNN的一个网络层进行信息转换和信息聚合两个操作
- 2.连接GNN的网络层
- 3.图增强,分为图特征增强和图结构增强
- 4.学习目标,有监督学习还是无监督学习,节点/边/图级别
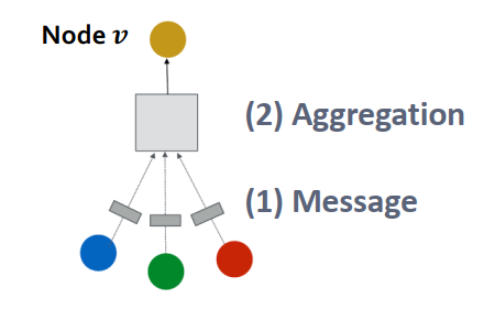
1.信息转换和信息聚合
GNN Layer=Message+Aggregation
不同的实例有不同的信息转换和增强的方法
GNN单层网络的目标是将一系列向量压缩到一个向量中
Message computation
\(m_u^l=MSG^l(h^{l-1}_u)\)
每个节点都会产生信息,这些信息将会被传递到其它节点
MSG可以是一个矩阵W
Message Aggregation
\(h_v^l=AGG^l({m_u^l,u\in N(v)})\)
每个节点都要聚合从其它的邻居节点处获得的信息
AGG可以是Sum,Mean或者Max
存在的问题:
会导致节点自身的信息丢失,因为在计算时不会包含节点本身,解决方法就是在计算\(h_v^l\)时包含\(h_v^{l-1}\)
- 在信息传递时,对节点本身和邻居应用不同的权重矩阵
- 在信息聚合时,将邻居节点与自身信息进行聚合
\(m_u^l=W^lh^{l-1}_u\)
\(m_v^l=B^lh^{l-1}_v\)
\(h_v^l=CONCAT(AGG({m_u^l,u\in N(v)}),m_v^l)\)
所以一个单层的神经网络就是将这些东西结合在一起
- Message:\(m_u^l=MSG^l(h^{l-1}_u),u\in {N(v)\cup v}\)
- Aggregation:\(h_v^l=AGG^l(\{m_u^l,u\in N(v)\}),m_v^l)\)
在做完前面的步骤之后,我们可以将其经过一个非线性激活函数\(\sigma\),例如ReLU或者Sigmoid
经典案例分析
1.GCN
前面讲到的GCN的传递函数
\(h_v^l=\sigma(\sum_{u\in N(v)}W^l\frac{h_u^{l-1}}{\left | N(v) \right | })\)
累加号就是聚合的过程
累加号后面的就是信息传递的过程
详细来说:
Message:
\(m_u^l=\frac{1}{|N(v)|}W^lh^{l-1}_u\)
Aggregation:
\(h^l_v=\sigma(Sum(\{m_u^l,u\in N(v)\}))\)
2.GraphSAGE
这个方法包含了节点本身的一些信息
\(h_v^l=\sigma(W^l\cdot CONCAT(h_v^{l-1},AGG(\{h_u^{l-1},\forall u\in N(v)\})))\)
Message过程在AGG里进行计算了
先聚合邻居节点,再聚合自身节点
AGG可以是Sum,Mean甚至是LSTM
之后要进行归一化,我们这里采用L2 Normalization
对每层都进行L2归一化,也就是
\(h_v^l\leftarrow \frac{h_v^l}{||h_v^l||} \forall v\in V\)
并且\(||u||_2=\sqrt{\sum_iu_i^2}\)所以被称为L2-norm
3.GAT(Graph Attention Network)
层之间的传递公式为
\(h_v^l=\sigma(\sum_{u\in N(v)}\alpha_{vu} W^lh_u^{l-1})\)
其中\(\alpha_{vu}\)被称为注意权重(attention weight)
例如GCN里\(\alpha_{vu}=\frac{1}{|N(v)|}\)
GAT
如何学习\(\alpha_{vu}\)
目标:确定图中每个节点的不同邻居的重要性
想法:
- 节点关注邻居的信息
- 间接的确定邻居不同节点的不同的权重
注意力机制
\(\alpha_{vu}\)是作为注意力机制a的副产品被计算的
首先计算两个节点之间传递信息的注意力系数\(e_{vu}\)
\(e_{vu}=a(W^lh_u^{l-1},W^lh_v^{l-1})\)
注意力系数表示了从节点u传递给节点v的信息的重要性
之后我们对注意力系数归一化,得到注意力权重,这里可以采用softmax来进行归一化
那么注意力机制的形式是什么
我们可以用简单的单层神经网络来作为注意力机制a
那么相当于
\(e_{vu}=Linear(W^lh_u^{l-1},W^lh_v^{l-1})\)
也可以引入多头注意力机制
最后对输出进行聚合
\(h_v^l=AGG(h_v^l[1],h_v^l[2],h_v^l[3])\)
注意力机制的主要好处就是确定不同邻居节点的不同重要性
A对B的注意力和B对A的注意力可以不同
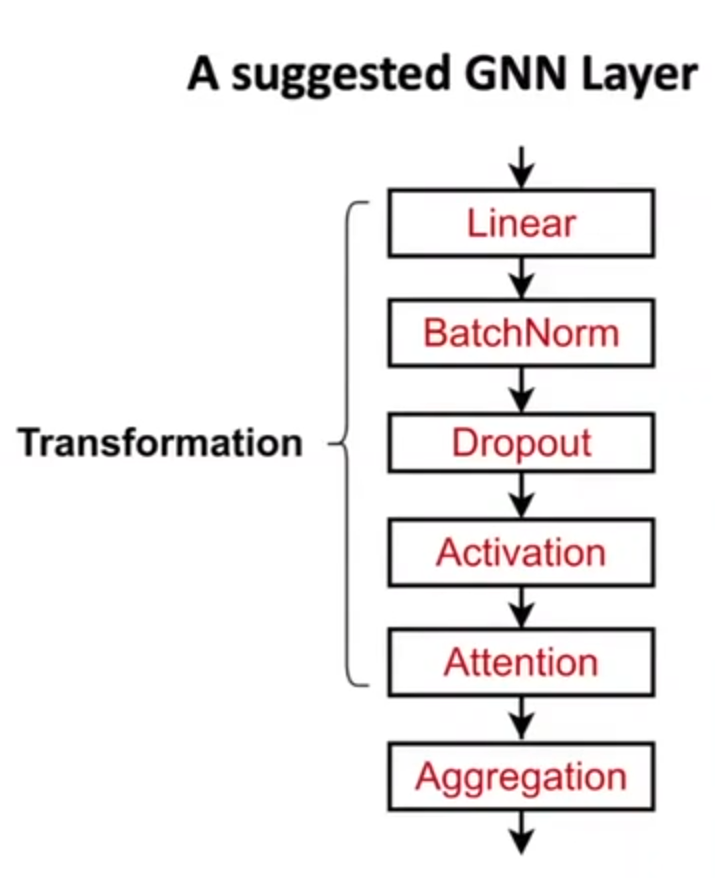
实际的GNN Layer搭建如下
2.GNN Layer的连接
一个经典的想法是顺序的堆叠GNN Layer
但是顺序堆叠会导致过平滑问题(over-smoothing problem):也就是不同节点的嵌入向量会收敛到同一个值
对K层的GNN来说,每个节点的感受野(Receptive field)是它K跳的邻居,K越大,节点的感受野就越大
对两个节点来说,K变大,感受野重合部分就会迅速变大
解决过平滑问题的方法:就是要谨慎的考虑增加GNN的层数
- 分析解决问题所需的必要感受野
- 设置GNN层数略大于我们想要的感受野
GNN层数较少
那么既然GNN Layer的层数有限,我们应该如何增加GNN的表现力
解决方法1:增加单层GNN Layer的表现力:
将信息转换的过程或者信息聚合的过程由简单的线性网络变成深度的神经网络
解决方法2:添加不是用来传递信息的网络层
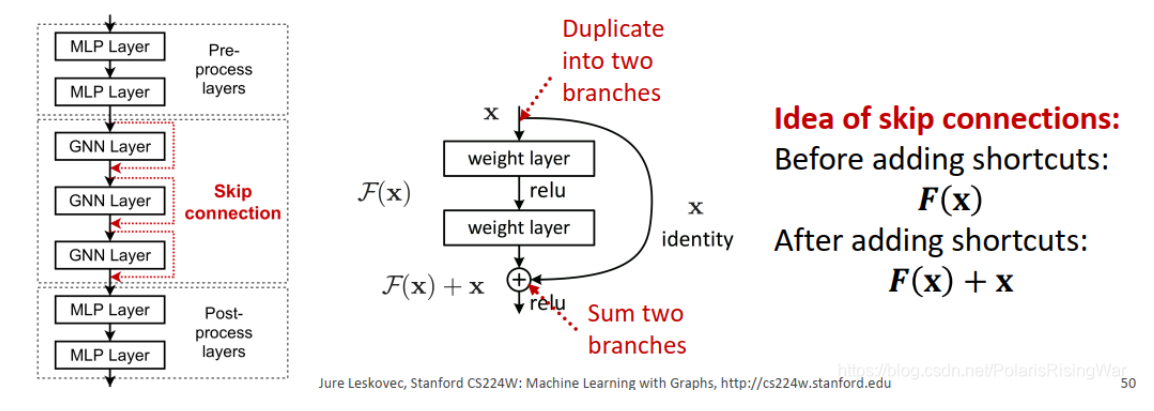
可以在GNN Layer之前与GNN Layer之后添加MLP层,分别叫pre-process layers和post-process layers
- pre-process layers在节点特征需要进行编码时就比较重要,比如节点表示文字或者图片
- post-process layers在节点embedding的基础上进行推理和转换就比较重要,比如图分类和知识图谱
GNN层数较多
如果实际任务需要多层GNN网络,我们可以在GNN模型中添加skip commections
我们可以注意到,靠前的GNN层能够更好的区分节点,所以我们可以在最终的embedding上增加靠前GNN层的影响力,通过像GNN中添加shortcut
为什么skip connection会有效
因为相当于创造了多个模型,N个skip connection相当于创建了\(2^N\)条路径,相当于获得了一个浅的GNN和深的GNN的融合模型
应用skip connection
传统的GCN Layer:
\(h_v^l=\sigma(\sum_{u\in N(v)}W^l\frac{h_u^{l-1}}{\left | N(v) \right | })\)
添加了skip connection的GCN layer
\(h_v^l=\sigma(\sum_{u\in N(v)}W^l\frac{h_u^{l-1}}{\left | N(v) \right | }+h_v^{l-1})\)
skip connection可以跨越多层,也可以直接跨到最后一层,在最后一层聚合之前各层的embedding

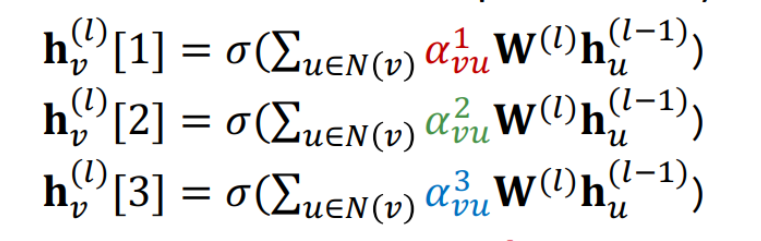

 浙公网安备 33010602011771号
浙公网安备 33010602011771号