GNN学习 Node Classification
GNN学习 Node Classification
任务:已知图中一部分节点的标签,如何将分配标签到其它节点上
Node Classification
给一部分节点的标签,预测没有标签的节点的标签,这是一个半监督节点分类任务
message passing
相似的节点中存在链接
集体分类(collective classification):一起给网络中的所有节点分配标签
有三种实现技术
- Relational classification
- Iterative classification
- Belief classification
Correlations Exists in Networks
相似的行为在网络中会互相关联
Correlation:相近的节点有相同的分类
导致关联性的主要以来类型
- 同质性(homophily):个体特征影响社交连接
- 影响(influence)社交连接影响个体特征
Homophily
相似节点会倾向于交流和关联
例子:同领域的研究者更容易建立联系
Influence
社交链接会影响个人行为
例子:用户将喜欢的音乐推荐给朋友
Classification with Network Data
相似的节点会在网络中更加靠近,或者直接相连
Guilt-by-association:如果我与具有X的标签相连,那么我很可能也具有标签X
预测节点v的标签要
- v的特征
- v邻居的标签
- v邻居的特征
Collective Classification
是一个概率框架
根据马尔科夫假设:节点v的标签\(Y_v\)取决于其邻居\(N_v\)的标签,也就是\(P(Y_v)=P(Y_v\mid N_v)\)
Collective Classification有三个步骤:
- 分配节点初始标签(Local Classifier)
- 捕获关系(Relational Classifier)
- 传播关系(Collective Inference)
Local Classifier
- 基于节点的属性预测标签
- 标准分类任务
- 不使用网络结构信息
Relational Classifier
- 基于邻居节点的标签和特征来预测节点标签
- 使用了网络结构信息
Collective Inference
- 在每个节点上迭代的应用relational classifier
- 迭代至邻居间标签不一致最小化
- 网络结构影响最终预测结果
Relational Classification and Iterative Classification
Relational classifiers
基本思想:节点v的类概率\(Y_v\)是其邻居类概率的加权平均值
对应有标签节点,就初始化为其真实标签
对于无标签节点。就初始化为0.5
以随机顺序更新所有无标签节点,直至收敛或达到最大迭代次数
对于每个节点v和标签c,我们采用公式
$P(Y_v=c)=\frac{1}{ {\textstyle \sum_{(v,u)\in E}}} {\textstyle \sum_{(v,u)\in E}}A_{v,u}P(Y_u=c) $
来对其进行更新
其中\(A_{v,u}\)是边v到u的权重
\(P(Y_v=c)\)表示节点v有标签c的概率
当然,对于最开始已经有标签的节点就不进行更新,只更新最开始没有标签,需要我们去预测的节点
当有节点连续两次迭代不发生变化,我们认为这个节点已经收敛了,之后我们就不再更新这个节点的值了
缺点:
- 可能不会收敛
- 无法利用节点的特征信息
Iterative classification
主要思想:基于节点特征\(f_v\)已经邻居节点的特征\(z_v\)来进行分类
方法:训练两个分类器
- \(\phi_1(f_v)\)基于节点的特征向量\(f_v\)来对标签进行预测
- \(\phi_2(f_v,z_v)\)基于节点的特征向量\(f_v\)和邻居节点的标签summary \(z_v\)来进行预测
Computing the Summary \(Z_v\)
\(Z_v\)是一个向量,它可以是
- 邻居标签的直方图
- 邻居标签中出现次数最多的标签
- 邻居标签的类数
Iterative classifier的结构
阶段1:基于节点特征建立分类器
- 在训练集上训练上面提到的两个分类器
阶段2:迭代至收敛
- 在测试集上,利用\(\phi_1\)先来预测标签,然后\(\phi_2\)利用前面预测的标签计算出\(Z_v\)并且预测最终的标签
- 对每个节点v重复下面的步骤
-
- 基于所有与v相连的节点的标签\(Y_u\)来计算\(z_v\)
- 基于\(\phi_2\)计算出的\(z_v\)来更新\(Y_v\)
- 迭代至收敛或达到最大迭代次数
- 最后模型不一定能够收敛
Loopy belief propogation
belief propogation是一种动态规划的方法,用于回答图中的概率问题
邻居节点之间迭代的传递信息
当达成共识时,计算最终的置信度
Loopy BP Algorithm
从i传递给j的信息取决于:
- i从邻居接受到的信息
- 每个邻居给i对其状态的置信度的信息
一些数学符号:
- Label-Label potential matrix \(\psi\) :表示节点和它邻居之间的依赖,如果j的邻居节点i属于类\(Y_i\),那么\(\psi(Y_i,Y_j)\)与j属于类\(Y_j\)的概率成比例
- Prior belif \(\phi\):\(\phi(Y_i)\)与节点i属于类\(Y_i\)的概率成比例
- \(m_{i\rightarrow j}(Y_j)\)是i对j属于类$Y_j $的信息或者说是估计
- $\mathcal{L} $是所有类或者说是标签的集合
具体算法如下:
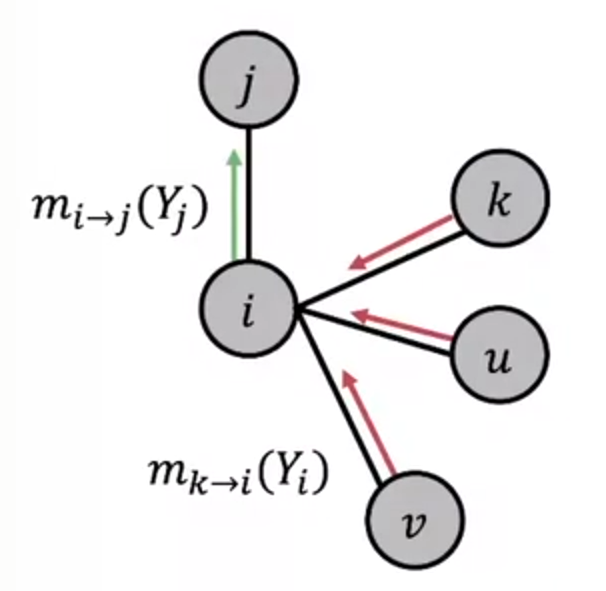
\(m_{i\rightarrow j}(Y_j)= {\textstyle \sum_{Y_i\in \mathcal{L}}\psi (Y_i,Y_j)\phi _i(Y_i)\prod_{k\in N_i\setminus j}m_{k\rightarrow i}(Y_i)}\)
示意图如下:
收敛后
\(b_i(Y_i)\)是节点i属于类\(Y_i\)的置信度
\(b_i(Y_i)=\phi _i(Y_i) {\textstyle \prod_{j\in N_i}m_{j\rightarrow i}(Y_i)}\)
不过以上都是无环的情况
当存在有环的情况时,不同子图传递的信息直接就不再独立了
并且因为有环,会存在信息增强的问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号