GNN学习 PageRank
GNN学习 PageRank
Graph as Matrix
将图表示为矩阵有三个好处
- 通过Random walk确定node的重要性
- 通过矩阵因式分解(MF)获得node embedding
- 将其他的node embedding表示为MF
Web as Graph
可以将web看作一个图
- node就是web page
- edge就是超链接
但是并不是所有的页面都是有效的,所以我们要给网页分级
我们可以用链接分析方法来计算图中node的重要性
- PageRank
- Personalized PageRank (PPR)
- Random Walk with Restarts
Links as votes
如果一个页面有越多的链接,那么这个页面就越重要
但是链接分为进入链接(in-link)和外出链接(out-link),一般我们认为in-link更具有代表性
但是不是所有in-link的重要性都是相同的
PageRank: Flow Model
如果一个page i 的重要性为 ri ,有di 个out-link,那么每个out-link的vote为ri /di
page j 的重要性dj 为所有in-link的vote之和
那么对一个图来说,我们就可以根据上面的算法列出许多等式,接下来该如何求解
Matrix Formulation
Stochastic adjacency matrix
如果j有dj 个out-link,那么对于所有的i,如果j->i 那么Mij =1/dj
M就是列随机矩阵,列的和为1
Rank vector r
记录每个页面重要性的向量,所有页面的重要性之和为1
那么flow equation为:
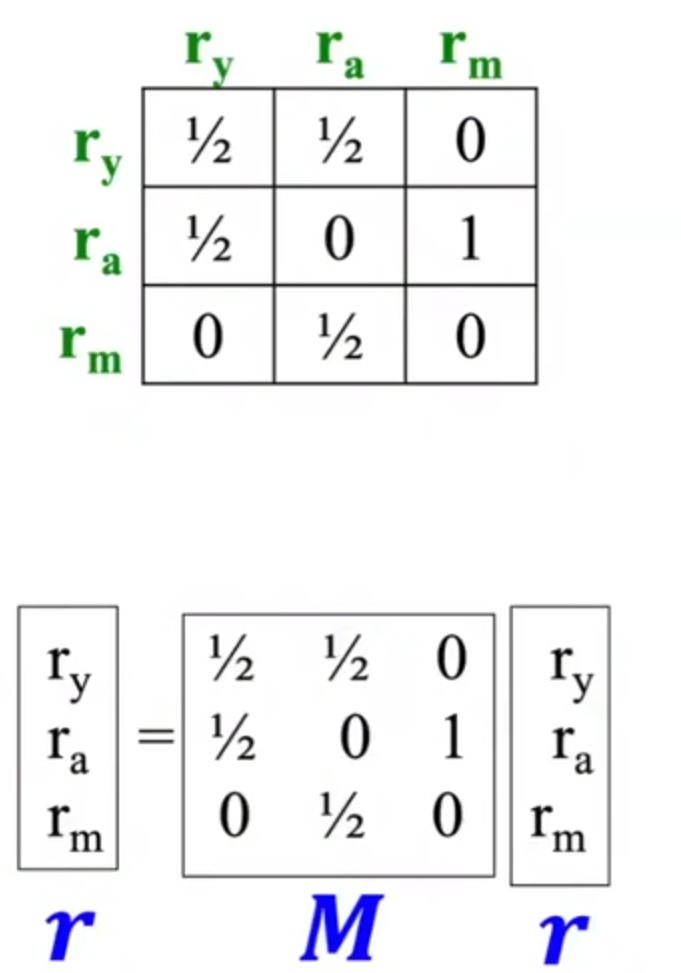
r=M \(\cdot\) r
例子:

Connection to Random Walk
假设一个网上冲浪的随机游走,在时间t处于page i上,在时间t+1时随机从out-link中选一条进行游走
向量p(t)的第i个坐标是t时间在网页i的概率,所以向量p(t)是网页间的概率分布向量
The Stationary Distribution
p(t+1)=M\(\cdot\)p(t)
当p(t+1)=M\(\cdot\)p(t)=p(t)时,我们就认为随机游走到达了一个稳定的状态,p(t)就是随机游走的稳态分布
所以我们原来的排名向量r要达到稳态分布则需满足r=M\(\cdot\)r
最后,flow equation为
1\(\cdot\)r=M\(\cdot\)r
那么r就是M的特征值为1所对应的特征向量
所以主特征向量r即为PageRank
Solve PageRank
迭代步骤
根据\(r_{j}^{t+1}=\sum_{i\longrightarrow j}^{}\frac{r_{i}^{t} }{d_{i}}\)
计算每一个节点的page rank
直到
\({\textstyle \sum_{}^{}\left | r_{i}^{t+1} -r_{i}^{t} \right | } <\epsilon\)
Power Iteration Method
初始化\(r^{0}=[1/N,...,1/N]^{T}\)
迭代:\(r^{t+1}=M\cdot r^{t}\)
停止条件:\(\left | r^{t+1}-r^{t} \right |_{1} <\varepsilon\)
其中\(\left | x \right |_{1}= {\textstyle \sum_{1}^{N}}\left | x_{i} \right |\)
是否收敛
不收敛的两种状况:
- Spider Trap 图中间有环路
- Dead end 有节点没有out-link
Spider Trap的Solution
每次随机游走都有两个选择,一个是按照链接随机访问,一个是在整体的图里随机跳到一个页面上
Dead End的Solution
到达没有出边的节点时,有100%的概率随机移动
最后综合起来,解决方案就是:
\(r_{j}^{}=\sum_{i\longrightarrow j}\beta \frac{r_i}{d_i}+(1-\beta ) \frac{1}{N}\)
Google Matrix
\(G=\beta M+(1-\beta )\left [ \frac{1}{N} \right ]_{N\times N}\)
那么power method仍然适用
r=G\(\cdot\)r
Poximity on Graphs
Personalized PageRank可以用来衡量节点与跳转节点集合S中的节点的相似性
Random Walk With Restarts
PageRank,Personalized PageRank,Random Walk With Restarts 的区别
- PageRank:跳转可以跳转所有的节点,并且每个节点有相同的概率被选中
- Personalized PageRank 跳转只能跳转到指定的节点集,集合中每个节点被选中的概率可以不同
- Random Walk With Restart只能跳转到起始节点
Random Walk
每个节点都有相同的重要性
每条边的重要性分布是均匀的
然后开始模拟随机游走
- 随机游走到一个邻居,并且记录访问的次数
- 然后以alpha的概率进行游走的重启
- 结束随机游走后,除起始节点外访问次数最多的就和起始节点有最高的相似性,分数越高,则相似度越大



