图形1.2.2 矩阵计算
矩阵计算
乘算
两个矩阵进行相乘的条件为：前一个矩阵的列数量等于后一个矩阵的行数量。
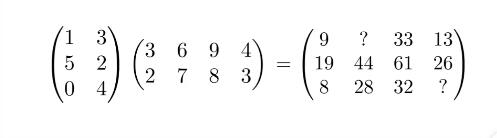
如：3行2列的矩阵A 与 2行4列的矩阵B 相乘得到的矩阵C为3行4列
对于矩阵的C的每个数C(m,n)等于行Am与列Bn相乘的结果
：C(2,4)=A2 · B4=A(2,1)·B(1,4) + A(2,2)·B(2,4)=5×4 + 2×3 = 26
该运算不满足交换律。
向量也能被认为是一个1行或者1列的矩阵
单位矩阵
单位矩阵是一个只有对角线是非零元素的矩阵
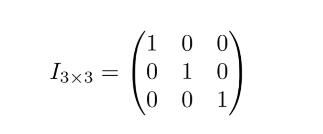
矩阵A与单位矩阵I的乘积结果等同于单位矩阵I与矩阵A的乘积结果
若存在矩阵B，使得AB和BA的乘积都是一个单位矩阵，那么该矩阵B则叫做A矩阵的逆，记作A-1，且我们称这两个矩阵是互逆的。
注意(AB)-1 = B-1A-1
对于一个进行了仿射变换矩阵A的图像，如果我们使用A矩阵的逆，对它进行A-1的仿射变换，它就会变成进行仿射变换矩阵A操作前的样子
转置
将矩阵的行与列互换。
对于矩阵A的转置矩阵记为AT
注意(AB)T = BTAT
加算与数乘
对于行数和列数都相等的矩阵，我们称其为同型矩阵。
矩阵的加算只能在同型矩阵间进行，在对应的行列位置进行加算。
矩阵能与常数k相乘，具体运算为矩阵内的每个数都与k进行乘算。
变换
缩放变换
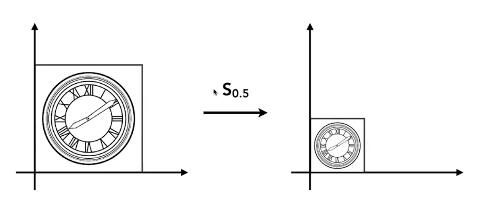
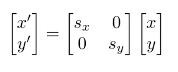
对于该单位矩阵我们称其为缩放矩阵，x' = sxx，y'=syy，对应的s就是缩放的倍率。
在存在s为负值的情况下，对应着将目标往对应的该轴反方向进行同等的缩放变换。
如sx为-1，sy为1的情况，则会将目标沿x轴水平对称生成缩放变换的结果。
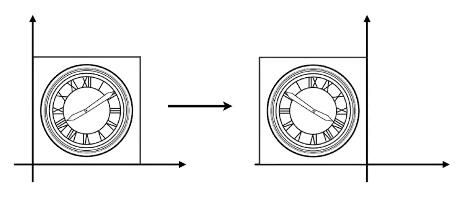
对于一种特殊的切变缩放变换，我们则根据其切变的位移量来得出对应的缩放矩阵。
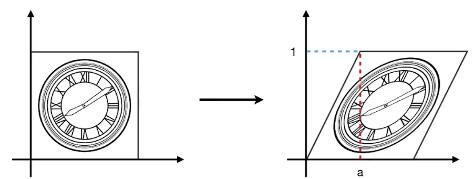
如图可知其x轴y轴均没有做大小上的变换，但是x轴为1的水平方向上，目标图片都偏移了a值的量，在x轴为0的水平方向上目标图片则没有偏移。即水平移动的偏移值为ay。
其缩放变换形式如下：
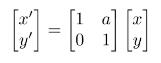
旋转变换
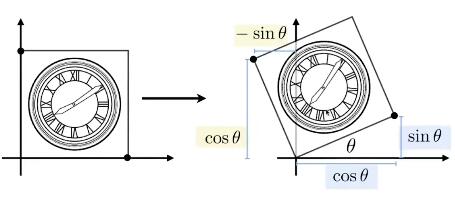
当目标旋转Θ角后，可看到目标图片的左下角的点没有位移，右下角的点从(1,0)变换到了(cosΘ,sinΘ)，左上角的点从(0,1)变换到了(-sinΘ,cosΘ)。
即变换矩阵A满足
A(1,1)·1 + A(1,2)·0 = cosΘ, A(2,1)·1 + A(2,2)·0 = sinΘ
A(1,1)·0 + A(1,2)·1 = -sinΘ, A(2,1)·0 + A(2,2)·1 = cosΘ
即可推导出变换矩阵A为
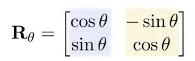
齐次坐标与位移变换
为了适配位移变换，我们引入了齐次坐标。
对于每个3维的点，我们将其新扩展一栏(x,y,z,1)T
通过这种方法，所有的线性变换都可以转换为仿射变换。通过这种方法，使用与前面一样的矩阵乘积可以将各种变换无缝地集成到一起。
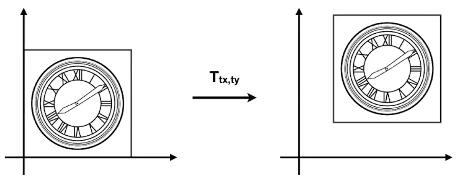
即该x' = x + tx，y'=y + ty。
我们可以由此写出位移变换矩阵
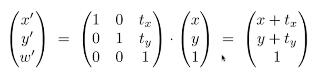
我们由上面的线性变换例子可以看到，这些变换的本质都是使用了矩阵的乘算操作来进行。根据矩阵的结合律，我们可以先把这些变换矩阵乘算到一起得到一个复合变换的矩阵。即我们能用一个它们的同型矩阵来储存一连串的变换
3维变换矩阵的示例
3维缩放矩阵和平移矩阵
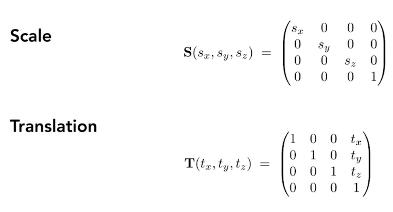
3维的旋转矩阵
参考
GAMES101-现代计算机图形学入门-闫令琪-Lecture 03 Transformation
