圆方树＆仙人掌学习笔记
仙人掌
定义
任意一条边只会出现在一个环里面的无向图（不一定连通）
解决工具：（狭义）圆方树
定义
把原图分成两类点，一类是圆点，一类是方点。如果一条边在仙人掌中不属于任何一个环中，那么它直接圆方树中的两个圆点。对于仙人掌中的任意一个环，每个环上的点在圆方树上对应的圆点向这个环对应的方点连边。
它把原图变成了一棵树。如何证明是一棵树：分别证明连通性和\(|E|=|V|-1\)即可。
构建
对于原图割边直接连圆圆边，对于环则用Tarjan把每个环抠出来即可，环的起点即\(\rm dfn\)序最小的点。具体看代码：
void tarjan(int x, int p)
{
low[x] = dfn[x] = ++ ind;
for (int i = hd[x]; i; i = nxt[i])
{
int y = to[i], z = w[i]; if (i == p || i == (p ^ 1)) continue;
if (!dfn[y]) pre[y] = z, f[y] = x, tarjan(y, i), low[x] = min(low[x], low[y]);
else low[x] = min(low[x], dfn[y]);
if (low[y] > dfn[x]) g.add(x, y, z), g.add(y, x, z); // 圆圆边
}
for (int i = hd[x]; i; i = nxt[i])
{
int y = to[i], z = w[i];
if ((dfn[y] > dfn[x]) && (f[y] != x)) Add(x, y, z); // 新建一个方点，连圆方边；此处x即为环的起点，而y是终点；通过不断跳fa即可找出当前环的所有点
}
return;
}
性质
- 没有方方边
- 是一颗无根树，形态与根的选取无关
例题
仙人掌上两点最短路
建圆方树。圆圆边连原边权，圆方边分类讨论：若是环的起点，连边权为\(0\)；否则连该点再环上到环的起点的最短路。
建出圆方树后，找到\(u,v\)的\(\rm {lca}\)为\(p\)，同样分类讨论：
- 若\(p\)为圆点，则答案就是树上两点的距离
- 若\(p\)为方点，则找到与\(p\)相连的两点\(a,b\)且分别是\(u,v\)的祖先。显然\({\rm{dis}}(a,u)\)和\({\rm{dis}}(b,v)\)也可以直接求，而\({\rm{dis}}(a,b)\)在环上直接算即可。
仙人掌上直径
建出圆方树。记\(f_x\)表示在以\(x\)为根的子树中以\(x\)为起点的最长链长度。
对于圆圆边，同树形dp的直径求法，有
对于圆方边，我们把环上的点拿出来（断环成链），对环dp后贡献到环的起点上即可。记\(len\)为环长，\(x\)为起点，有
总结
仙人掌上dp有点类似于基环树dp，即圆圆边就按照树上的方法正常dp，对于一个环就用整个环上的dp值更新起点的dp值，此时一般可以断环成链。
广义圆方树
定义/性质
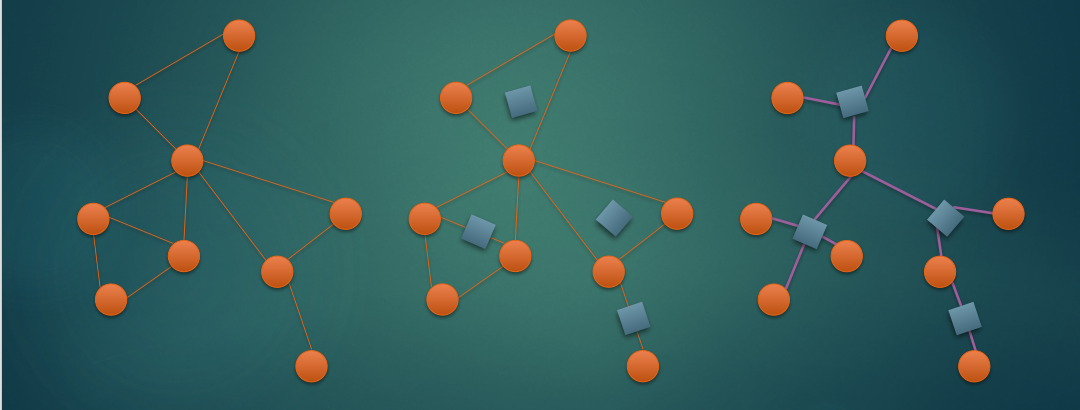
（图源yyb's blog）
只有圆方边，对于每个点双新建一个方点，最多只有\(2n-1\)个点的一棵树。代码：
void tarjan(int x, int p)
{
dfn[x] = low[x] = ++ ind; q[ ++ tt] = x;
for (int i = hd[x]; i; i = nxt[i])
{
int y = to[i]; if (i == p || i == (p ^ 1)) continue;
if (!dfn[y])
{
tarjan(y, i), low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x])
{
now ++ ; int o;
do {o = q[tt]; tt -- ; g.add(now, o), g.add(o, now);} while (o != y); // 注意不是o != x
g.add(now, x), g.add(x, now);
}
}
else low[x] = min(low[x], dfn[y]);
}
return;
}
例题
CF487E
看到“\(u\)到\(v\)的所有路径”，想到建圆方树。将方点的权值表示为点双中的最小圆点的权值，那么直接树剖套线段树即可。修改的话可以对每个方点维护一个\(\rm multiset\)维护与之相邻的所有圆点，每修改一个圆点就遍历与之相邻的所有方点修改即可。
但这样会被菊花图卡成\(n^2\)的，考虑优化。我们让方点的\(\rm multiset\)只存儿子圆点的权值，那么修改一个圆点时，就只需要改它父亲的\(\rm multiset\)。询问时只需要特判当\(\rm lca\)为方点时，要对其父亲的权值取\(\rm min\)。复杂度\(\mathcal{O}(n\log^2 n)\)。
总结
广义圆方树的应用场景一般有：
- 和割点有关
- 和路径的并有关（原图上\(u\)到\(v\)的所有路径的并可以用圆方树上\(u\)到\(v\)的路径表示，当然这要求题目所求是可并的，如取\(\rm min\)等，不能是加减之类的运算）。这是因为\(u\)到\(v\)路径上遇到的每个点双都有若干种走法（如环就有两种），把这个点双的信息表示在方点上即可表示这些路径的并。
解题思路有：
- 和其他数据结构结合（虚树、树剖等）
- 分别给圆点和方点赋上合适的点权，方点一般根据题目的性质赋上和该环上的所有圆点有关的点权
