T208925 塔顶试探（probe）

【题意】

给定一个01序列，求有多少个互不相同的树的欧拉序为这个序列（每次进入和回溯都记录在序列中）

【分析】

显然这是一个树的计数问题，24分的部分分就是给暴力dfs统计的

考虑对于$n\leq300$的情况该怎么处理

计数问题比较常见的方法有数学推式子，dp类型，容斥类......

这道题目的数据范围也在提示我们向dp靠拢

我们考虑设计状态f[i][j]表示序列i-j部分的方案数

我们发现这个问题有可以区间合并的性质，即i-k-1形成的树形结构和k-j的树结构可以通过拼凑来对i-j产生贡献

那么我们考虑如何转移

f[l][r] 可以由f[l][k]和f[k+1][r]转移而来 表示先走完l+1-k-1是l的子树的一部分，然后从k-r走l的另一棵子树最后回来

显然r-l一定要是偶数才可以，且l和r是一个节点

 

 

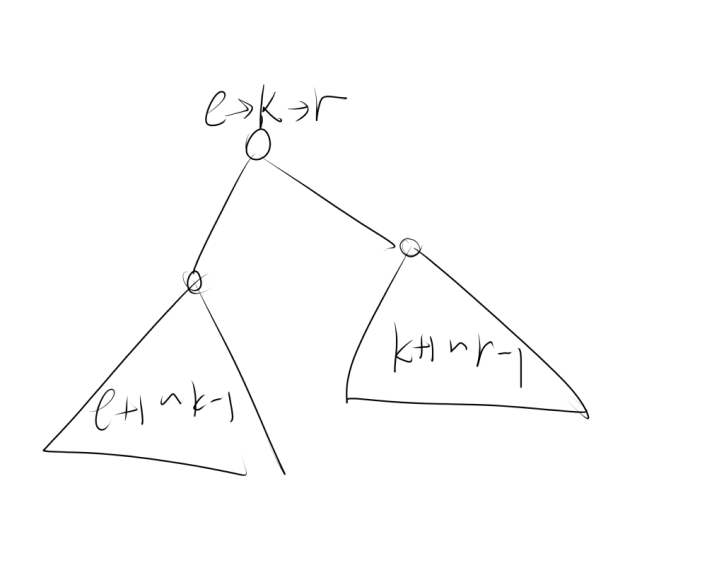
【分析】

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9;
ll f[305][305];
char s[305];
int n;
int main()
{
    freopen("probe.in","r",stdin);
    freopen("probe.out","w",stdout);
    scanf("%s",s+1);
    n=strlen(s+1);
    for(int i=1;i<=n;i++) f[i][i]=1;
    for(int len=3;len<=n;len+=2)
        for(int l=1;l+len-1<=n;l++)
        {
            int r=l+len-1;
            if(s[l]!=s[r]) continue;
            f[l][r]=f[l+1][r-1];
            for(int k=l+2;k<=r-2;k++)
                if(s[l]==s[k])
                    f[l][r]=(f[l][r]+f[l+1][k-1]*f[k][r]%mod)%mod;
        }
    printf("%lld\n",f[1][n]);
    return 0;
}