【数论 分治】poj 1845 Sumdiv

Sumdiv

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 37483		Accepted: 9161

Description

Consider two natural numbers A and B. Let S be the sum of all natural divisors of A^B. Determine S modulo 9901 (the rest of the division of S by 9901).

Input

The only line contains the two natural numbers A and B, (0 <= A,B <= 50000000)separated by blanks.

Output

The only line of the output will contain S modulo 9901.

Sample Input

2 3

Sample Output

15

Hint

2^3 = 8.
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).

 

 

 

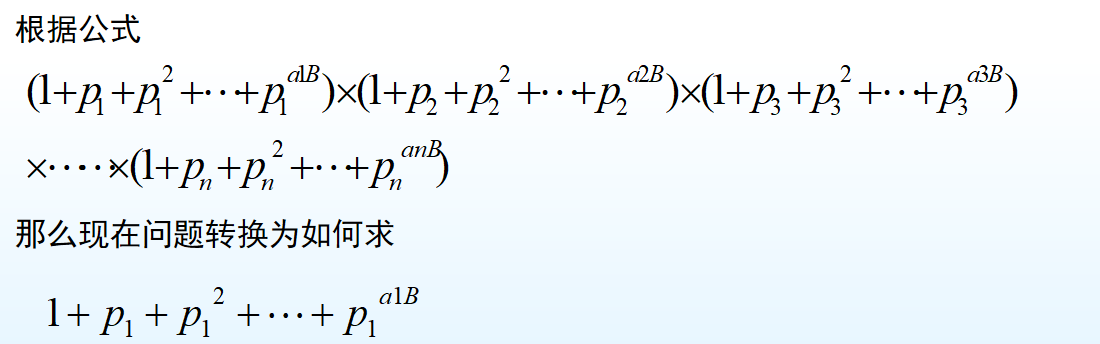
可以考虑分治来计算这个式子

 

 

 

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int mod=9901;
typedef long long ll;
ll qpow(ll a, ll b)
{
    ll res=1;
    if(!b) return 1;
    while(b)
    {
        if(b&1) res=(res*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return res;
}
ll dfs(int base,int step)
{
    if(step==0) return 1;
    if(step & 1) return dfs(base,step/2)*(qpow(base,(step+1)/2)+1)%mod;
    else return (dfs(base,step/2-1)*(1+qpow(base,step/2+1))%mod)+qpow(base,step/2)%mod;
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    int A,B;
    while(scanf("%d%d",&A,&B)!=EOF)
    {
        int cnt=0;
        ll res=1;
        for(int i=2;i*i<=A;i++)
        {
            cnt=0;
            while(A%i==0)
            {
                cnt++;
                A/=i;
            }
            res=res*dfs(i,cnt*B)%mod;
        }
        if(A>1) res=res*dfs(A,B)%mod;
        printf("%lld",(res+mod)%mod);
    }
    return 0;
}