2-3-数据结构-线性结构-顺序表 链表和哈希表
线性表
线性表是最基本的数据结构之一,在实际程序中应用非常广泛,它还经常被用作更复杂的数据结构的实现基础。
根据线性表的实际存储方式,分为两种实现模型:
- 顺序表,
- 链表,
下面分别进行研究,
顺序表的研究
顺序表的基本形式,数据元素本身连续存储,
第一种情况:
如果顺序表的存储元素都是固定大小的,只需要一块空间,
第二种情况,
但是存储的每一个元素的大小不是全部固定的,比如列表中,可以是存储数字,但是也有字符串,等,
所以可以每一个值都是放到另外一个存储块中存储,然后把每一个存储块的地址按照顺序表存起来,
这种取值的时候,需要先找到地址,然后通过地址去找到存储块,找到具体的内容,
顺序表的实现,
比如存储8个元素,这个存储空间是一次性的向操作系统申请到的,
所以一个顺序表,除了要保存具体的存储内容以外,还需要一个表头,
表头需要两个信息一个是容量是多大也就是最大的存储信息,还有一个就是现在的存储内容,也就是现在存储了多少个元素了,
怎么把表头和信息存储到一起?
一种是存储在一起,这叫做一体式的存储,
一种是分开存储,这叫做分离式存储,在存储表头的时候加一个信息,就是存储内容的地址,也就是表头有三个了,容量,目前的存储数量,存储信息的地址,
一体式的存储和分离式存储,哪一个好?
读取:一体式的存储,直接跳过表头就可以读取了,分离式存储是多一步,先从表头获取到地址信息,然后到地址获取具体信息,
扩充数据:
一体式的存储容量是固定的,如果要多存储数据,必须要重新申请空白的空间,然后数据搬过来,表头也要搬过来,
分离式存储,表头不需要改,只需要地址指向新的地址就可以了,
所以为了考虑到数据的动态变化,还是更多的采用的是分离式的存储,
扩充的时候如何预估申请的空间呢?
比如原来的空间只能存储4个元素,为了存储第5个元素, 我需要重新申请空间,
第一种方式,固定申请,比如每次再申请10个空间,就是14个,这种节省空间,但是操作频繁,
第二种方式,加倍的方式,一开始4个,下一次就是翻倍,就是8个,这种空间牺牲一些, 但是时间会更有效率,这就是空间换取时间,
顺序表的弊端也很明显了,就是每次扩充数据,都需要重新申请空间,那么有没有一种结构,多一个数据,就往上加,而不是重新申请空间呢?
那就是链表了
链表的研究
一个列表,需要存储3个元素,200,300,400
不用顺序表,这种受限,所以采用每加一个元素就申请一个空间,然后在每一个元素的后面新开一个空间,用来指向另外一个元素,
这样层层链接,就可以了,这种就是链表,
链表如何实现:
链表中每一个元素都是一个对象,每一个对象都是一个节点,包含有数据域key和指向下一个节点的指针next。通过各个节点之间的互相连接,最终串联成一个列表
每一个元素保持两个内容,准确来讲不能叫做元素了,而是叫做节点,
- 一个是信息,叫做数据区,
- 一个是下个元素的链接地址,这叫做链接区,尾结点指向的区域就是指向空,
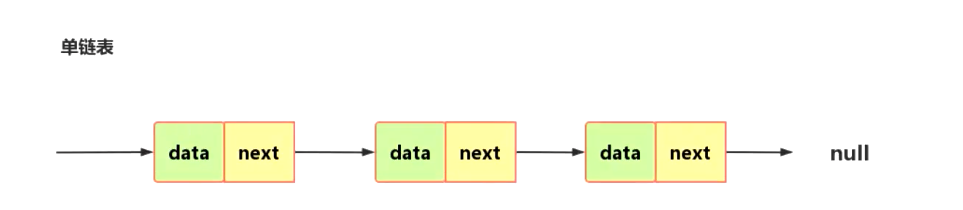
- 每一个节点有两个属性,data和next,
- data可以是各种数据
- next是下一个节点,
- 所以头指向的是第一个节点,尾部指向的事null,
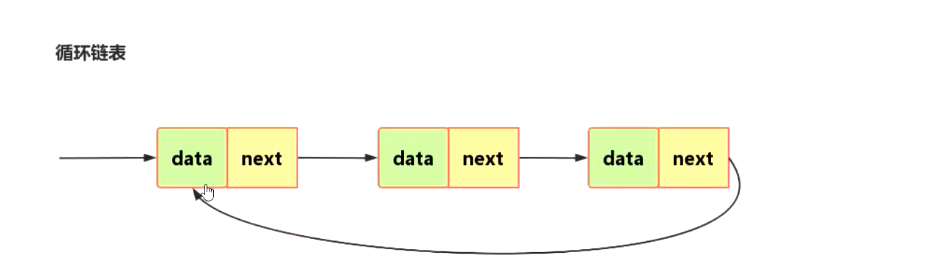
- 你看循环链表和单链表的唯一区别就是尾部指向的不是null,而是第一个节点,

- 双向链表,每一个节点有三个部分,prev,data,next,prev指向的是前一个节点,
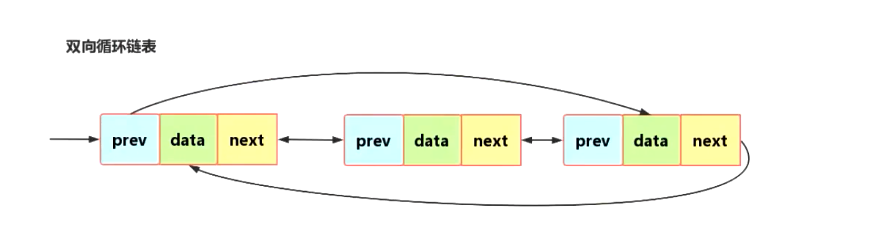
- 明白了前面的循环链表,就明白了这个双向循环链表了,就是首尾都是指向的
- 头指向尾,尾指向头,
双向链表和单链表的区别
- 很明显单链表找一个节点的前面一个节点,是需要从头还是找的,而双向链表很容易就可以找到,
- 但是双向链表很明显费空间,所以这是空间换时间的概念,
链表和列表有什么区别???
1,存储方式
列表是一种连续的存储结构,它在内存中分配一段连续的空间来存储元素,每个元素占用固定的空间。因此,列表的访问速度非常快,可以通过下标来直接访问任意位置的元素。
链表是一种离散的存储结构,它不需要一段连续的空间来存储元素,而是通过指针来连接一系列的节点。每个节点含数据和指向下节点的指针。因此,链表的访问速度比较慢,需要从头节点开始遍历,直到找到目标节点。
2,插入和删除,查询的差异
- 列表是连续的,但是链表不是连续的,链表没有索引,列表有索引,
- 因为列表是连续的存储结构,列表插入的时候后面的元素都要往后移动位置,所以这些操作的时间复杂度为O(n),但是链表插入是简单的,就是指向问题就好了,O(1)
- 列表查询的时候可以使用索引,O(1),但是链表查询就要从头往后开始查了,O(n),
3,空间占用
列表在内存中分配一段连续的空间来存储元素,因此它的空间占用比较大。而链表不需要一段连续的空间来存储元素,它的空间占用比较小。
单向链表,
第一节点是头节点,第二个节点是尾结点,
Python中交换变量的操作,
a=10
b=10
a,b=b,a # 这就是交换,这只在Python中有,别的语言没有,
为什么能达到这个效果,本质是什么?
a是一个空间,10是一个空间,a的空间指向10的空间,
所以这种交换,就是指向的变化,所以不是真正的赋值
所以要记住,Python中的变量不是保存的内容,而是保持的地址,地址指向的地方保存的才是具体的信息,
所以a只是等于数字,字符串,列表等,这就是因为这个变量就是一个指向,这是Python和其他语言的差异,
python实现单向链表
class SingleNode(object):
# 里面有两个元素
def __init__(self,elem):
self.elem=elem
self.next=None # 因为一开始只有一个元素,我不知道下一个元素是什么,
# 第一步:创建一个新的链表
# sll=SingleLinkList(),这里面是空的,没有任何的节点,head----指向None,
# 第二步:现在链表有了,要保存一个整数值100,就要构造一个节点,
# node=SingleNode(100) # 这里面包含两个值,就是100,none,然后链表的head就不是none,就是第一个节点,
class SingleLinkList(object):
"""单链表"""
def __init__(self,node=None):
self.__head = None # 私有属性 设置成空,就是说这个链表里面没有任何的节点,先
def is_empty(self):
"""判断链表是否为空"""
return self.__head == None # 只要链表的head是none就是空的链表,
# 如何实现这个长度,因为链表是 head----100,next---20,next---300,next---none
# 所以遍历这个链表,如果next是none就到头了,
def length(self):
"""链表长度"""
# cur游标,用来移动遍历节点,
cur = self.__head
# count用来计数,
count = 0
# 尾节点指向None,当未到达尾部时
while cur != None:
count += 1
cur = cur.next # 将cur后移一个节点,这一句很关键,
return count
def travel(self):
"""遍历链表"""
cur = self.__head
while cur != None:
print(cur.elem,end=" ")
cur = cur.next
# 在头部插入数据的逻辑
# 第一步,把新元素的next指向第一个节点,
# 第二步,把head指向这个新元素
# 这个逻辑也是可以处理空链表的情况,
def add(self, item):
"""头部添加元素"""
# 先创建一个保存item值的节点
node = SingleNode(item)
# 将新节点的链接域next指向头节点,即_head指向的位置
node.next = self.__head # 这个__head是原来的头部节点,
# 将链表的头_head指向新节点
self.__head = node
def append(self, item):
"""尾部添加元素"""
node = SingleNode(item)
# 先判断链表是否为空,若是空链表,则将_head指向新节点
if self.is_empty():
self.__head = node
# 若不为空,则找到尾部,将尾节点的next指向新节点
else:
cur = self.__head
while cur.next != None:
cur = cur.next # 这个是一个属性,保存了一个节点类对象了,通过一通遍历,就把cur变成了尾结点了,
cur.next = node # 这就是把尾结点的指针指向下一个节点,
# 通过坐标插入的实现逻辑
# inset(2,300)
# 第一步,让新的节点,指向原来节点是2的节点,
# 第二步,让左边是1的节点,指向新的节点,
# 因为传过来的坐标是用户使用的,所以需要控制,
# 1,如果是传入的0
# 2,如果是传入的比长度还要大
def insert(self, pos, item):
"""指定位置添加元素"""
# 若指定位置pos为第一个元素之前,则执行头部插入
if pos <= 0:
self.add(item)
# 若指定位置超过链表尾部,则执行尾部插入
elif pos > (self.length() - 1):
self.append(item)
# 找到指定位置
else:
node = SingleNode(item)
count = 0
# pre用来指向指定位置pos的前一个位置pos-1,初始从头节点开始移动到指定位置
pre = self.__head
while count < (pos - 1):
count += 1
pre = pre.next # 如果pos是2,那这个pre.next就是原来坐标是2的节点,
node.next = pre.next # 新节点node的next指向插入位置的节点
pre.next = node # 将插入位置的前一个节点的next指向新节点
# 传入一个数据,需要删除具体的数据,
# 实现逻辑,
# 需要把删除的节点的上一个节点的指针指向下一个节点,让这个链表连接起来,
# 用两个游标来解决这个问题,
# 1,cur游标指向head
# 2,pre游标指向cur,
# 3,cur指向cur.next
def remove(self, item):
"""删除节点"""
cur = self.__head
pre = None
while cur != None:
if cur.elem == item: # 找到了要删除的元素
if cur == self.__head: # 如果找到的要删除的节点正好是第一个节点,怎么判断是第一个节点?:cur == self.__head
self.__head = cur.next # 直接是让head指向被删除节点的next
else: #
pre.next = cur.next # 将删除位置前一个节点的next指向删除位置的后一个节点,这样的写法即使只有一个节点,也能实现,
break
else:
# 继续按链表后移节点,这两句就是把两个游标都往后移动,
pre = cur
cur = cur.next
# 实现逻辑
# 还是需要遍历列表的,判断节点的数据和用户要找的数据,是否相等,如果相等返回true,否则就是false,
def search(self, item):
"""链表查找节点是否存在,并返回True或者False"""
cur = self.__head
while cur != None:
if cur.elem == item:
return True
cur = cur.next
return False
if __name__ == "__main__":
ll=SingleLinkList()
print(ll.is_empty())
print(ll.length())
ll.append(1)
print(ll.is_empty())
print(ll.length())
ll.append(2)
ll.append(3)
ll.append(4)
ll.append(5)
ll.add(9)
ll.insert(-1,200)
ll.insert(1,300)
ll.insert(11,400)
ll.remove(400)
ll.travel()
实现单向链表,
逻辑:
- 因为链表的每一个节点,需要保存数据和链接,我们自己定义一个数据类型叫做节点类型来保存这两个信息,
- 定义一个单链表类,初始是没有节点的,head是空的
3,实现几个方法
判断是否为空,
返回链表长度
遍历
头部添加,
尾部添加
中间添加
删除节点,
查找,
双向链表
每一个节点需要保存三个内容了,上一个节点的地址,本个节点的数据,下一个节点的地址,
这样就有一个后继节点和前驱节点,
对于头结点的前驱节点是空,对于尾节点的下一个节点是空,
python实现双向链表
class Node(object):
"""双向链表节点"""
def __init__(self, item):
self.item = item
self.next = None
self.prev = None
class DLinkList(object):
"""双向链表"""
def __init__(self):
self.__head = None
def is_empty(self): # 和单链表是一样的,
"""判断链表是否为空"""
return self.__head is None # self.__head == None你可以使用双等号,但是pep8推荐使用is,
def length(self): # 和单链表是一样的,
"""返回链表的长度"""
cur = self.__head
count = 0
while cur != None:
count += 1
cur = cur.next
return count
def travel(self): # 和单链表是一样的,
"""遍历链表"""
cur = self.__head
while cur != None:
print(cur.item)
cur = cur.next
# 这个和单链表不一样,
# 你在头部新增了一个节点
# 第一步,新的节点的next指向下一个节点
# 第二步,新节点的等于head
# 第三步,原来的头部节点的prev指向新的节点,
def add(self, item):
"""头部插入元素"""
node = Node(item)
if self.is_empty():
# 如果是空链表,将_head指向node
self._head = node
else:
node.next = self.__head # 空链表的时候self.__head还是一个none,所以next是等于none的,
self.__head=node # 让头部节点等于这个节点,
node.next.prev = node # node.next这是原来的头节点,他的prev指向新节点
# 这个和单链表不一样,
# 第一步,原来的尾结点的next指向新的节点,
# 第二步,新的节点的prev,指向原来的尾结点,
def append(self, item):
"""尾部插入元素"""
node = Node(item)
if self.is_empty():
# 如果是空链表,将__head指向node
self.__head = node
else:
# 移动到链表尾部
cur = self.__head
while cur.next != None:
cur = cur.next # 这一步就是移动到尾节点
# 将尾节点cur的next指向node
cur.next = node
# 将node的prev指向cur
node.prev = cur
# 这个插入,和单链表不一样,
# 第一步,新的节点的next指向原来位置的节点,node.next = cur
# 第二步,新的节点的prev指向原来位置的上一个节点cur.prev,node.prev = cur.prev
# 第三步,原来位置的上一个节点的next指向新的节点,node,prev.next = node
# 第四步,原来位置的prev指向新的节点,cur.prev = node
# 代码不是唯一的,但是要理清楚,这种可能是面试题,可以画图理解,
def insert(self, pos, item):
"""在指定位置添加节点"""
if pos <= 0:
self.add(item)
elif pos > (self.length() - 1):
self.append(item)
else:
cur = self._head
count = 0
# 移动到指定位置的前一个位置
while count < pos:
count += 1
cur = cur.next
# 退出循环的时候,cur指向pos位置
node = Node(item)
node.next = cur # 第一步,新的节点的next指向原来位置的节点
node.prev = cur.prev # 第二步,新的节点的prev指向原来位置的上一个节点
node.prev.next = node # 第三步,原来位置的上一个节点的next指向新的节点
cur.prev = node # 第四步,原来位置的prev指向新的节点
# 和单链表的逻辑不一样,
# 第一步:让删除节点的上一个节点的next,指向删除节点的下一个节点,cur.prev.next = cur.next
# 第二步,让删除节点的下一个的prev,指向删除节点的上一个节点,cur.next.prev = cur.prev
# 如果是首节点,
# 第一步:让head等于当前节点的下一个节点
# 第二步:把当前节点的下一个节点的prev变成none,
# 只有一个节点的时候,
# 直接让head等于当前节点的next,因为当前节点的next是none,
def remove(self, item):
"""删除元素"""
cur=self.__head
while cur != None:
if cur.item == item:
if cur ==self.__head:
self.__head=cur.next
if cur.next: # 这是专门处理只有一个节点的时候,因为只有一个节点,cur.next.prev这是没有值的,
cur.next.prev=None
else:
cur.prev.next = cur.next # 将cur的前一个节点的next指向cur的后一个节点
if cur.next:
cur.next.prev = cur.prev # 将cur的后一个节点的prev指向cur的前一个节点
break
else:
cur=cur.next
def search(self, item):
"""查找元素是否存在"""
cur = self.__head
while cur != None:
if cur.item == item:
return True
cur = cur.next
return False
if __name__ == "__main__":
ll = DLinkList()
ll.add(1)
ll.add(2)
ll.append(3)
ll.insert(2, 4)
ll.insert(4, 5)
ll.insert(0, 6)
ll.travel()
ll.remove(1)
ll.travel()
python实现单向循环链表
# 单向循环链表,
# 和单向链表的唯一区别在于尾结点的next指向了头结点了,
class Node(object):
"""节点"""
def __init__(self, item):
self.item = item
self.next = None
class SinCycLinkedlist(object):
"""单向循环链表"""
def __init__(self,node=None):
self.__head = None
if node:
node.next=node # 只有一个元素也要指向自己,
def is_empty(self): # 和单链表一样,
"""判断链表是否为空"""
return self.__head == None
def length(self):
"""返回链表的长度"""
# 如果链表为空,返回长度0
if self.is_empty():
return 0
count = 1
cur = self.__head
while cur.next != self.__head: # 判断尾部的条件变了,如果一个节点的next是头部节点,这就是尾结点了,
count += 1
cur = cur.next
return count
def travel(self):
"""遍历链表"""
if self.is_empty():
return
cur = self.__head
while cur.next != self.__head:
print(cur.item)
cur = cur.next
# 退出循环,cur指向尾结点,但是尾结点的元素未打印,
print(cur.item) # 对于空节点,一个节点的情况也是能满足的,
# 逻辑
# 第一步,把新节点的next指向原来的头节点
# 第二步,把头结点指向到新节点,
# 第三步,把尾结点的next指向头结点,
# 如果是一个空的链表,
def add(self, item):
"""头部添加节点"""
node = Node(item)
if self.is_empty():
self.__head = node
node.next = self.__head
else:
node.next = self.__head # 添加的节点指向__head
cur = self.__head # 这是设置游标
while cur.next != self.__head:
cur = cur.next # 不断的往后移动
cur.next = node # 退出循环,cur就是指向了尾结点,将尾部节点的next指向node
self.__head = node # 把头结点指向到新节点,
# 逻辑
# 第一步,把新的节点的next指向head,
# 第二步,把原来的尾结点的next指向新节点,
def append(self, item):
"""尾部添加节点"""
node = Node(item)
if self.is_empty():
self.__head = node
node.next = self.__head
else:
# 移到链表尾部
cur = self.__head
while cur.next != self.__head:
cur = cur.next
cur.next = node # 将尾节点指向node
node.next = self.__head # 将node指向头节点__head
# 逻辑和单链表是一样的,
def insert(self, pos, item):
"""在指定位置添加节点"""
if pos <= 0:
self.add(item)
elif pos > (self.length()-1):
self.append(item)
else:
node = Node(item)
cur = self.__head
count = 0
# 移动到指定位置的前一个位置
while count < (pos-1):
count += 1
cur = cur.next
node.next = cur.next
cur.next = node
# 逻辑
# 如果删除的是头结点,
# 第一步,head指向删除节点的下一个节点
# 第二步,尾结点的next指向新的head,
# 如果不是头结点,
# 和单链表一样,直接把删除节点上一个节点的next指向,删除节点的下一个节点,
def remove(self, item):
"""删除一个节点"""
# 若链表为空,则直接返回
if self.is_empty():
return
cur = self.__head
pre = None
while cur.next != self.__head:
if cur.item==item:
if cur.next == self.__head: # 这是头结点的情况,
#如果是头结点还是需要遍历一遍,
rcur=self.__head
while rcur.next != self.__head:
rcur=rcur.next
self.__head = cur.next
rcur.next=self.__head
else: # 不是头结点的情况
pre.next=cur.next
return
else:
pre= cur
cur=cur.next
# 退出循环,cur指向尾结点,
if cur.item == item:
if cur ==self.__head:
self.__head=None
else:
pre.next = cur.next
# 和单链表不一样
def search(self, item):
"""查找节点是否存在"""
if self.is_empty():
return False
cur = self.__head
while cur.next != self.__head: # 这种遍历把尾部节点漏掉了,对尾结点单独处理一下,
if cur.item == item:
return True
else:
cur = cur.next
# 退出循环,cur指向的尾结点,
if cur.item == item: # 对尾节点进行判断,
return True
return False
# 所以你会发现整个过程,代码不是问题,都是最基本的,关键是要把逻辑理清楚,
# 你还可以对双向链表进行扩充,就是变成双向循环链表,
if __name__ == "__main__":
ll = SinCycLinkedlist()
ll.add(1)
ll.add(2)
ll.append(3)
ll.insert(2, 4)
ll.insert(4, 5)
ll.insert(0, 6)
ll.travel()
ll.remove(1)
ll.travel()
为什么要用python实现链表?
最近在学“python及其数据结构”,学完用python实现链表后感觉完全没有实用性啊,实属困惑,链表的功能用python自己的list不是都能实现吗?
网上的回答:学习链表之类的数据结构的关键不在于用什么语言实现,而是让你们理解,你所谓那些list等已经有的轮子底层是怎么实现的,
哈希表
哈希表(又称为散列表),是一种线性表的存储结构。哈希表由一个顺序表(数组)和一个哈希函数组成。哈希函数h(k)将k作为自变量,返回元素的存储下标。
哈希表在Python中的应用
a、字典与集合都是通过哈希表来实现的
b、 在Python中的字典:
a = {'name': 'Alex', 'age': 18, 'gender': 'Man'},使用哈希表存储字典,通过哈希函数将字典的键映射为下标。
c、在字典键值对数量不多的情况下,几乎不会发生哈希冲突,此时查找一个元素的时间复杂度为O(1)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号