3-1-基础算法-排序算法(冒泡排序,选择排序,插入排序,快速排序,归并排序)
排序算法
排序算法,
我们想要把线性表中的无序序列,排成有序序列,的算法,就是排序算法,
排序算法的稳定性
举例:假设对下面的元组要以他们的第一个数字来排序。
(4, 1) (3, 1) (3, 7)(5, 6)
如果你排序之后,(3, 1) (3, 7)和原来的顺序一样,就是稳定的,否则就是不稳定的,
(3, 1) (3, 7) (4, 1) (5, 6) (维持次序)
(3, 7) (3, 1) (4, 1) (5, 6) (次序被改变)
我们说排序就是默认从小到大的,
冒泡排序
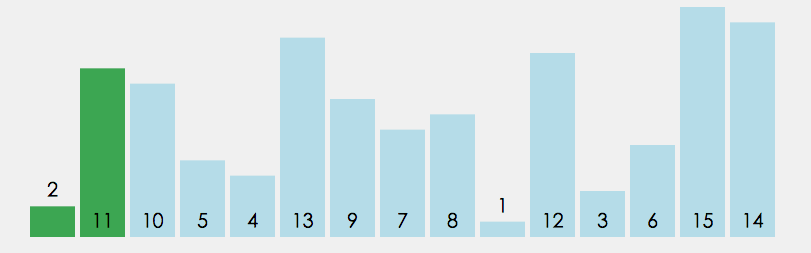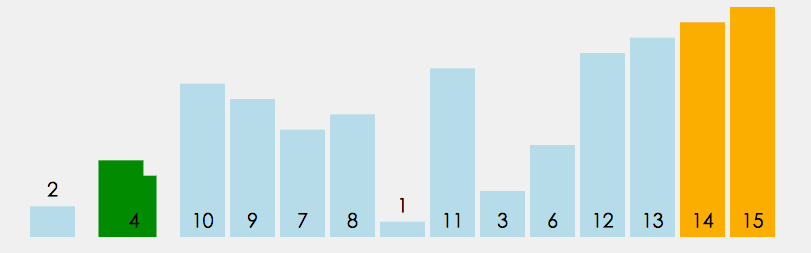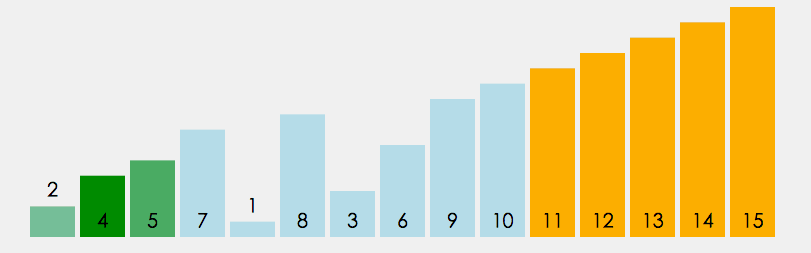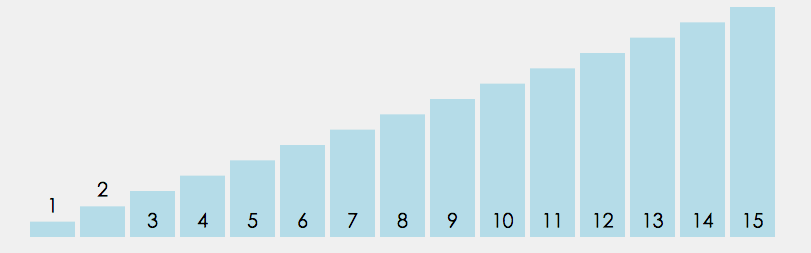
冒泡排序代码
# 假设n个元素待排序
# 1. 冒泡排序的步骤
# 1.1 从头到开始遍历列表进行交换元素
# 比较相邻两个元素,如果前面元素比后面元素大,则交换两个元素位置,将大的元素放到后面
# 从开始第一对元素到最后一对元素进行交换,最后的元素会是最大的数
# 1.2 重复第一步骤,总要进行n-1次;
def bubble_sort(arr):
# 遍历的次数
for i in range(1, len(arr)):
# 从头遍历到未进入排序的位置
for j in range(0, len(arr) - i):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
if __name__ == '__main__':
s = [9, 8, 6, 7, 4, 3, 99, 5, 3]
new_s = bubble_sort(s)
print(new_s)
# 稳定性:稳定
# 最优时间复杂度:O(n^2)
# 最坏时间复杂度:O(n^2)
代码实现逻辑解析
- 两个for循环
- 外层控制的是有多少个元素就循环多少次,
- 内层控制的是把第一个往后比较,一直移动到最后,
- 由于内层,每次循环都会排好一个最大的,所以每次循环都要减少一次,
难点就是range这个地方,先写内层循环,就是走一轮,外层循环控制走几轮,
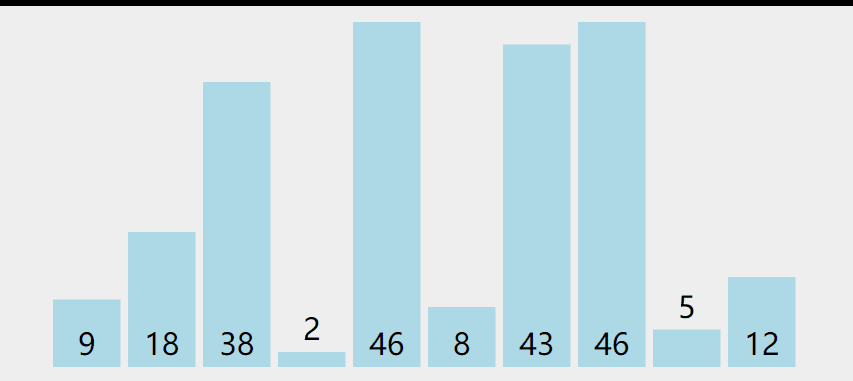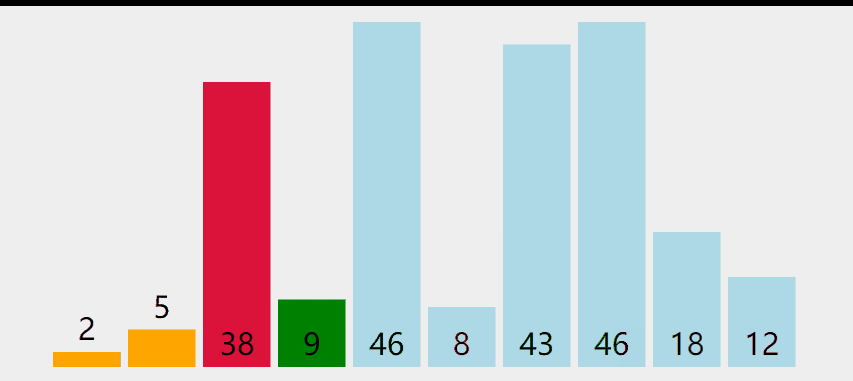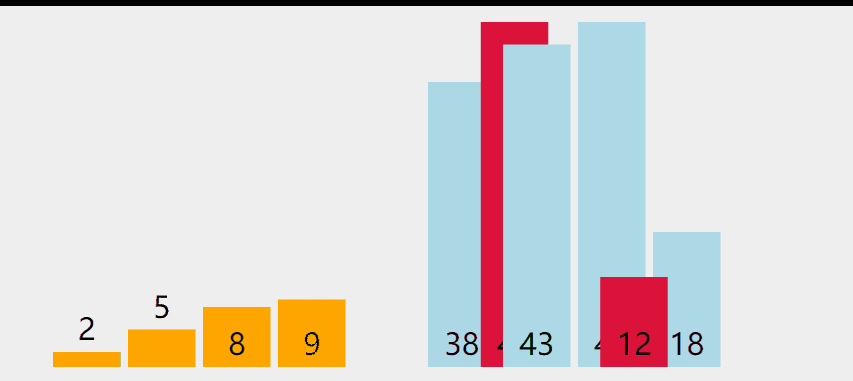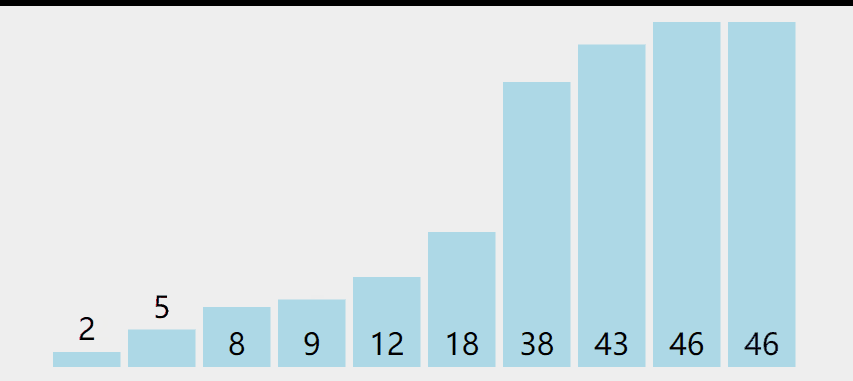
选择排序
# 假设n个元素待排序
# 1. 选择排序步骤
# 1.1 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
# 1.2 再从剩余未排序元素中继续寻找着最小(大)元素,然后放到已排序的末尾。
# 1.3 重复第二步,直到所有元素排序完毕
def select_sort(arr):
# 待插入的位置
for i in range(0, len(arr)):
# 从待排序位置查找最小(大)值放到待插入的位置
min_index = i # 记录最小数的索引
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
min_index = j
# i不是最小数时,将i和最小数进行交换
if i != min_index: # 这个判断可有可无,没有也不影响结果
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
if __name__ == '__main__':
s = [9, 8, 6, 7, 4, 3, 99, 5, 3]
new_s = select_sort(s)
print(new_s)
# 稳定性:稳定
# 最优时间复杂度:O(n^2)
# 最坏时间复杂度:O(n^2)
插入排序
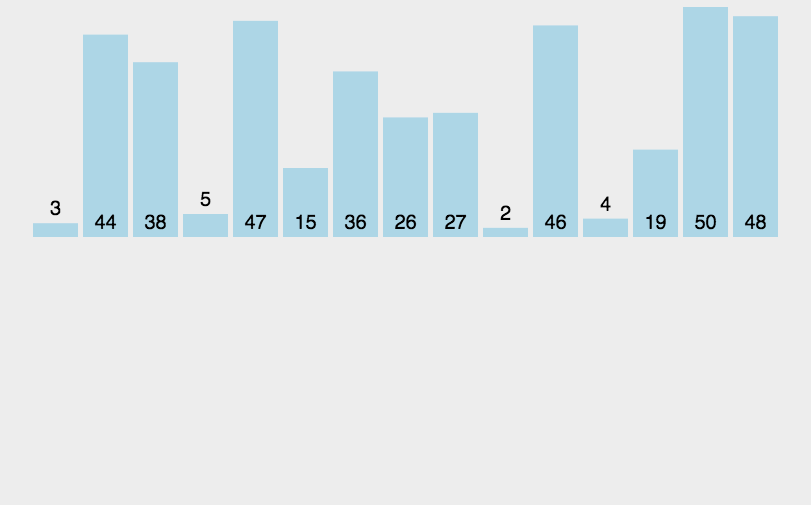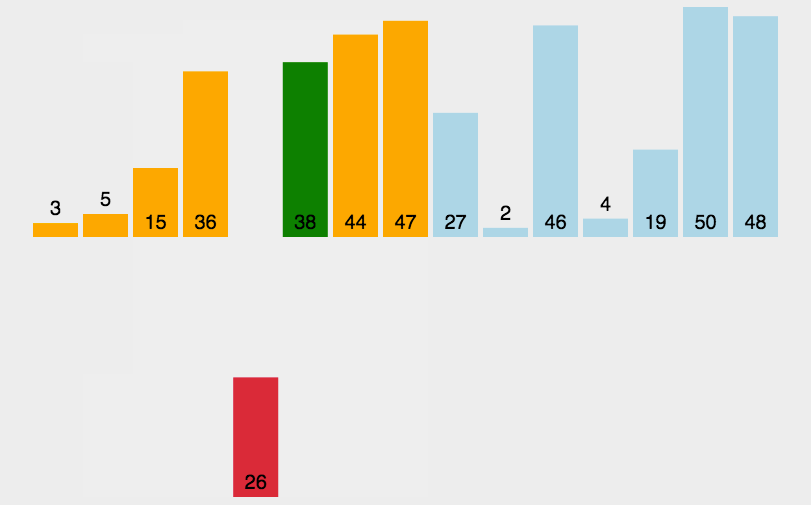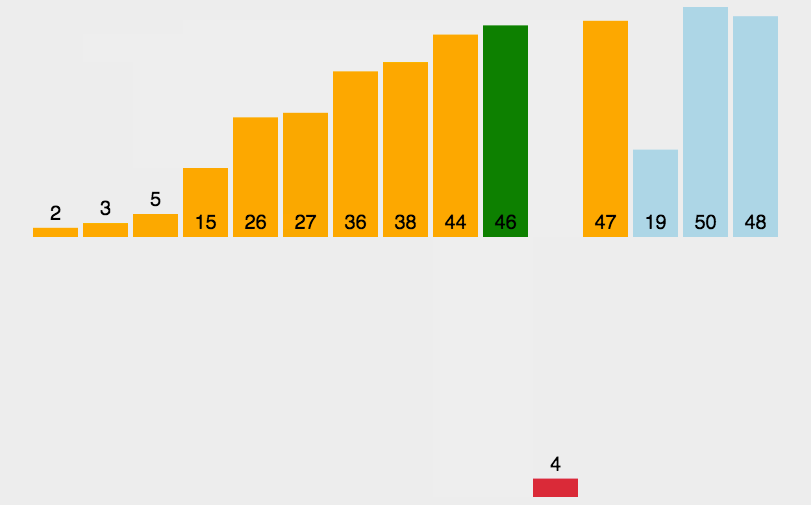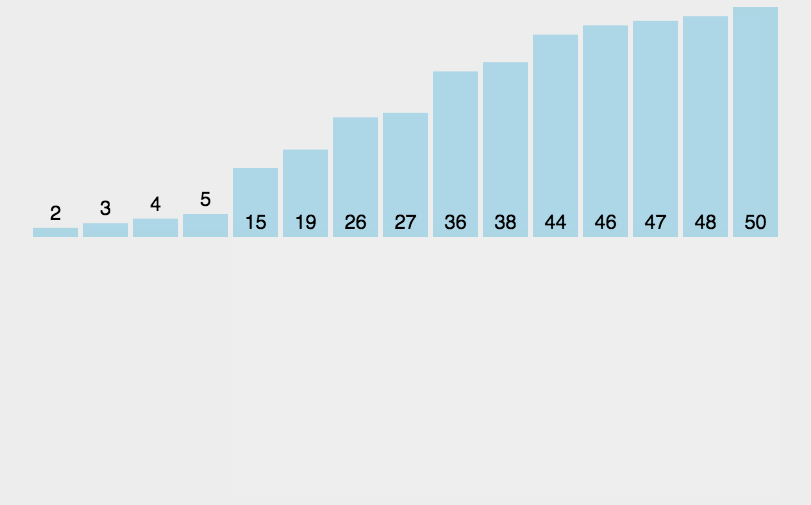
# 假设n个元素待排序
# 1. 插入排序步骤
# 1.1 将第一个元素看作有序序列,把第二个元素到最后一个元素当成是未排序序列
# 1.2 从未排序的初始位置开始扫描到结尾,将未排序的元素插入到有序序列的适当位置。
def insert_sort(arr):
# 待插入的元素
for i in range(len(arr)):
preIndex = i - 1 # 已经排好序的最后一个位置
current = arr[i] # 存储待插入的元素
while preIndex >= 0 and arr[preIndex] > current:
arr[preIndex+1] = arr[preIndex] # 将元素向后移
preIndex -= 1
arr[preIndex+1] = current
return arr
if __name__ == '__main__':
s = [9,8,6,7,4,3,99,5,3]
new_s = insert_sort(s)
print(new_s)
# 稳定性:稳定
# 最优时间复杂度:O(n^2)
# 最坏时间复杂度:O(n^2)
快速排序
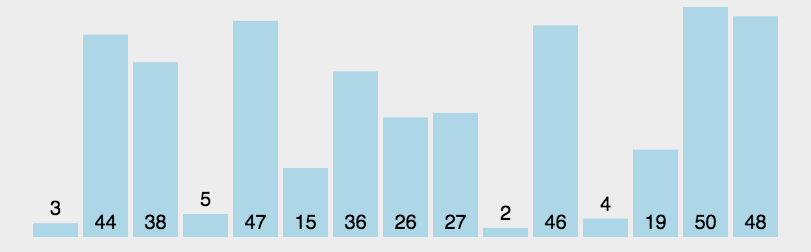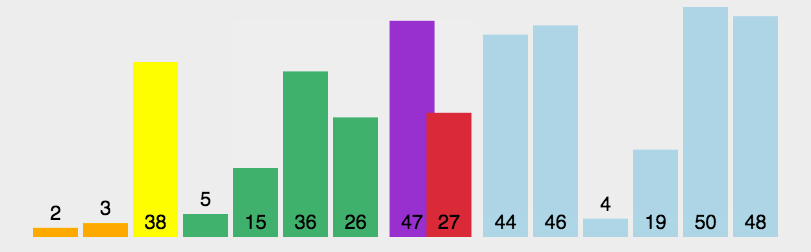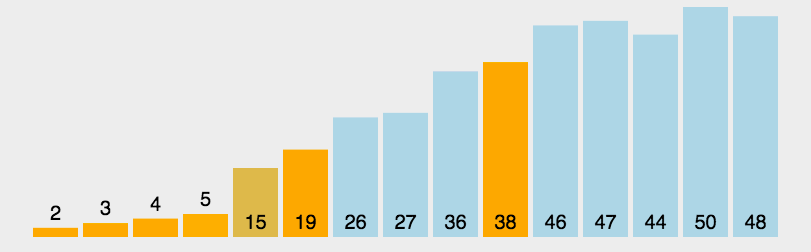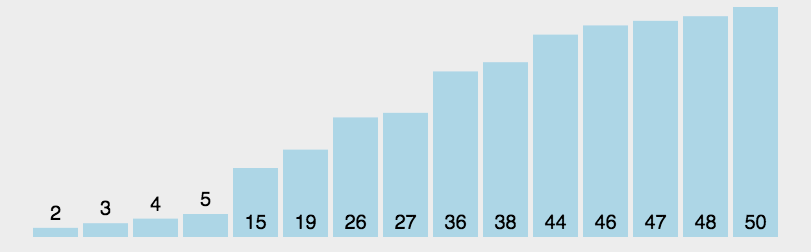
# 快速排序的思路
# 快速排序在排序时主要进行两步操作。
# 1,随机选取一个基准值,随机值可以选择第一个值,
# 2,将所有数据和基准值对比,将大于基准值的数据放入基准值右侧,小于基准值的数据放入基准值左侧
# 在左右两侧再次选择基准值重复上述操作。(可选择递归或栈的方式)
# 递归到最底部的判断条件是数列的大小是零或一,此时该数列显然已经有序。
def quick_sort(alist, first, last):
if first >= last: # 递归的退出条件
return
pivot = alist[first] # 列表的第一个元素,alist[first]作为基准值
left = first # 通过两个游标,left,right
right = last
# 一轮循环,有可能,不能将所有的大数都放到基准值的右边,小数放到基准值的左边,所以直到left>right 跳出循环;
while left < right:
# 找寻右边数列比基准值小的数的位置
while left < right and alist[right] >= pivot:
right -= 1
alist[left] = alist[right]
# 找寻左边数列比基准值大的数的位置
while left < right and alist[left] < pivot: # 如果符合条件,left游标就一直右移,不需要移动
left += 1
alist[right] = alist[left]
# 将大的数放在基准值的右边,小的数放在基准值的左边
# while结束时候,left=right ,将基准值放到中间
alist[left] = pivot
quick_sort(alist, first, left - 1) # 递归处理
quick_sort(alist, left + 1, last) # 递归处理
if __name__ == '__main__':
alist = [9, 8, 6, 7, 4, 3, 99, 5, 3]
quick_sort(alist, 0, len(alist) - 1)
print(alist)
# 稳定性:不稳定
# 最优时间复杂度:O(nlogn)
# 最坏时间复杂度:O(n^2)
归并排序

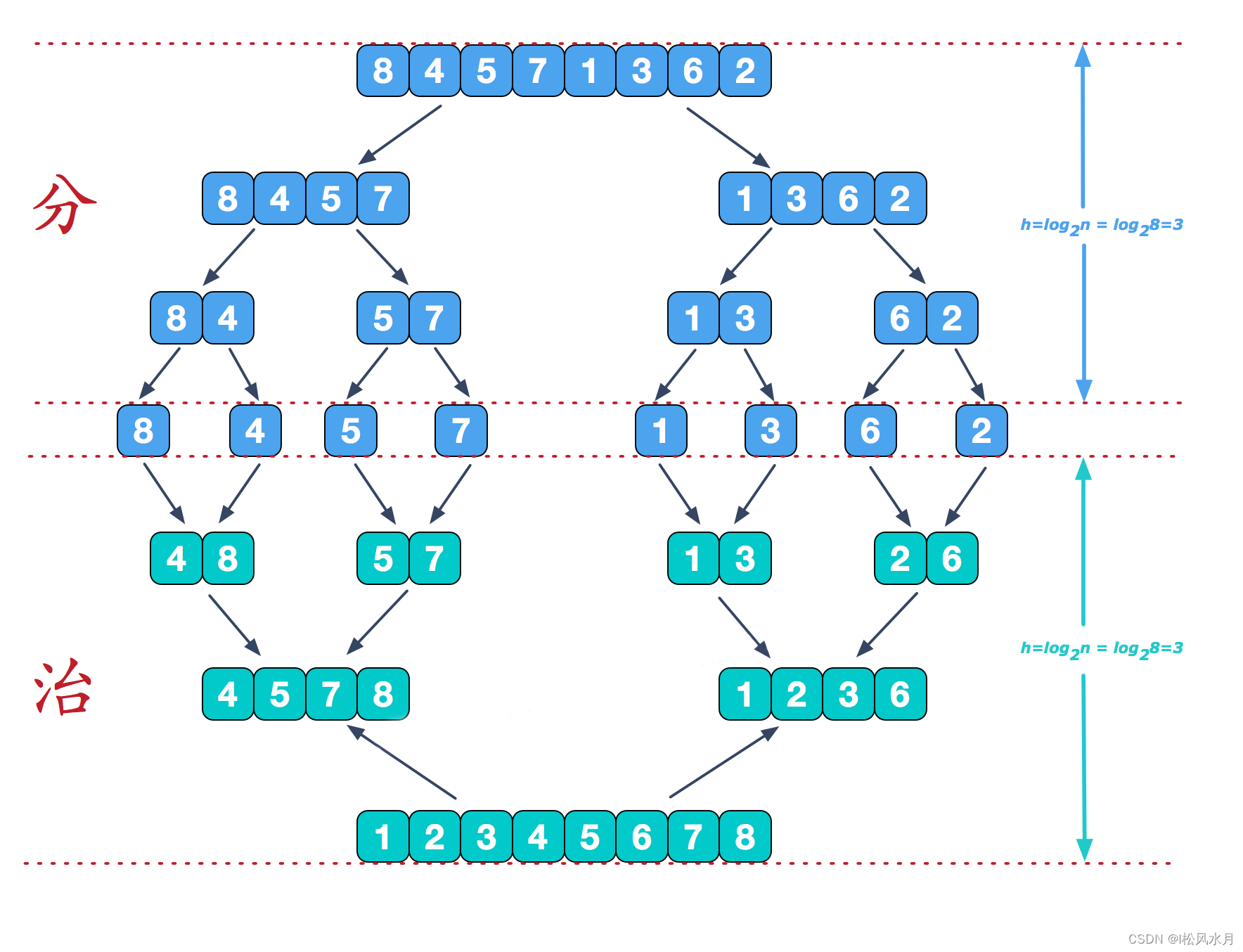
# 归并排序思路
# 两步:
# 第一步,拆分
# 对整个序列进行拆分,左边一部分,右边一部分
# 然后对每一部分再次进行拆分,一直到拆分到只有一个元素,就到头了,
# 第二步,合并
# 然后把拆分到的再次合并,小的在前,大的在后,
# 所以叫做归并,因为有一个拆分合并的过程
# 还是要用到递归的,
def merge(L_list, R_list): # 拼接
# 记录左右列表中元素位置情况
i, j = 0,0
res = []
while i<len(L_list) and j <len(R_list):
if L_list[i] < R_list[j]:
res.append(L_list[i])
i += 1
else:
res.append(R_list[j])
j += 1
# 两个列表中存在未合并完的数据
res += L_list[i:] if i < len(L_list) else R_list[j:]
return res
def merge_sort(lis): # 拆分
length = len(lis)
# 将列表拆分到只有一个元素为止
if length <= 1:
return lis
else:
mid = length // 2 # 按照取整,从中间分
left = merge_sort(lis[:mid])
right = merge_sort(lis[mid:])
return merge(left,right)
if __name__ == '__main__':
s = [9,8,6,7,4,3,99,5,3]
new_s = merge_sort(s)
print(new_s)
技术改变命运



 浙公网安备 33010602011771号
浙公网安备 33010602011771号