50:树中两个结点的最低公共祖先
题目:求树中两个结点的最低公共祖先,此树不是二叉树,并且没有指向父节点的指针。
树的结点定义
private static class TreeNode {
int val;
List<TreeNode> children = new LinkedList<>();
public TreeNode() {
}
public TreeNode(int val) {
this.val = val;
}
@Override
public String toString() {
return val + "";
}
}
题目解析
假设还是输入结点F和H .
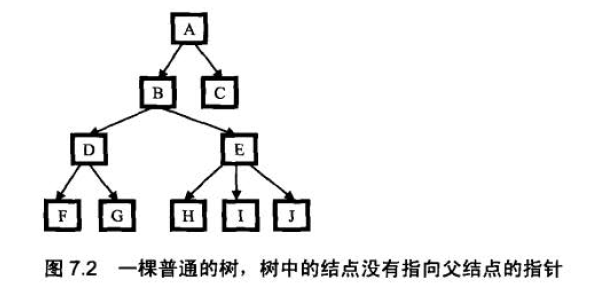
我们首先得到一条从根结点到树中某一结点的路径,这就要求在遍历的时候,有一个辅助内存来保存路径.比如我们用前序遍历的方法来得到从根结点到H 的路径的过程是这样的:( 1 )遍历到A,把A 存放到路径中去,路径中只有一个结点A; ( 2 )遍历到B,把B 存到路径中去,此时路径为A->B; ( 3 )遍历到D,把D 存放到路径中去,此,时路径为A->B->D; ( 4 ) :遍历到F,把F 存放到路径中去,此时路径为A->B->D->F;( 5) F 已经没有子结点了,因此这条路径不可能到这结点H. 把F 从路径中删除,变成A->B->D; ( 6 )遍历G. 和结点F 一样,这条路径也不能到达H. 边历完G 之后,路径仍然是A->B->D; ( 7 )由于D 的所有子结点都遍历过了,不可能到这结点H,因此D 不在从A 到H 的路径中,把D 从路径中删除,变成A->B; ( 8 )遥历E,把E 加入到路径中,此时路径变成A->B->E, ( 9 )遍历H,已经到达目标给点, A->B->E 就是从根结点开始到达H 必须经过的路径。
同样,我们也可以得到从根结点开始到达F 必须经过的路径是A->B功。接着,我们求出这两个路径的最后公共结点,也就是B. B这个结点也是F 和H 的最低公共祖先.
为了得到从根结点开始到输入的两个结点的两条路径,需要追历两次树,每边历一次的时间复杂度是O(n).得到的两条路径的长度在最差情况时是0(时,通常情况丁两条路径的长度是O(logn).
注意:可以在只遍历树一次就找到两个结点的路径,这部分留给读者自己去完成。
代码实现
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
public class Test50 {
/**
* 树的结点定义
*/
private static class TreeNode {
int val;
List<TreeNode> children = new LinkedList<>();
public TreeNode() {
}
public TreeNode(int val) {
this.val = val;
}
@Override
public String toString() {
return val + "";
}
}
/**
* 找结点的路径
*
* @param root 根结点
* @param target 目标结点
* @param path 从根结点到目标结点的路径
*/
public static void getNodePath(TreeNode root, TreeNode target, List<TreeNode> path) {
if (root == null) {
return;
}
// 添加当前结点
path.add(root);
List<TreeNode> children = root.children;
// 处理子结点
for (TreeNode node : children) {
if (node == target) {
path.add(node);
return;
} else {
getNodePath(node, target, path);
}
}
// 现场还原
path.remove(path.size() - 1);
}
/**
* 找两个路径中的最后一个共同的结点
*
* @param p1 路径1
* @param p2 路径2
* @return 共同的结点,没有返回null
*/
public static TreeNode getLastCommonNode(List<TreeNode> p1, List<TreeNode> p2) {
Iterator<TreeNode> ite1 = p1.iterator();
Iterator<TreeNode> ite2 = p2.iterator();
TreeNode last = null;
while (ite1.hasNext() && ite2.hasNext()) {
TreeNode tmp = ite1.next();
if (tmp == ite2.next()) {
last = tmp;
}
}
return last;
}
/**
* 找树中两个结点的最低公共祖先
* @param root 树的根结点
* @param p1 结点1
* @param p2 结点2
* @return 公共结点,没有返回null
*/
public static TreeNode getLastCommonParent(TreeNode root, TreeNode p1, TreeNode p2) {
if (root == null || p1 == null || p2 == null) {
return null;
}
List<TreeNode> path1 = new LinkedList<>();
getNodePath(root, p1, path1);
List<TreeNode> path2 = new LinkedList<>();
getNodePath(root, p2, path2);
return getLastCommonNode(path1, path2);
}
public static void main(String[] args) {
test01();
System.out.println("==========");
test02();
System.out.println("==========");
test03();
}
// 形状普通的树
// 1
// / \
// 2 3
// / \
// 4 5
// / \ / | \
// 6 7 8 9 10
public static void test01() {
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
TreeNode n9 = new TreeNode(9);
TreeNode n10 = new TreeNode(10);
n1.children.add(n2);
n1.children.add(n3);
n2.children.add(n4);
n4.children.add(n6);
n4.children.add(n7);
n3.children.add(n5);
n5.children.add(n8);
n5.children.add(n9);
n5.children.add(n10);
System.out.println(getLastCommonParent(n1, n6, n8));
}
// 树退化成一个链表
// 1
// /
// 2
// /
// 3
// /
// 4
// /
// 5
private static void test02() {
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
n1.children.add(n2);
n2.children.add(n3);
n3.children.add(n4);
n4.children.add(n5);
System.out.println(getLastCommonParent(n1, n4, n5));
}
// 树退化成一个链表,一个结点不在树中
// 1
// /
// 2
// /
// 3
// /
// 4
// /
// 5
private static void test03() {
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
n1.children.add(n2);
n2.children.add(n3);
n3.children.add(n4);
n4.children.add(n5);
System.out.println(getLastCommonParent(n1, n5, n6));
}
}
运行结果