最大似然估计和最大后验概率
参考链接1
一、介绍
极大似然估计和贝叶斯估计分别代表了频率派和贝叶斯派的观点。频率派认为,参数是客观存在的,只是未知而矣。因此,频率派最关心极大似然函数,只要参数求出来了,给定自变量X,Y也就固定了,极大似然估计如下所示:
D表示训练数据集,是模型参数
相反的,贝叶斯派认为参数也是随机的,和一般随机变量没有本质区别,正是因为参数不能固定,当给定一个输入x后,我们不能用一个确定的y表示输出结果,必须用一个概率的方式表达出来,所以贝叶斯学派的预测值是一个期望值,如下所示:
其中x表示输入,y表示输出,D表示训练数据集,是模型参数
该公式称为全贝叶斯预测。现在的问题是如何求(后验概率),根据贝叶斯公式我们有:
可惜的是,上面的后验概率通常是很难计算的,因为要对所有的参数进行积分,不能找到一个典型的闭合解(解析解)。在这种情况下,我们采用了一种近似的方法求后验概率,这就是最大后验概率。
最大后验概率和极大似然估计很像,只是多了一项先验分布,它体现了贝叶斯认为参数也是随机变量的观点,在实际运算中通常通过超参数给出先验分布。
从以上可以看出,一方面,极大似然估计和最大后验概率都是参数的点估计。在频率学派中,参数固定了,预测值也就固定了。最大后验概率是贝叶斯学派的一种近似手段,因为完全贝叶斯估计不一定可行。另一方面,最大后验概率可以看作是对先验和MLE的一种折衷,如果数据量足够大,最大后验概率和最大似然估计趋向于一致,如果数据为0,最大后验仅由先验决定。
二、例子
最大似然估计
最大似然估计(maximum likelihood estimation,简称MLE)很容易理解,在生活生活中其实也经常用到,看下面一个例子:
一个箱子中有白球和黑球共1000个,但是我们并不知道白球和黑球各多少个(当然这里不允许把箱子里的球倒出来逐个数),此时我们就可以用抽样的方法去估计箱子里黑白两种球的分布。假设我们抽了100次,得到的结果是70次黑球和30次白球,那么我们很自然的可以估计箱子里面有700个黑球,300个白球。你看,这是生活中我们非常自然的意识,但这其中却是用到了最大似然估计的原理哦~
在上面的例子中,我们假设总体为X,箱子里面黑球的真实概率为ppp,产生我们抽样结果(即抽到70次黑球)为事件θ\thetaθ,那么发生每次抽取后结构为有70个黑球和30个白球的情况的概率为: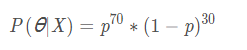
此处的P(θ∣X)就是我们说的似然函数。
最大似然估计可以理解为:选择让抽样结果发生的概率最大的参数作为总体被估计的参数。 也就是说,我们要让似然函数最大,这就很简单了,只要对上式求导即可,这时候你可能会说:对上式求导一点都不简单,哈哈哈~ 那试试先取对数再求导呢?实际上在运用最大似然估计时,一般都不是直接对似然函数求导,而是对对数似然函数求导,因为似然函数的形成其实就是一系列的条件概率相乘而得来的。
我们总结一下:
最大似然估计的终极目标:选择一个参数作为系统参数的估计值,让抽样结果发生的概率(似然概率)最大
最大似然估计步骤:
求出似然函数
对似然函数或对数似然函数求导,令方程等于0
解方程求出参数, 该参数作为总体参数的估计量
另外要注意的是,在上述抽样步骤中,正确的做法是:每抽出一个球记录颜色再放回,而不知直接在箱子里抽取100个球。因为我们需要保证:每次抽样样本颜色跟箱子里球的颜色是同分布的
最大似然估计在大数据量的情况下发挥比较好。
最大后验估计
最大后验概率估计(Maximum a posteriori estimation, 简称MAP),也是用样本估计整体,但是在使用时需要加上先验条件,最大后验估计的基础是贝叶斯公式。举一个网上的例子:
我们需要估算抛硬币正面朝上的概率,在做测试时只允许抛10次,在这10次中,恰好全部是正面朝上的,如果根据极大似然估计的思想,那么抛硬币正面朝上的概率是1,这无疑是不严谨的。因此在最大后验估计中,会设置一个先验条件,如抛硬币实验中,可设置的先验条件为P(θ)P(\theta)P(θ)服从高斯分布或beta分布。
还是以黑白球为例:
假设抽到白球的先验函数P(θ)服从μ=0.5,σ=0.1的高斯分布,则根据贝叶斯公式: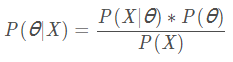
其中, P(θ∣X)就是后验概率,P(X∣θ)为似然概率, P(θ)为先验概率,)P(X)在此处与θ无关,我们可以把它理解为一个归一化常数。
那么,最大后验估计,其实就是需要找到一个θ值,使得后验概率P(θ∣X)最大。
嘻嘻 看到区别了吗:
最大似然估计,把能令似然函数最大的值作为估算值;
最大后验估计,把能令后验函数最大的值作为估算值;
仔细观察一下,在后验概率函数中,当P(X∣θ)∗P(θ)最大时,可以达到我们想要的效果。也就是说要找到一个θ值,使得似然概率和先验概率的乘积最大。 这就很像在机器学习中加入正则项来控制模型复杂度的操作,在这里先验概率可以看做是给似然概率加上了一个限制。这个过程弄清楚了之后,接下来就是求极值的问题了,这完全可以借鉴最大似然估计的做法。
下面用python的sympy库(刚发现的特别好用的一个库,求方程很方便)来对后验函数求极值。把μ=0.5,σ=0.1的高斯分布带入可得: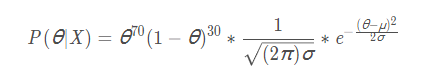
from sympy import *
def posterior(u, s, front, reverse):
theta = symbols('theta')
priorFunc = (theta**front) * ((1-theta)**reverse) ##似然函数
gaussian =( 1/(sqrt(2*pi) * s)) * E**((-(theta - u)**2)/ (2 * s**2)) ## 高斯分布
return solve(diff(priorFunc * gaussian, theta), theta) ##先求对数再求解方程
posterior(0.5, 0.1, 70, 30)
由于θ大于0小于1,解得θ=0.66,而最大似然估计时0.7,因此加入先验概率后,结果显得更“保守”一点。
总结一下:
最大后验概率估计的终极目标:选择一个参数作为系统参数的估计值,让后验概率函数最大
最大后验估计步骤:
确定参数的先验分布和似然函数
求出后验概率分布函数
对后验函数或对数后验函数求导,令方程等于0
解方程求出参数, 该参数作为总体参数的估计量
对于后验概率估计,选择合适的先验分布很重要。



