k折交叉验证(matlab和python程序实现)
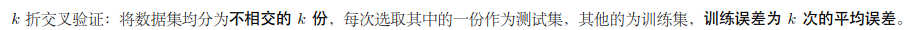
一、例子
Data = rand(9,3);%创建维度为9×3的随机矩阵样本
indices = crossvalind('Kfold', 9, 3);%将数据样本随机分割为3部分
for i = 1:3 %循环3次,分别取出第i部分作为测试样本,其余两部分作为训练样本
test = (indices == i);
train = ~test;
trainData = Data(train, :);
testData = Data(test, :);
end
程序解读:1、创建9X3的矩阵
2、把矩阵按将9行数据分成3个类
3、拿出每一类的数据拿出来进行验证
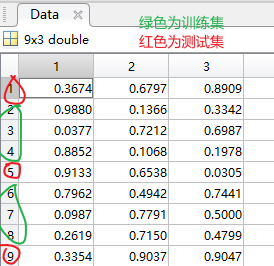
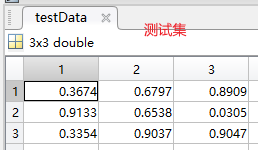
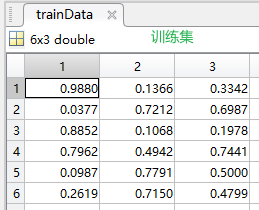
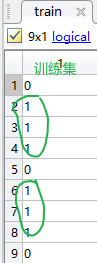
例如,最后运行的是第三类,可以看到分类中,1,5,9行为第三类数据

原始数据中的1,5,9行的数据为test_trian (检验数据),剩下的数据为测试数据。test对应的测试集数据逻辑值为1,train对应的训练集数据逻辑值为1。

二、k-重交叉验证(k-fold crossValidation):
[M,N]=size(data);//数据集为一个M*N的矩阵,其中每一行代表一个样本
indices=crossvalind('Kfold',data(1:M,N),10);//进行随机分包
fork=1:10//交叉验证k=10,10个包轮流作为测试集
test = (indices == k); //获得test集元素在数据集中对应的单元编号
train = ~test;//train集元素的编号为非test元素的编号
train_data=data(train,:);//从数据集中划分出train样本的数据
train_target=target(:,train);//获得样本集的测试目标,在本例中是实际分类情况
test_data=data(test,:);//test样本集
test_target=target(:,test);
三、利用十折交叉验证计算错误分类率
3.1代码部分
load fisheriris
indices = crossvalind('Kfold',species,10);
cp = classperf(species);
for i = 1:10
test = (indices == i); train = ~test; %分别取第1、2、...、10份为测试集,其余为训练集
class = classify(meas(test,:),meas(train,:),species(train,:));
classperf(cp,class,test);
end
cp.ErrorRate %查询错误分类率
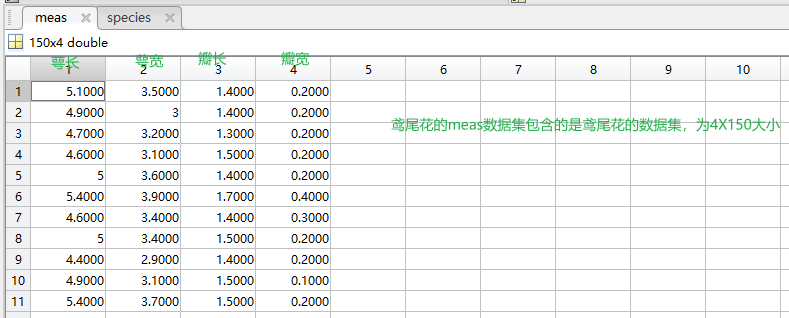
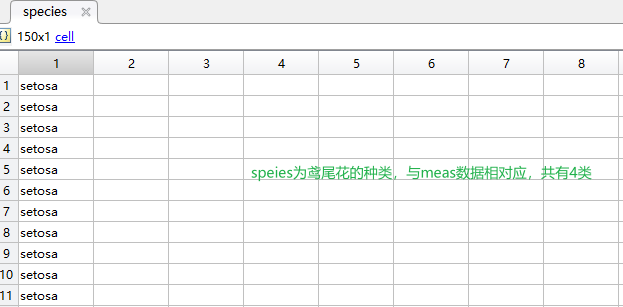
fisheriris为鸢尾花数据集:有meas和species两部分
3.2相关函数解释
3.2.1Indices = crossvalind('Kfold', N, K)
1)参数'Kfold'表明为了K折十字交叉验证,把数据集N随机分成平均的(或近似评价的)K份,Indices中为每个样本所属部分的索引(从1到K)
2)因为是随机分,因此重复调用会产生不同分法。
3)在K折十字交叉验证中,K-1份被用做训练,剩下的1份用来测试,这个过程被重复K次。
3.2.2cp = classperf(truelabels)
1)classperf是评估分类器性能(Evaluate performance of classifie)函数。
2)truelabels中为每个样本对应的真实类别,创建并初始化一个空的分类器性能对象CP。
3.2.3class = classify(sample,training,group)
1)classify是判别分析(Discriminant Analysis)函数。
2)若事先已经建立类别,则使用判别分析;若事先没有建立类别,则使用聚类分析。一般地,若已有给定的若干总体的(即若干类别)的观测资料,希望构造一个或多个判别函数,能由此函数对新的位置其所属总体的样品作出判断,从而决定其应属于哪个总体,这就是判别分析问题。
3)判别分析是利用原有的分类信息,得到判别函数(判别函数关系式,一般是与分类相关的若干个指标的线性关系式),然后利用 该函数去判断未知样品属于哪一类。因此,这是一个学习与预测的过程。常用的判别分析法有距离判别法、费歇尔判别法、贝叶斯判别法等。
4)matlab中语法:class = classify(sample,training,group) ,默认线性判别分析,将sample的每个样本进行判别,分到trainning指定的类中,返回该类表作为分类结果。还可以用参数type指定判别分析法。
3.2.4classperf(cp, classout, testidx)
1)根据分类结果,更新分类器性能对象CP。
2)在十折交叉验证法中,就是重复10次,可累积得到总的错误分类率。
四、10折交叉验证例子
第1步,将数据等分到10个桶中。
我们会将500名篮球运动员和500名非篮球运动员分到每个桶中。每个桶当中放入了100人的信息。
第2步,下列步骤重复10次。
(1)每一次迭代中留存其中一个桶。第一次迭代中留存桶1,第二次留存桶2,其余依此类推。
(2)用其他9个桶的信息训练分类器(第一次迭代中利用从桶2到桶10的信息训练分类器)。
(3)利用留存的数据来测试分类器并保存测试结果。在上例中,这些结果可能如下:
35个篮球运动员被正确分类;
29个非篮球运动员被正确分类。
第3步,对上述结果汇总。
通常情况下我们会将结果放到与下表类似的表格中:
| 分成篮球运动员 | 分成非篮球运动员 | |
| 实际为篮球运动员 | 372 | 128 |
| 实际为非篮球运动员 | 220 | 280 |
在所有500名篮球运动员中,有372人被正确分类。可能需要做的一件事是将右下角的数字也加上去,也就是说1000人当中有652(372+280)人被正确分类。因此得到的精确率为65.2%。与2折或3折交叉验证相比,基于10折交叉验证得到的结果可能更接近于分类器的真实性能。之所以这样,是因为每次采用90%而不是2折交叉验证中仅仅50%的数据来训练分类器。
五、Pyton程序
def KFoldCV(D, A, k): """ k-fold 交叉验证 参数说明: D:给定数据集 A:学习函数 k:折数 """ np.random.shuffle(D) dataset = np.split(D, k) acc_rate = 0 for i in range(k): train_set = dataset.copy() test_set = train_set.pop(i) train_set = np.vstack(train_set) A.train(train_set[:,:-1], train_set[:,-1]) # 每次的训练集 labels = A.fit(test_set[:,:-1]) # 每次的测试集 acc_rate += np.mean(labels==test_set[:,-1]) # 计算平均误差 return acc_rate/k



 浙公网安备 33010602011771号
浙公网安备 33010602011771号