梯度算法的Matlab实现

一、通过一个例子来看梯度下降法是怎么算的

函数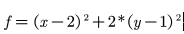,求解其最小值

　　1.求解梯度函数 

 

 

 　　2.给定初始点，计算出该点的梯度，开始迭代

　　3.计算初始点梯度模，判断是否满足终止条件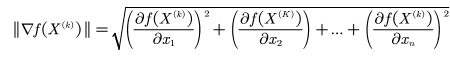，如果满足，得到终点。如果不满足，求得当前最优的学习率，然后迭代。

 

function [k ender]=steepest(f,x,e)
% 梯度下降法函数function [k ender]=steepest(f,x,e)，需要三个参数f、x和e,其中
%     f为目标函数，x为初始点,e为终止误差。输出也为两个参数，k表示迭代的次数，
%     ender表示找到的最低点。
%梯度下降法,f为目标函数（两变量x1和x2），x为初始点,如[3;4]
syms x1 x2 m; %m为学习率
d=-[diff(f,x1);diff(f,x2)];  %分别求x1和x2的偏导数，即下降的方向
flag=1;  %循环标志
k=0; %迭代次数
while(flag)
    d_temp=subs(d,x1,x(1));      %将起始点代入，求得当次下降x1梯度值
    d_temp=subs(d_temp,x2,x(2)); %将起始点代入，求得当次下降x2梯度值
    nor=norm(d_temp); %范数
    if(nor>=e)
        x_temp=x+m*d_temp;            %改变初始点x的值
        f_temp=subs(f,x1,x_temp(1));  %将改变后的x1和x2代入目标函数
        f_temp=subs(f_temp,x2,x_temp(2));
        h=diff(f_temp,m);  %对m求导，找出最佳学习率
        m_temp=solve(h);   %求方程，得到当次m
        x=x+m_temp*d_temp; %更新起始点x
        k=k+1;
    else
        flag=0;
    end
end
ender=double(x);  %终点
end

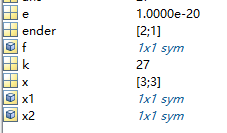
　　其中的初始点设为[3;3],误差设为10^(-20);结果为迭代27次找到了[2;1]点为最值点。

 二、学习率怎么求

　　学习率是通过损失函数求得到的。我在CSDN中看到一篇文章。有一个总结。

　　针对原始的样本（1,2）
　　针对线性回归的函数 y=kx
　　对应的损失函数是 y=2kx^2,
　　那我们的方向就是希望最小化这个损失函数，得到最终的k值，然后再代入到
　　原始的线性函数中，那具体应该如何在最小化损失函数的时候得到对应的k值呢？
　　方法一：对于损失函数求导，然后令导数等于0，得到对应的k值，有时候并不能直接解出来，并且这种方式可能是局部最优；
　　方法二：采用梯度下降与学习率的方法去求得最后的k值，明确梯度下降中的梯度
　　实际指的是损失函数的斜率，初始对于k设定一个值例如0.3，然后将k值与样本中的x值代入到损失函数中，得到损失函数的y值就是差距值，如果这个差距值符合要求就可以，但是太大的话可能就需要不断的去调节这个k值，那新的k值如何获得呢，对应的公式如下：
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　k1=k+at，
　　其中k1就是新的k值，k是初始设定的那个k值，而其中的a就是学习率，一般可以设定0.01，对于学习率的设定，如果设定的太小就会导致最终收敛太慢，而如果设定的太大的话，可能就会错过最小值点，因此需要设定合适，而其中的t就是对应算是函数的斜率，得到的方式就是对损失函数进行求导，然后将样本中的x值与初始k值代入到对应的其中得到斜率，得到新的k值，然后再将新的k值和x值代入到损失函数中，看下函数的差值是否在那个区间内。
　　总结：梯度下降其实就是斜率不断的下降，最终希望是斜率为0对应的就是在谷底的时候得到对应的k值，就是最好的k值。