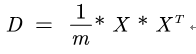协方差矩阵

统计学的基本概念（原文链接）

一、

　　有n个样本的集合: X = {X1，X2，...,Xn}

　　均值：

 

 

　　 标准差：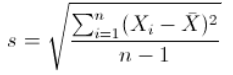

 

 

 　　方差：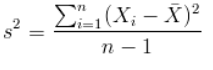

 

 

 　　　　有两个数据集,数据集1，X = [0,8,12,20];数据集2，Y = [8,9,11,12]。两者的均值一样都为10。数据集1的标准差8.3，数据集2的标准差为1.8，因为后者的数据分布比较集中，标准差描述的是这种散布度。之所以除以n-1而不是n，是因为这样使我们以较小的样本集更好的逼近总体的标准差，即统计上的无偏估计。方差是标准差的平方。

二、为什么需要协方差

1、

　　标准差和方差一般是用来描述一维数据的，但现实生活中遇到的通常是含有多维数据的数据集，最简单的是大家上学时要统计多个学科的考试成绩。另外，我们想要知道两件事之间的关联程度，例如，一个男孩子的猥琐成都和他受女孩子欢迎程度是否存在联系。协方差就是解决这样一个问题，度量两个随机变量关系的统计量。

　　仿照方差的定义，度量各个维度偏离其均值的程度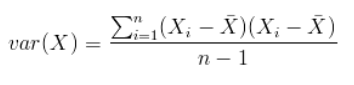

 

 

　　协方差定义为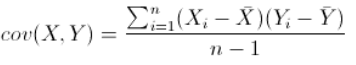

 

 

　　协方差结果的意义？如果结果为正值，说明两者是正相关，也就是说：一个人越猥琐越受女孩子欢迎。如果结果为负值，说明两者是负相关，说明女孩喜欢正经的人（不太可能）。如果为0，说明两者没有关系，相互独立。

 

2、

 

　　上述是两件事的关联程度，如果是三件事{X,Y,Z}就需要用矩阵表示了，这就是协方差矩阵。

 

 

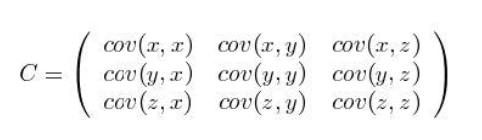
3、协方差的计算

　　3.1

　　　　两个数据集A和B的组成的矩阵X为

 

　　 　　　其协方差矩阵正好与矩阵(X*X的转置)/m相等，如图所示

　

 

  　　 3.2

　　　　　　如果是三个数据集A、B、C组成的矩阵Y为

 

　　　　　　 同理验证

 

　　3.3 

　　　　同理可以推广到更高维空间，所以可以直接使用数据集组成的矩阵计算协方差矩阵，即