对【XGBoost】的理解
【零、背景简介】
XGBoost 于2016年由陈天奇提出，一种用于可扩展的分布式的大规模机器学习算法，在Kaggle多项比赛中高频获奖。
核心思想是基于残差的树Boosting，它在建树计算split点、泰勒2阶展开计算损失、正则处理、特殊值处理（如空值处理）、列采样、系统并行化等方面做足了功夫，自提出后威震学术界和工业界！至今依然广泛运用。
本文记录并总结学习该文时的个人理解， 若有理解错误 ，还望大佬指正。
论文简述的4处特点：
1、一种高度可伸缩的基于端到端的提升树算法。
2、一种分布式加权直方图调整框架，以进行高效预计算。
3、一种自适应稀疏处理的并行树学习算法。
4、提出了一个有效的缓存块结构，以支持外存计算。
【一、基本概念 及 目标函数】
1.1 基本概念
设 D = （Xi, yi) 为数据集，样本数为n , 特征数为m, F表示多个分类回归树CART，T表示一棵树的叶节点个数，q表示树结构（当树建立好后，q(Xi)表示对Xi样本判定的叶节点，w表示叶节点权重，Ij = {i | q(Xi) = j} 表示第i个样本被当前树划分到第j个叶节点上。
式（1）表示对样本Xi 的计算过程，有基于Boosting的串行集成学习思想。模型对Xi 的预测值yi_hat是经多棵树预测后对每棵树预测结果累加后得到的（分类情况则使用分类类别最多的类别，或对yi_hat进行Logistic或softmax函数计算后得到的样本类别。
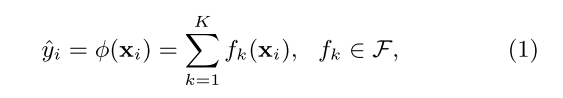
1.2 目标函数
目标函数组成由损失函数 + 正则， 正则项由叶节点权重w的二范数构成，
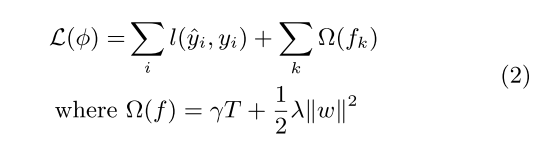
损失函数巧用泰勒二阶展开式，将上一时间yt-1_hat作为变量x, 当前时间 ft(Xi) 作为增量 Delta_x
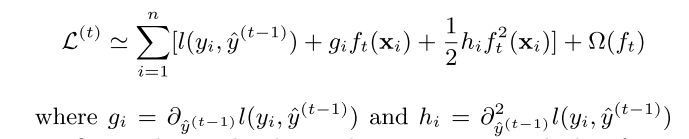
gi、hi 分别是对目标函数对yt-1_hat的一阶和二阶导数，最终目标函数如式3：
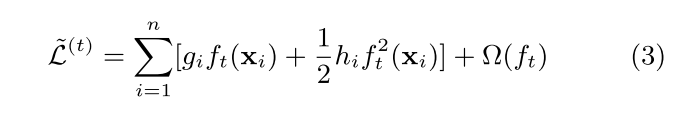
建模时，对X中每一个样本进行计算，并对相同叶节点下不同计算的样本进行权重w合并（如式4）
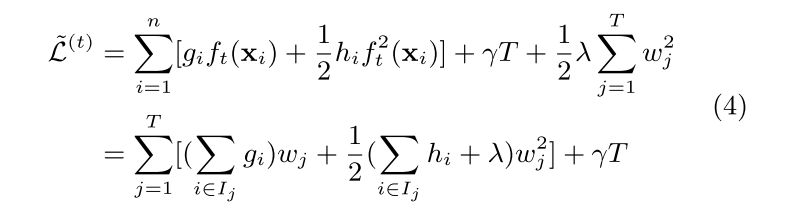
计算目标函数的最小值时对应的wj* 和 L(t)(q) ，可直接计算 dL|dwj 导数并另其等于0， 求出wj* 并带入求出 L(t)(q)
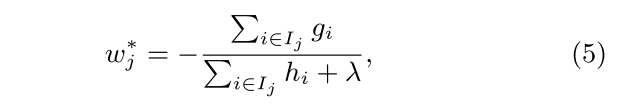
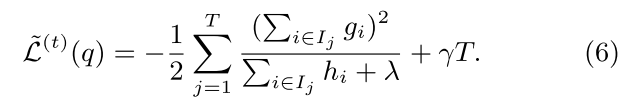
注意在Boosting计算每棵树时，可以使用收缩率Shrinkage，
【二、节点split策略】
2种方法：精确贪心算法 和 split近似算法。
定义增益gain ：表示对已选择属性k对第j处属性进行split后增益变化值量化，该值越大表示越此处越适合split
在筛选属性列时，可以适用所有列m， 也可以进行列采样（column subsampling) , 列采样可以全局随机选取若干列，在计算split时依次使用， 也可以在每创建一层的split时，再进行列采样，
使用列采样可以降低过拟合（因为增加了随机因素），同时在建树时可以充分并行化
2.1精确贪心算法
当数据量不是非常大且算力够用时，该算法能保质建树时，所选属性的最优属性值的split点
2.2 近似算法
在分布式或算力缺乏时，可以适用近似算法来寻找该属性列的最佳split点，通过对属性的分桶，计算不同桶间的gain，并得到最优解
【三、算法其他处理】
3.1稀疏数据的处理
实际问题中，会出现稀疏数据的情况。如：1）缺失值；2）数据中本身出现很多0；3）使用one-hot编码增加稀疏性，所以对稀疏数据的处理很重要。
原文中，增加对每个节点默认的方向，当数据中存在缺失值的时候，就会统一把缺失数据样本分到左子树或统一分到右子树，
【四、系统优化处理】
4.1 Column Block
在大数据量情况下，耗时的操作是对数据排序（尤其在计算split时反复排序），同时从磁盘读取数据非常耗时，因此原文将数据已block块的方式存储在内存中。类似于列存储，且在内存中对各列列值进行一次排序，并保留排序结果，使在训练模型时可以反复利用。
4.2 Block size优化
优化Block size 为提高Cache命中率：（1.当Block size过大时，预读取到cache可能放不下，要多次读取磁盘，较费时； 2. 当Block size过小时，预读取到cache导致整体命中率偏低，没有充分发挥cache高速缓存功能，提速不明显 ）
4.3 对Block并行放入多个磁盘中
对Block进行压缩并放入多个磁盘中，使得预读取数据时，在磁盘处可以并行减少读取数据时间。 （计算机中各部件速度不等式 ： CPU > cache > 内存 > 磁盘 ）
【五、总结】
1. xgboost 高准确性，可缩放（支持分布式) ，高度并行化， 底层优化做的很扎实，在各种比赛和实际工业界中很受用。
2.对于空值和稀疏数据的考虑，使得在实际应用中适用场景极多。
3.多种操作Shrinkage 列采样 正则 有效降低过拟合
4.在精确性和计算效率上做了多种实现，适用多种场景，使用者可以自己根据实际情况trade off.
5.在适用泰勒二阶梯度展开来计算权重
