流体的物理性质和描述流体运动的物理量
连续介质假设：部分内容省略，详见教材。
在研究流体时，我们取微团进行统计平均来取各个物理量。
例如密度，我们在取微团时，微团的尺度在微观上要充分大，宏观上充分小。因为微观上如果仅包含个别分子，则统计结果波动太大，宏观上如果太大，则无法描述局部的性质。
流体的密度会随温度以及压力的变化而变化，随温度变化时称为热膨胀性，随压力变化时称可压缩性。
对于有相对运动的两层气体（注意是气体不是液体）来说，界面上因为分子热运动导致的动量交换（高速和低速粒子穿过界面进入另一个速度的流体中），导致形成粘性，可以大概理解为滑动摩擦力。
对于有相对运动的两层液体来说，一般认为粘性来源于，界面上的分子引力，阻碍相对运动。
切应力与速度梯度有关系，所以如果是线性切应力，我们直接用U比h，因为真个切面上的速度梯度是一样的。更一般的就要取u和h的微元来算速度梯度。
系数μ是和流体本身的性质有关的。
注意，温度升高气体粘性增大，液体相反。因为温度升高分子热运动加剧，而液体引力降低。有一个典型例子：冬天温度低时倒食用油更困难。
不遵循以上规律的称为非牛顿流体，本课程内只研究牛顿流体，即粘性与速度梯度呈线性关系。
中间有一段没有PPT
有了运动方程便可以求解初始质点运动后的位置，通过一次求导可求速度，二次求导可求加速度。注意abc表示初始位置（用来标记质点），t表示时间。
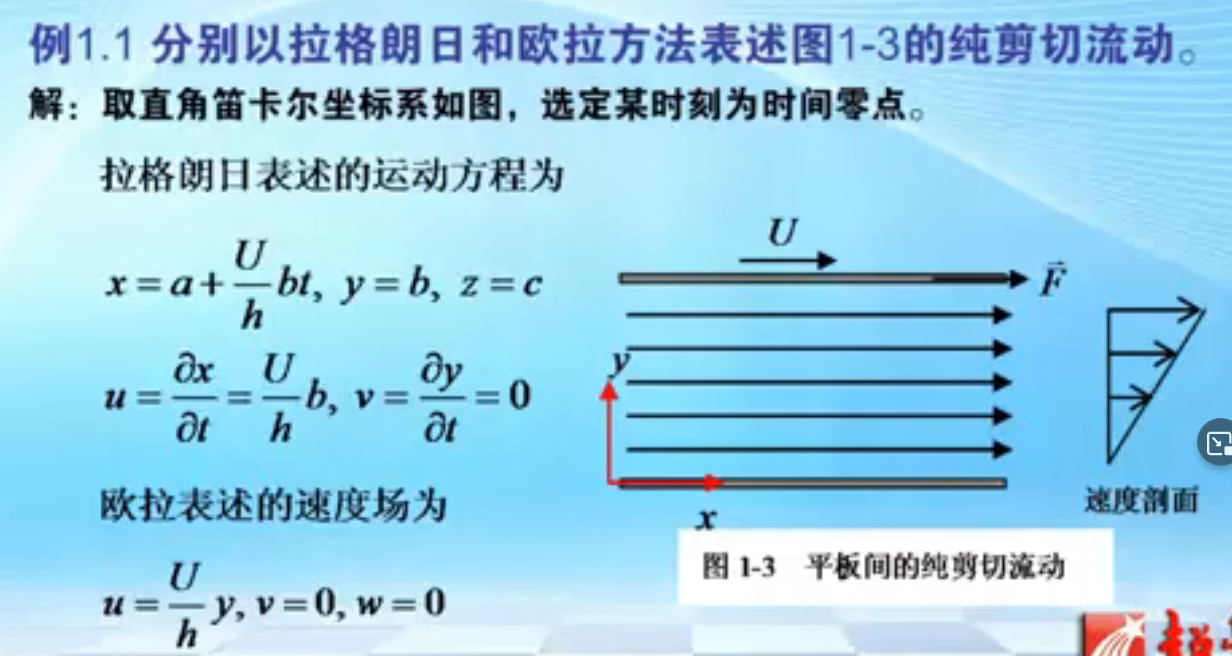
欧拉方法是通过速度场描述运动的，如何写出加速度：
上式中，填了一项再把它减去，前面已经用过好几次这个方法了。这样就可以使原式可计算可解释。
现在式中第一项是同一位置速度的变化，第二项是同一时间内不同位置的速度的变化量。
可见，在欧拉表示下，速度和加速度的关系不是单纯速度对时间的导数了，还多了一项。
上式只是x分量，下面还有其他两个分量。
三个分量合并后，可以写成矢量的形式。其中第一项我们叫局地导数，第二项我们叫位变导数，这两个合起来称为全导数（随体导数）。
最后一行，如果将V提到外面去（第一行的分量形式也是一样可以提出去），就剩下式中的东西，又记为D/Dt，又称全导数。
对于一个东西求全导数意味着对他求局地导数和位变导数。
所以欧拉表述下，速度的全导数才对应加速度。注意，这个加速度仍然是定义在某一个具体运动的质点（流体微团）上的，是在欧拉方法下对质点的某个物理量变化率的表述方法。（要跟着这个微团走的，所以全导数又叫随体导数）
我们的研究工具研究方法，例如牛顿第二定律都是对于物体而言，而非对于空间（场）而言，所以必须要有随体导数。
1）全导数为0代表流体微团的加速度为0，说明该场中所有流体微团都是匀速直线运动
2）局地导数为0，表示该场是定常的，任意点的速度不随时间变化。
3）三个速度分量的梯度为0，梯度描述场的不均匀性，所以这一项表示速度场是均匀的。
4) 位变导数是0表示在任意点处，沿着速度方向，速度的变化率是0。
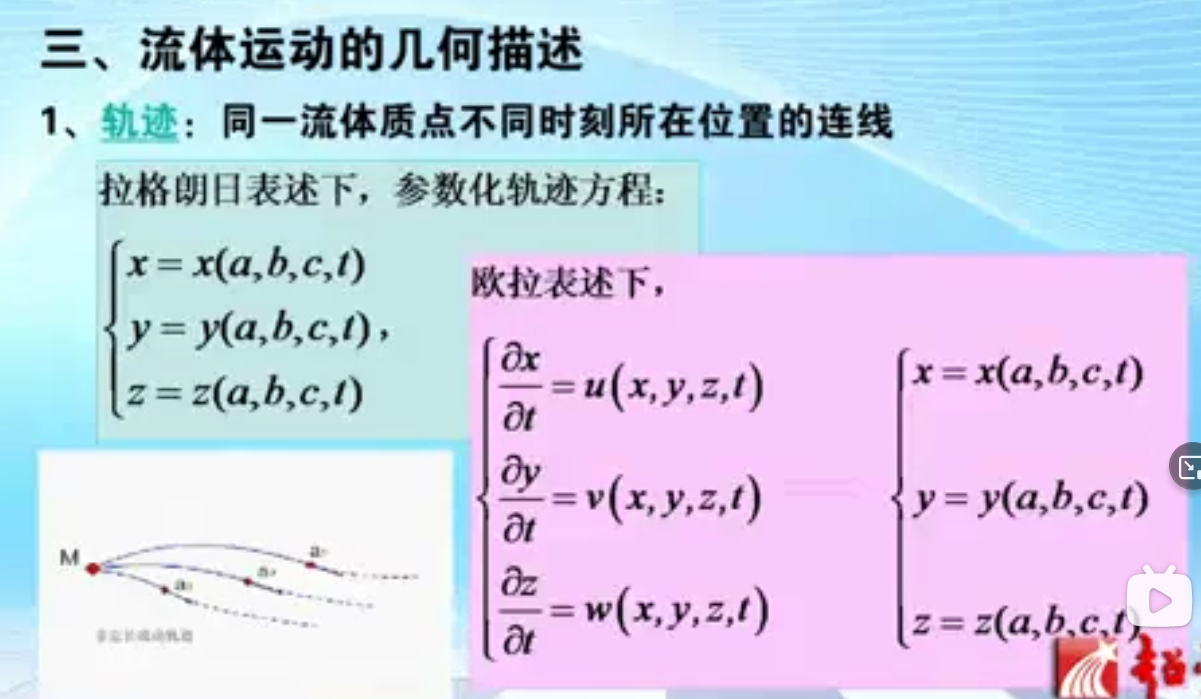
我们知道拉格朗日是追踪法，所以质点的轨迹是好求的。欧拉需要转化到拉格朗日
粉色的部分就是欧拉如何对应到拉格朗日三个速度分量的表示
流线上切线方向的三个分量与速度的三个分量对应成比例。所以流线的方向即瞬时速度的方向。
如果速度的方向是定常的，流线就与轨迹重合。速度大小不影响，流线只能表达出方向并不能表达出速度大小，刚也说了成比例即可
流线是流场的瞬时状态的描述，轨迹则是针对具体质点（微团）的
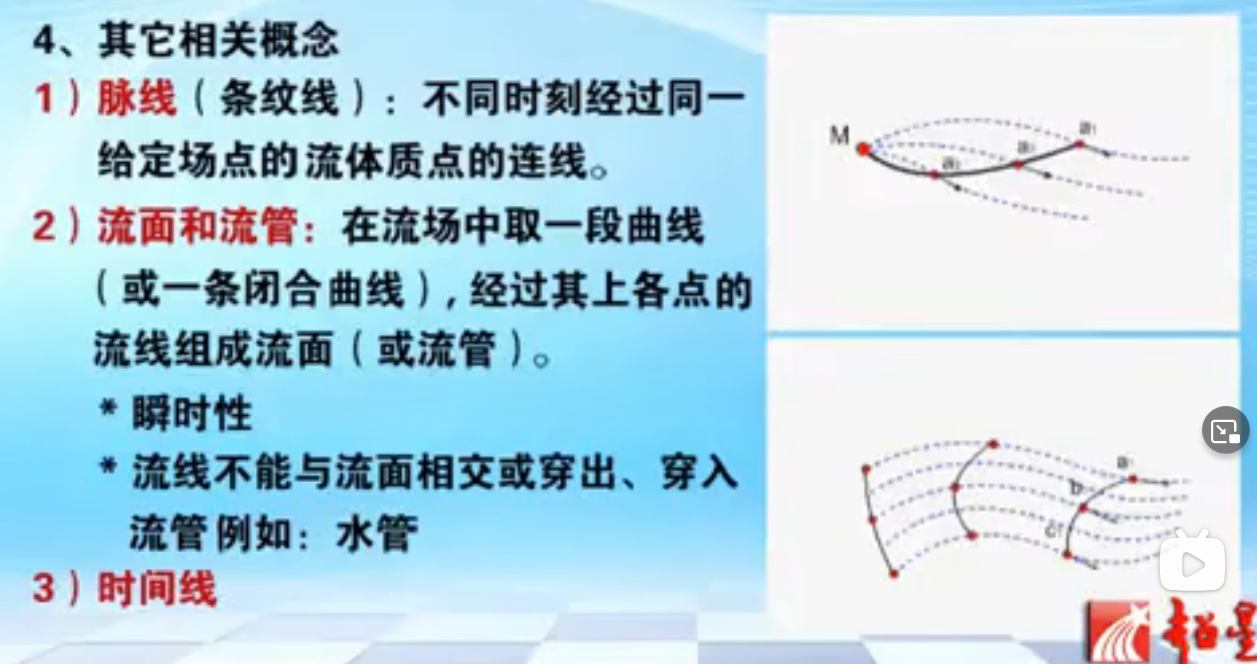
右面上图是脉线，下图是时间线。
流面是先取一段线，然后该线的运动轨迹组成一个面。这个面上的切线都是速度方向，所以不会有流体穿过这个面。
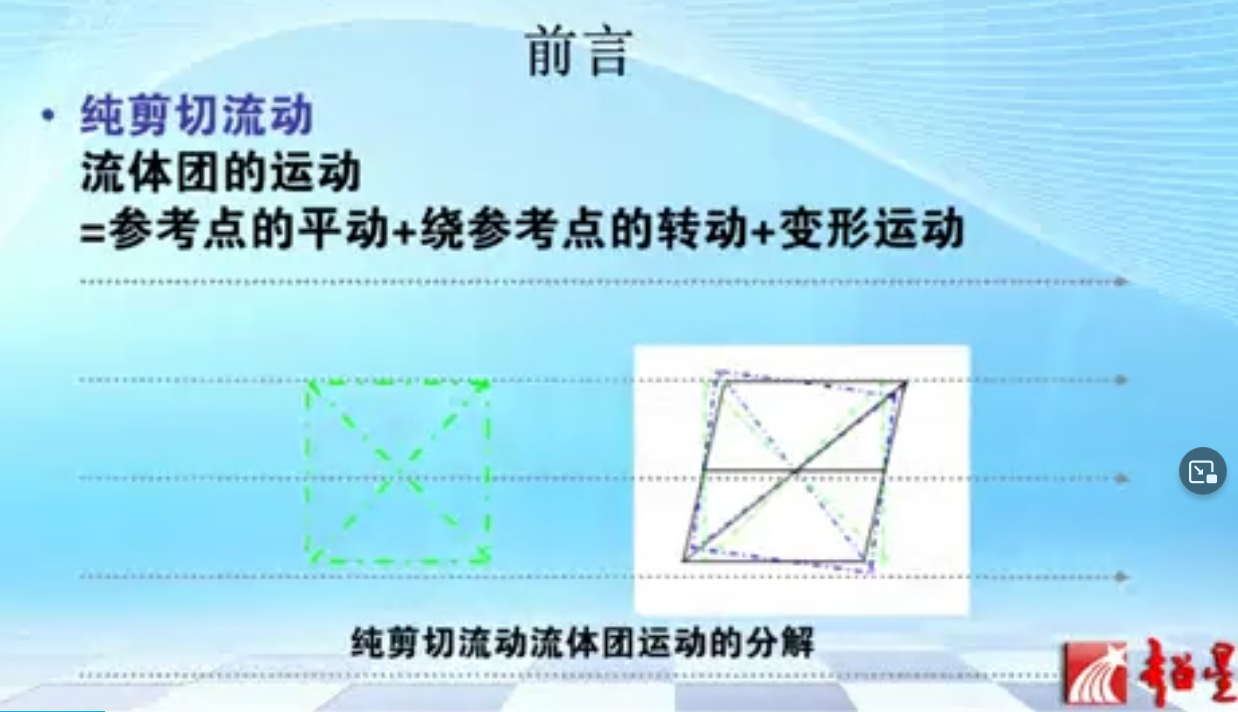
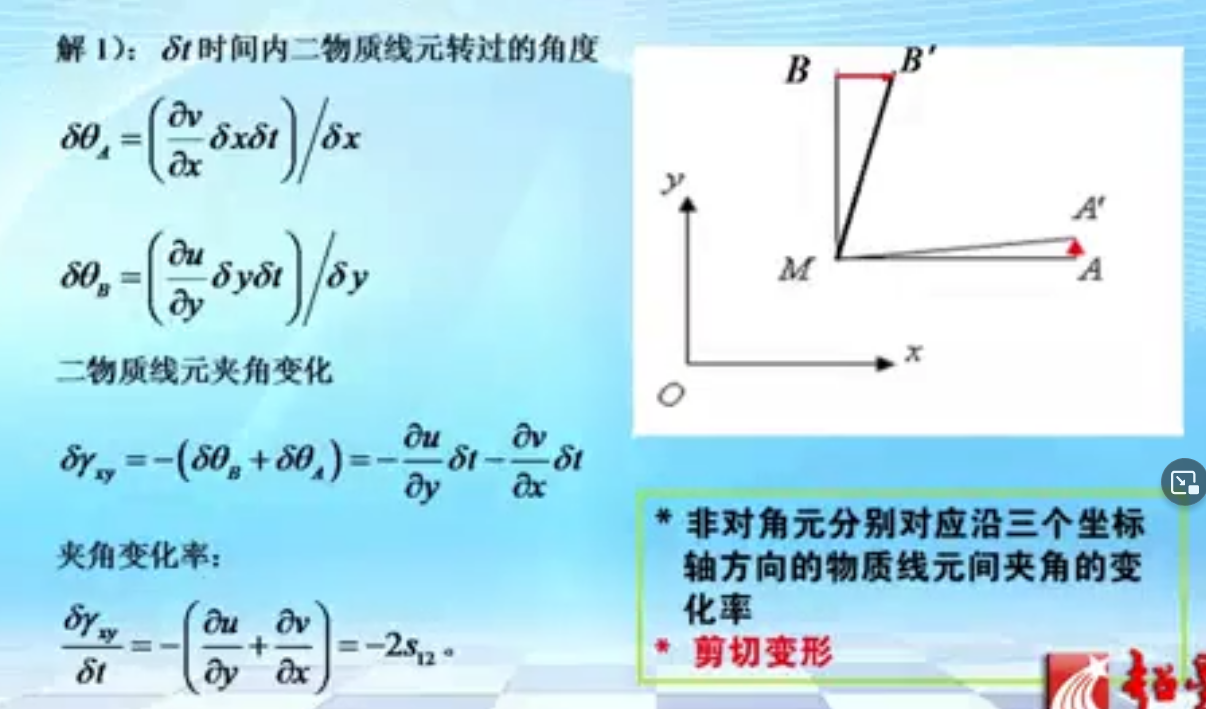
我们现在探究相对于M'点相对于M点的相对速度大小，注意是相对速度
粉色框上式是相对速度的三个分量，每个速度分量又在三个方向上有三个分量。把上式表达成矩阵运算则如下图所示
其中，我们把中间的大矩阵记为E，再拆成1/2组成一个新的式子，Ec是其转置
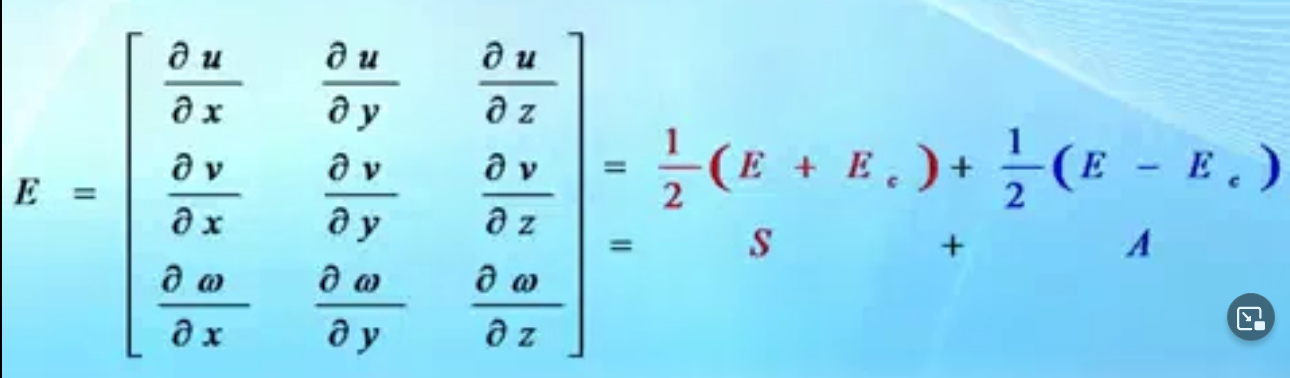
注意，分开后一部分记为S，一部分记为S
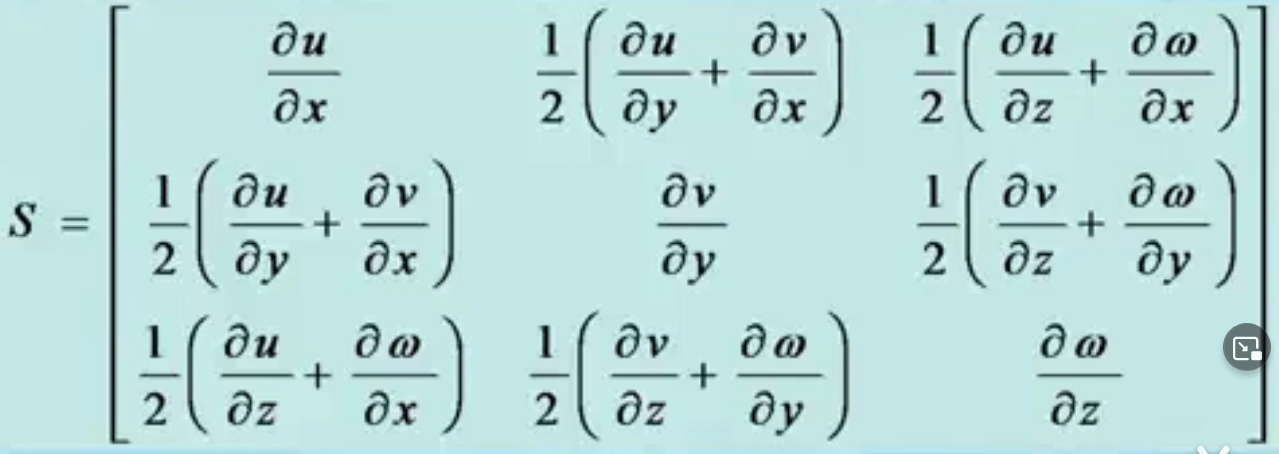
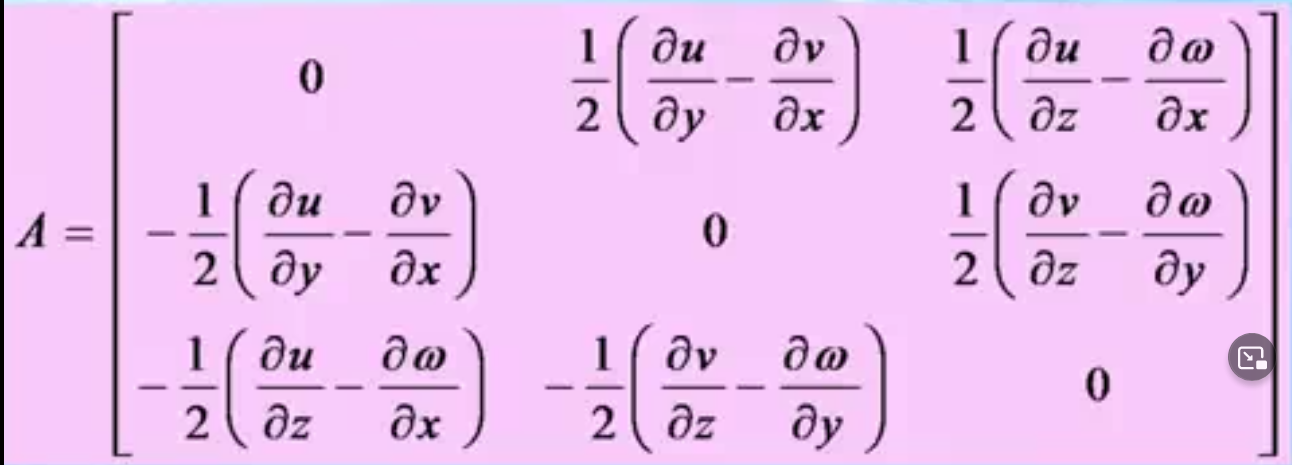
对应的，相对速度的表示也就分解为两部分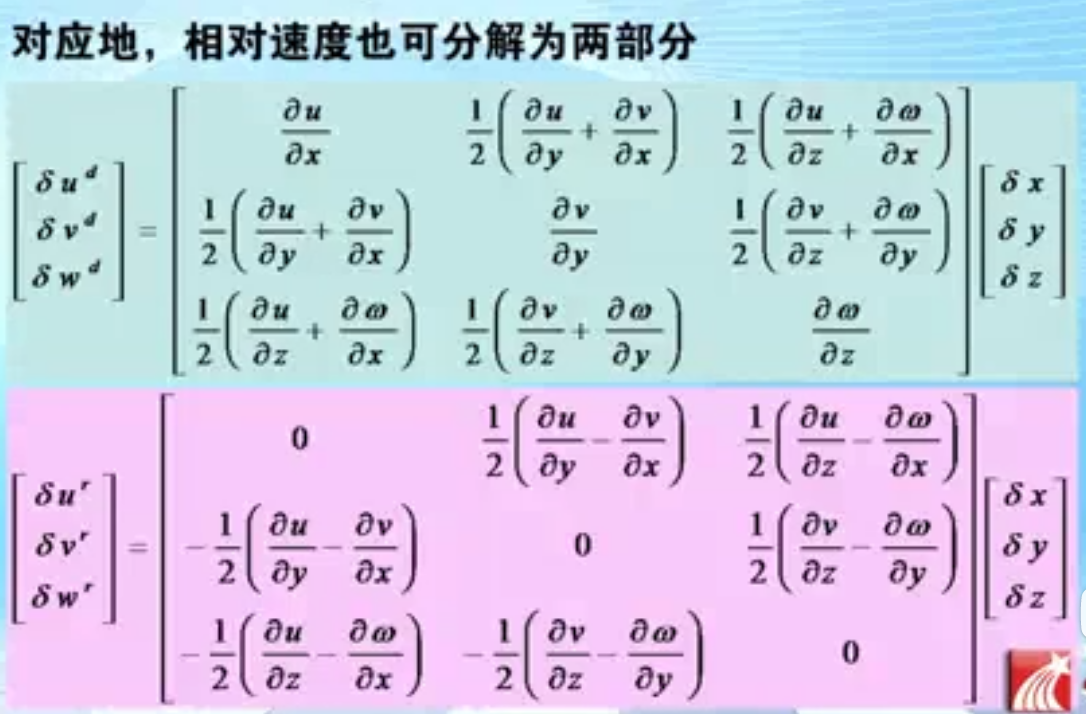
第一部分的上角标是d（注意绿色框里的是一个对称矩阵），第二部分上角标是r（注意粉色框里的是一个反对称矩阵）
我们先看粉色框的反对称矩阵代表什么。首先看黄色框，我们把速度场的旋度乘以1/2，将这个式子记为ω，然后就会发现矩阵中的元素就是ω的分量或者其相反数。这样我们就可以如下面绿色框，把相对速度的这一部分（一共两部分）记为ω和δr的叉积。——流体微团的刚性旋转
第二部分是变形运动，但老实说不需要深究机理。
粉色框：由于上面我们探究的是M'相对于M的速度，所以M'的速度实际等于M的速度加上它们的相对速度
三个对角元之和刚好是速度散度，它表示单位时间内流出流体的体积。
为什么单独提出对角元之和讨论：矩阵中的元素的形式随选取不同的坐标系变化，但三者之和——速度散度不变，它是一个物理事实。
P代表静压强，I是单位矩阵，负号表示与y方向相反。
