场论

就像我们之前学过的静电场，所谓场就是在连续空间内连续存在的，而不是个别几何点

那么场强E就作为位置r的函数，其存在于空间D中

我们考虑一个空间内空气的流动，就会有一个流场。

对应的还会有该场上各个物理量的场，例如密度场、温度场、速度场等等，他们都是空间D中位置r的函数。这些物理量分为标量和矢量。

如果某个物理量的场是随时间变化的（刚才说到的是静止的情况），那么该物理量除了位置r以外，同时也是时间t的函数。

我们将不随时间变化的物理量称为定常，其场称为定常场。变化的就是非定常（场）。

 

梯度：空间不均匀性。首先引出方向导数（即偏导），以密度场为例

 

 可见，任意方向上的微元δs的方向导数，都和一个矢量有关，我们把这个矢量定义成梯度gradρ

δs的方向导数=梯度在s方向上的投影，如果该矢量与s方向同向时取得最大值。可见这个矢量的物理意义是该点上的所有方向中，这个矢量的方向的方向导数是最大的。从几何上也可以解释这个观点，三个方向上的偏导数合力方向就是增长率最大的方向。

以上我们用密度（标量）举例，其梯度含有三个分量。像速度这样的物理量，本身就有三个分量，这三个分量本身都有梯度，其中包含三个分量，所以描述速度的空间不均匀性需要九个分量。

 

 梯度的运算法则其实就是导数的运算法则，尤其注意乘除运算。

 

两个定理：对于任意一个标量场Φ来说，

（2）如果有一个保守力，其力势的梯度就是这个力。反过来如果能找到一个单值函数（方向的函数），其梯度总是能对应一个矢量，那这个矢量的环路积分一定是0，也就是说这个力是保守的。例如对于一个速度场，如果速度的环路积分是0，那么它的速度一定可以用某个标量函数的梯度来表示，就可以引入一个速度势，从数学上讲，与重力势，电势是一样的。

对于1，注意δr是一个标量，一个长度，r^是一个方向，他俩乘起来就是r（向量）

对于2， 保守力做功与路径无关，我们就可以引入势，例如重力等。保守力和力势之间的关系就是梯度关系（从物理意义上容易理解，重力势的梯度当然是重力）。引入势以后，我们可以忽略复杂的中间过程（环路积分为0），使得求解的过程变得非常的简单。

 

 

 

 

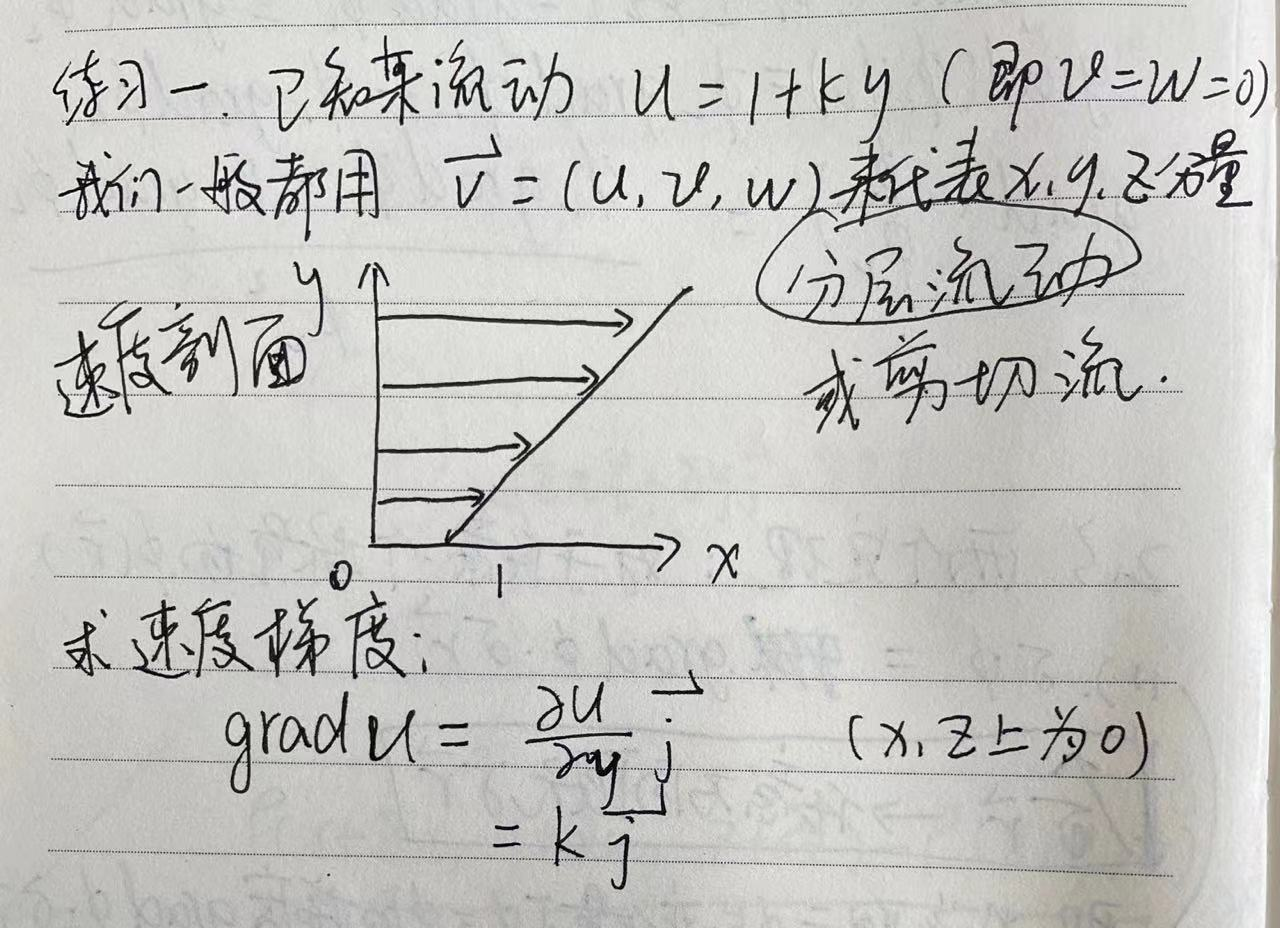
 通量：（例如质量通量）单位时间内经过某横截面的流体的质量

假设均匀速度流穿过其法相的一个横截面，流速为u，流体密度为ρ，横截面面积为s，我们取一个小时间段δt研究

那么这一段时间内穿过横截面的体积就是长（uδt）*横截面面积，再乘上ρ变成质量，除以δt取单位时间，最后就是ρus

如果横截面的法向不沿着速度方向而是有一定夹角，则取横截面在速度方向上的投影（该投影法向沿流体速度方向）。

当考虑不均匀流，横截面是曲面的时候，我们采用微积分的思想，取极小面积，近似认为是均匀流流过一个平的横截面。注意，真实流体可能有各种方向的流，此时我们需要确定一个正向，最后算出该曲面上的净通量。

更常用的，我们会取一个闭合曲面，此时一般取闭合曲面向外为正方向。

 

注意，通量是一个积分量，它不仅取决于横截面的位置，还取决于横截面的大小和形状。

我们现在定义散度：

 上式分子上是通量，下面除以体积，表示单位体积，描述的是在这一点附近这个物理量的变化率。散度是一个微分量，它描述的是一个点附近的某种性质，它不受认为选取的截面的大小和形状的影响。它只与场点位置有关。

假设有一个小水团受热膨胀，取一个闭合曲面包住这个小水团，我们再用散度定义的公式去计算，那么散度的物理意义就是单位体积空间单位时间内向外扩散了多少质量，这是“散度”的直观理解。当散度=0，我们称为无源，当散度≠0，我们称为有源。

奥高公式：

 

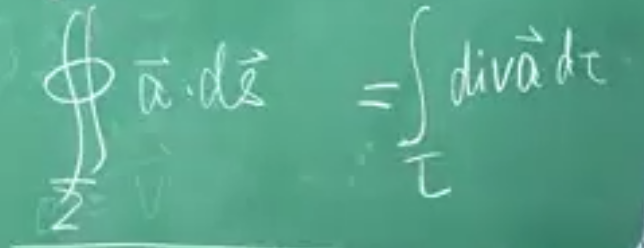
 作用：1. 把面积分转化成体积分，把计算通量转化成计算散度（数学）

2. 公式右边是矢量场a在体上的积分，取决于所有a的性质，左边只取决于a在该体表面的分布（物理）

 

 与通量一样，我们先介绍一个积分量，速度环量：速度在闭合回路上的积分，通常用Γ来表示

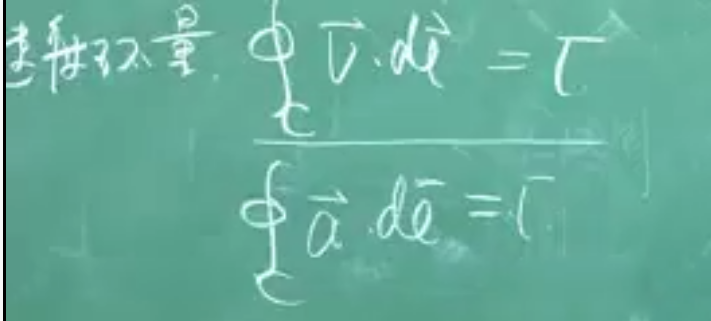
 容易想到，速度环量虽然能够描述旋转运动，但它还与你积分的那个环路的大小有关，即不同环路大小上的速度环量不同，但有可能角速度相同。从数学上讲，我们更喜欢能够纯粹描述一种性质的微分量，所以进一步引出旋度。

 旋度的物理意义参照梯度理解，梯度是所有方向导数中最大的那一个，任意方向的方向导数都是该方向在梯度上的投影，方向与梯度同向时取得最大值。旋度相同，旋度是矢量场在以旋度方向为法向的平面上取得最大旋度，任意其他方向的平面旋度都是投影。

旋度本身也是一个矢量，需要用三个分量来表示，它们的计算公式为：

 

 

 

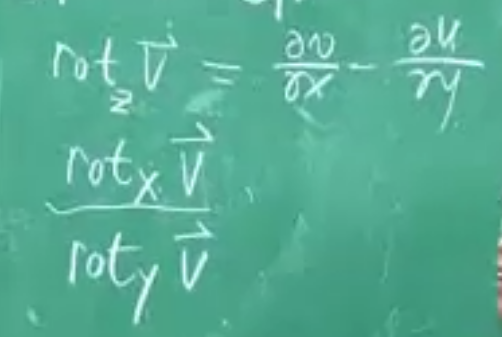
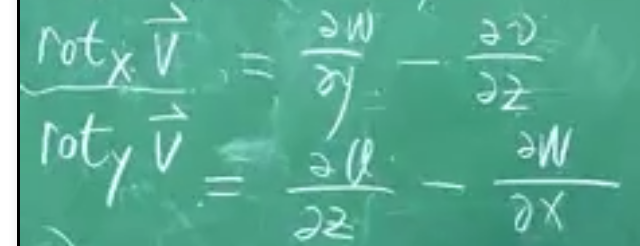
 记忆方法：z分量就是xy平面上的，所以和xy/uv有关系，然后xyz/uvw是顺时针旋转的，前面是正后面是负。

 上面写的是三个分量，算旋度需要把三个分别乘以ijk然后加起来。

 

斯托克斯公式：

 

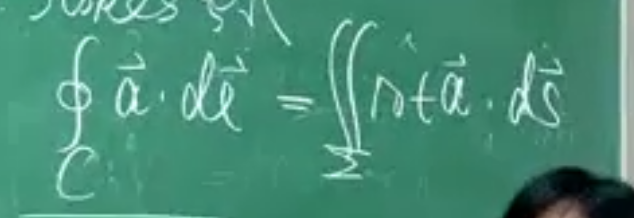
 C为矢量场中的闭合回路

该公式表示向量a在C上的环路积分可以换成以C为边界的面Σ上a的旋度的面积分。

但要注意，斯托克斯公式的用处主要不是用来做积分变换的（线积分变成面积分），它主要用于表示涡旋运动中涡通量（公式右）与速度环量（公式左）具有相同的地位和作用，遵循着相同的动力学方程。

 

如果一个物理量例如速度场V的旋度处处为0，我们称为无旋流动，否则是有旋流动。

根据斯托克斯公式，无旋流动的空间中任意曲线C的速度环量为0，保守力做功为0，可以引入保守力势

 

哈密顿算符：

 

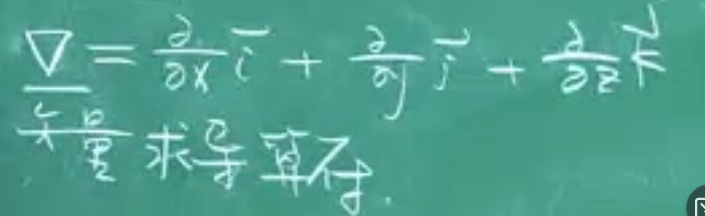
 例如梯度的公式就可以用哈密顿算符表示：

 

 

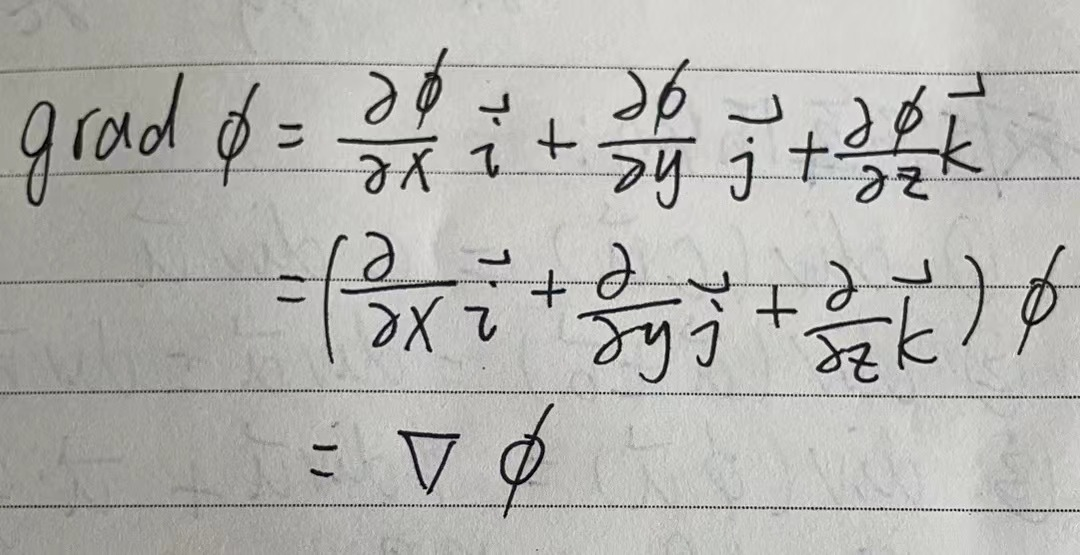
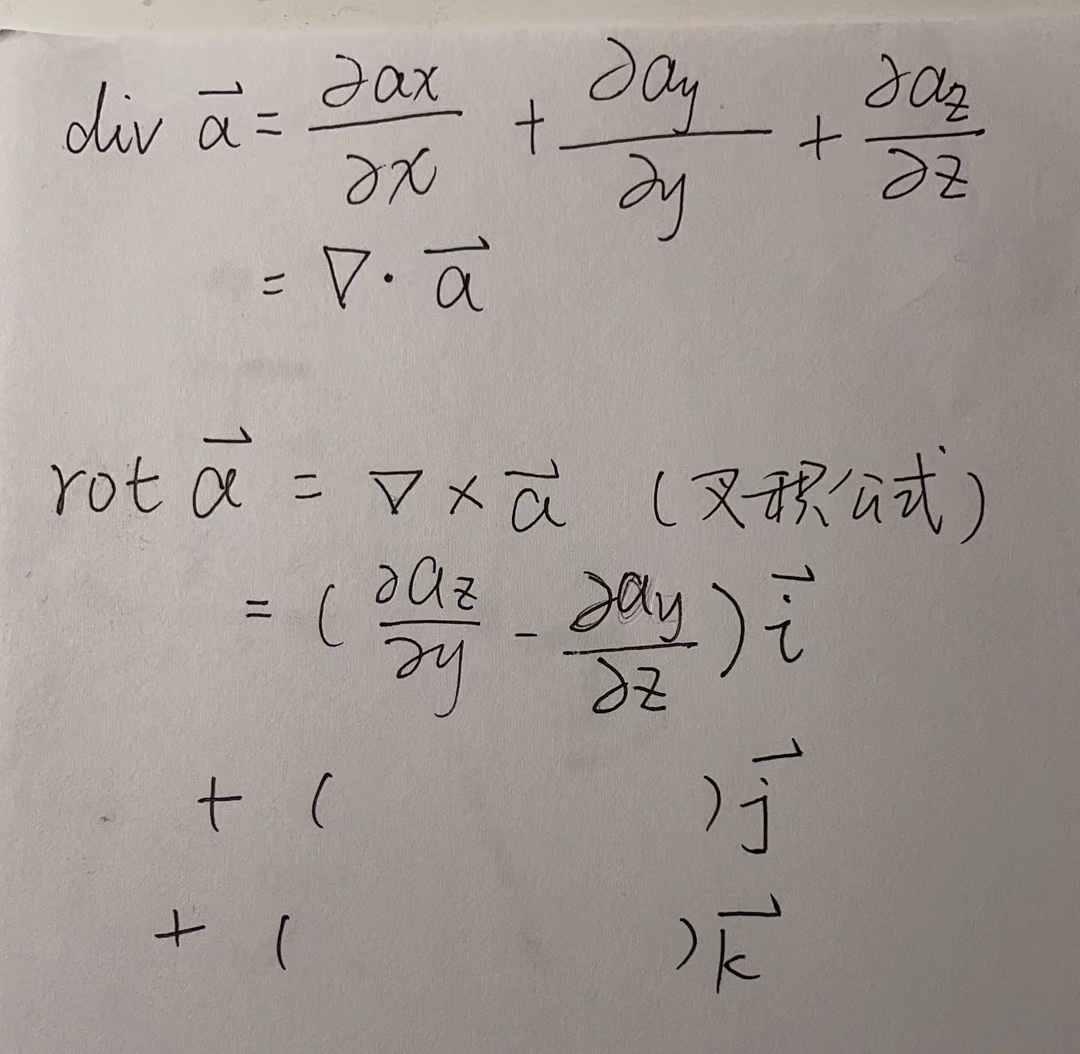
 注意，将梯度、散度和旋度用哈密顿算符表示时，将哈密顿算符完整的写为上面给出的哈密顿算符的公式，然后该进行什么运算就进行什么运算。

哈密顿算符公式里的那个东西时不完整的，和向量运算后，就是一个完整的公式了，偏导就有了作用对象。

总结一下：

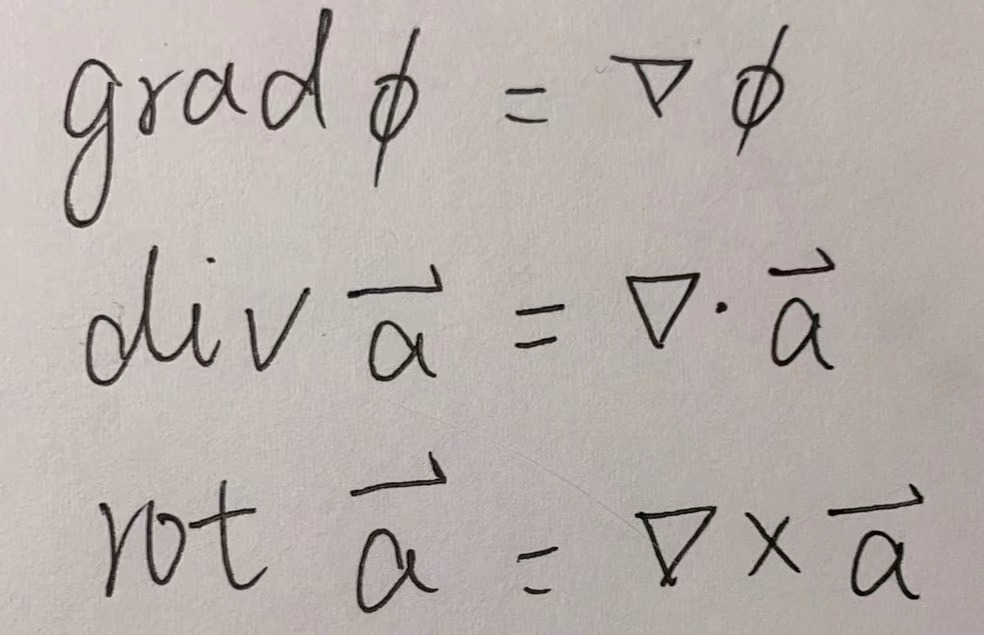
最后，两个哈密顿算符点积，再作用在一个物理量（矢量或标量）上，即拉普拉斯算符

 

 

 

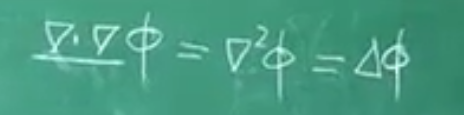
 后面还要遇到用哈密顿算符给各种复合的场做运算，熟练了以后并不需要完全展开算，记住以上规则就可以直接写。具体操作方法在P8，老师演示了一次，P9中有一个复杂的例子