大洋环流与水团

这里面广阔、长期都是模糊的说法,具体多广多长跟你关注的问题有关系。


风生流即风吹的流,密度梯度则会导致压力不均匀形成压力差。

表层流比较剧烈,越往下相对来说流速要更弱。
我们所说的大洋环流基本上是表层的流,深层的东西我们知之甚少(观测困难)。

风生流:风海流、漂流
密度流:热盐环流

注意以上分类是不同角度的分类。

追踪法:跟着某一个海流走,用的少。
定点发:谁来测谁,用的多。因为一般仪器是固定的,也有随着海流走的仪器,容易丢失。

注意海流方向与风向定义相反。

密度与温度、盐度、压力直接联系(由三者算得),盐度在大洋种变化极小,而海水我们通常又假设它是不可压缩的(如此假设可以极大简化问题),所以我们通常认为温度的变化引起密度变化,进而决定海流。
与我们之前讨论过的大气高压低压区域一样,如果只关注温度分布,海水应该自然的逐渐趋于温度相同,但高压低压、高温低温区域都是稳定存在的,就是因为气体/海水是流动的,维持了这些区域的稳定存在。
在此,老师再次强调不要形成思维定式,不要先入为主,过于执着。很多例子都是某人已经发现一个东西,但由于和信念中的东西不同,所以它认为是数据、仪器或者方法出错了,实际这正是他寻找的东西,直到被别人提出来以后才能恍然大悟。
海流的形成:



风应力对应风生流、风海流、漂流
压强梯度力对应密度流、热盐环流
压强梯度力由不同海域的密度梯度造成,但是此处有个矛盾点,之前说密度受压力影响,并假设了海水是不可压缩的。这里又说因为密度梯度形成了压力梯度造成海水受力形成海流。
更正:这里不矛盾,确实是不可压缩的,但温盐变化造成密度变化,形成压强梯度力。我们在讲密度的部分就认为海水不可压缩,且盐度变化不大,所以主要受温度影响。
除了图中说到的三种力以外,海水还受引潮力,但因为和大洋环流关系不大,一般在环流这里不予考虑。

质量守恒:固体运动中,整个物体质量同时运动一般不太考虑。但是液体需要注意质量守恒。当一处海水流走了以后,一定要有其他地方的海水流进来,一处动处处都得动,是一个连续的过程,所以称为连续方程。
边界条件:海岸或者研究区域的边界的条件;初始条件:一开始的时候海洋的状况,这个里面包含大量的假定,因为我们是无法精确描述的。如何给出好的边界和初始条件是一件很难的事,他们极大的影响模拟结果。

取单位质量的海水,所以F=ma方程式中,m就省略不研究了,另外一项就是a。


地心引力不变,而惯性离心力随纬度变化,赤道地区离心力最大。



方程的左边和右边就是位势和几何高度,g取9.8时就相等了。注意这个地方的1/9.8是故意这么定义的,用于把g消掉,如果没有这个东西,方程左右两边就是重力位势=重力x铅直移动距离。
这样定义一个位势差(单位为位势米),意在将位势差和铅直移动距离直接数值上相等,非常方便。

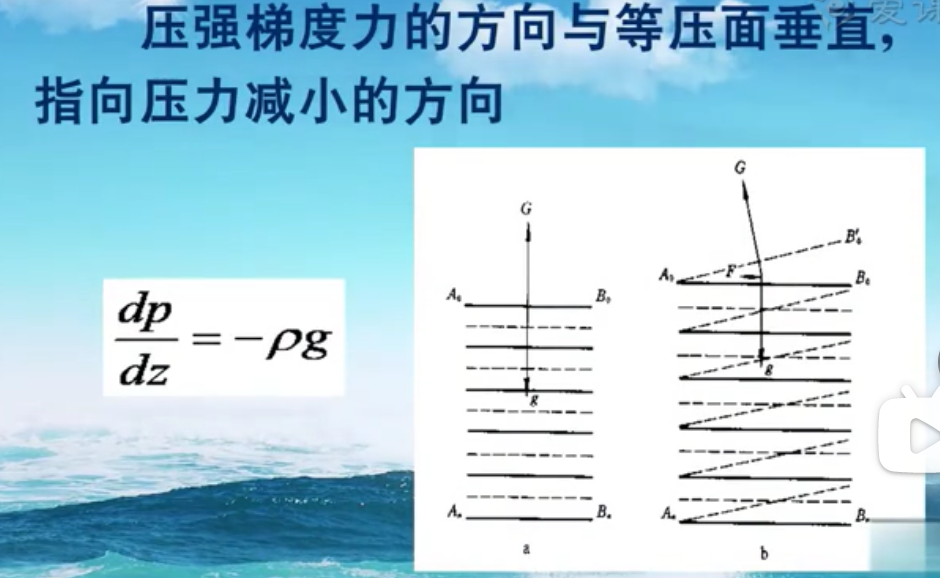
上面a图的意思是压强梯度力和重力保持平衡的状态,b图由于某种原因等压面倾斜(老师没有做更多解释),即当等势面和等压面不是平行的时候,在水平方向上产生一个分力。


等压面没有倾斜,就是和等势面(等势面一定水平,与运动无关)平行。


运动的海洋中,斜压场时常态,但是有的时候可以近似为正压场(正压场是理想状态)。

水平压强梯度力非常小(科氏力也很小),所以一般大尺度长时间的作用下才能显现出来(一个力就是一个加速度,时间足够大,速度就大)。

科氏力是一个假想力:牛顿定律在惯性参照系下才成立,但地球并不是一个惯性系(尤其是研究大尺度运动,地球旋转的效应并不能忽略的时候),而我们并没有非惯性参照系的研究手段,所以只能认为的引入一个科氏力(因为我们严格的定义力的时候是成对出现的,大小相等作用相反,但认为引入的假想的科氏力不是)。
关于惯性系,能查到的大多数定义方法不好理解,在这里简化理解为:以静止或者匀速直线运动的物体(该物体不受外力的运动状态,我们将这种状态划归为物体的本性,称之为惯性)作为参考系,在该参考系下牛顿定律成立。当然,静止或匀速直线运动是一种理想状态,由于自然的极端复杂性,我们必须假设一个理想状态出来。此外,参照系这个词脱离生活后往往不好理解,当我们把思维空间放大到整个地球、太阳系乃至宇宙的时候,就更容易意识到并没有一个参照,或者说并没有一个中心存在,也更容易意识到宇宙的混沌,任何一个物体都在因为各种各样的原因运动,无法精确预测,也不存在理想状态。




地球自西向东转,高处的线速度要大于地面,所以自由落下的物体水平速度比地面要大。此外,我们也可以推出,这个效应纬度越低越强。


注意这是矢量相乘。
科氏力做工吗?:科氏力和运动物体的夹角永远是90°,所以永远不做功。它只改变运动物体(例如海水)的运动方向,没有加速减速作用。

垂向上因为重力非常大,所以fz一般不予考虑。
uvw分别是速度在三个方向上的分量,垂向运动w较小,也不需要考虑

f 中的sin函数在模式中处理起来非常麻烦,可以用泰勒级数展开,我们在实际当中遇到的问题总是有限的,所以其函数也总是收敛的,取展开的前几项就足够逼近原函数









例如风再大,在贴近地面的地方风速也是0,风速在垂向上呈对数分布。



对于符合该定律的称为牛顿流体,不符合的称为非牛顿流体。


风吹海面,但是下面的海水也在运动,除了粘性以外,还有湍流。U是水平运动速度,L是水平运动尺度,v是粘性系数。U一般也不会太大,而L可以非常大,而粘性系数又非常小,这就会造成湍流雷诺数非常大。所以本来我们考虑大尺度问题时和湍流没有什么关系,但是恰恰是因为尺度大造成雷诺数很大,造成湍流非常强,所以这个对应尺度的模式中必须考虑湍流,而湍流的规律就是没有规律,只能想办法近似。湍流问题是方程少未知数多,自由度太大没法解,只能认为的造方程,而不同的人选取的方法不同造的方程也不同,就会引入很多误差。如果错的离谱,也许短时间内没有什么大的影响,但模式运行时间一长,这种错误越积累越大,模式就发散了。
实际上,只要是海洋的问题,雷诺数都会很大。



湍流粘性应力方程中,把一些东西忽略掉以后就是上式。



海水的牛顿运动方程如上式,分别列出了三个方向上的加速度。其中分别考虑了压强梯度力、科氏力(垂向是重力)、湍流粘性力。
上面有三个方程,但远超三个的未知数,所以是不闭合的。
我们通常认为线性的方程是可以解的,而非线性的方程是没法解的(如果其中有一项是两个未知数以上相乘,就成了非线性)。上述方程乍一看是线性的,但方程左侧的加速度,实际上速度分量uvw并不仅仅是t的函数,它还是地理位置xyz的函数,而xyz同时也是t的函数(因为海水是在运动的),所以全微分如下

以上我们列出了运动方程,下面介绍连续方程:

ρ为海水密度

如果散度为0,表示被研究水体没有源也没有汇,不会凭空出现和消失。

密度随时间变化为0,这是一个假设。
由此,我们给上一节给出运动方程又加了一个方程,但即便如此仍不闭合,所以可能还要做其他的假设和简化。
有了方程只能得到通解,通解中还带有一些系数需要确定,这时就需要代入一些确定的情况来确定这些系数,我们通常使用边界条件。



即便如此,运动方程还是无法解出来。
所以还需要进一步近似,首先提出来的近似就是地转流:

将运动方程中的非线性项直接忽略(左边的加速度),令其为0,认为它们在时间上的变化非常小。以及把复杂的湍流粘性应力也不要了。
最后只剩下压强梯度力和科氏力(重力)的平衡。
注意,我们这里省略的是加速度,不是速度,海水在省略后依然是运动的。

从方程的形式上看,我们做了大量近似,省略了很多东西,但是通过观测资料发现,其实差别不是很大。
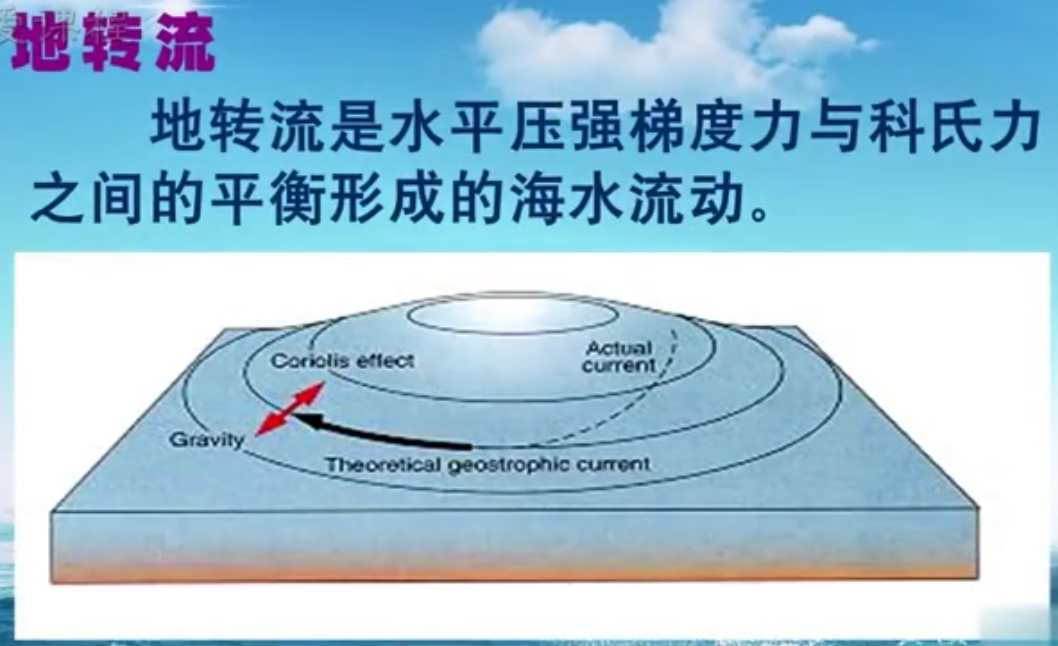
我们之前讲过,任何一个参数有极值区域,说明是有运动存在来维持的,否则就自然消散平衡掉了。
中间区域产生过一个较强的压强梯度力,而顺时针旋转提供一个向中心的科氏力与之平衡。
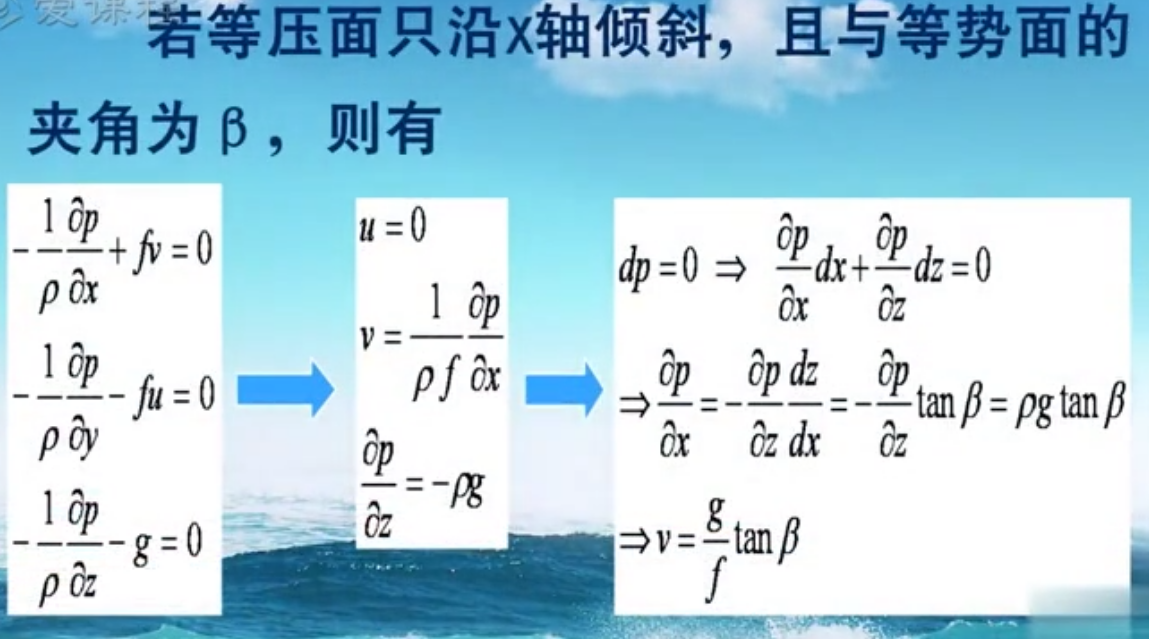



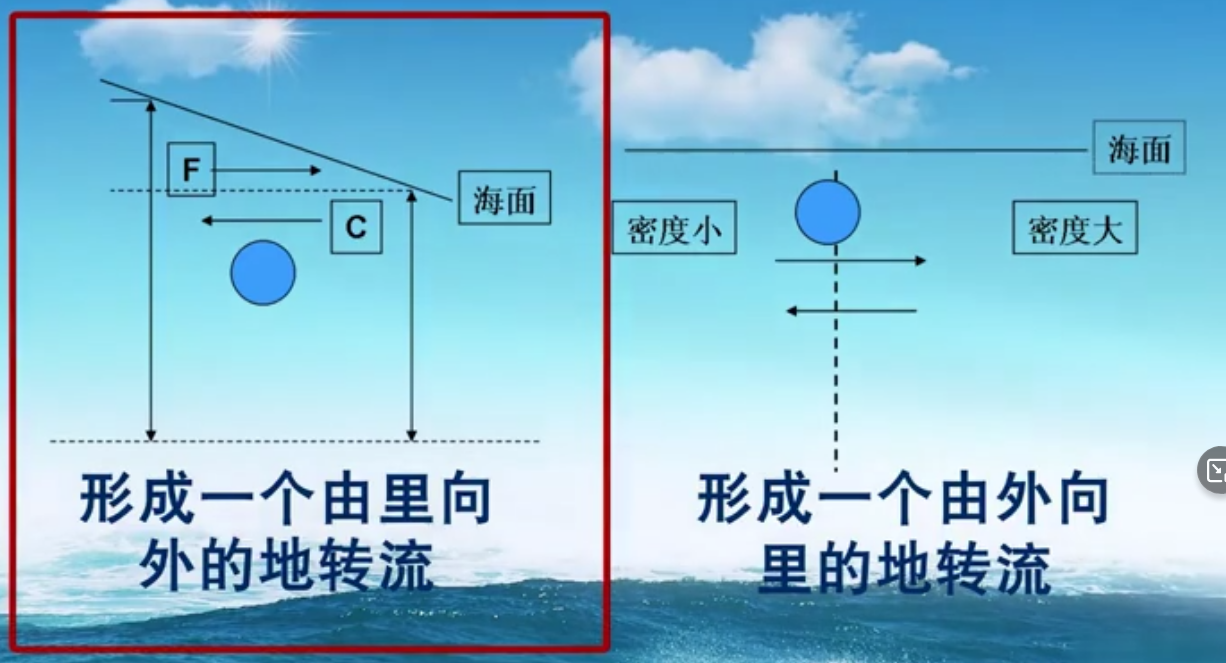
上图是外压场和内压场。
地转流我们刚提出来的时候就说过,这是忽略了很多东西的近似。当我们考虑问题的尺度越大就越接近地转流状态(例如大洋环流),因为这两个力都很小,需要慢慢的起作用,我猜这里面可能还会因为小尺度随机的东西都被忽略了。
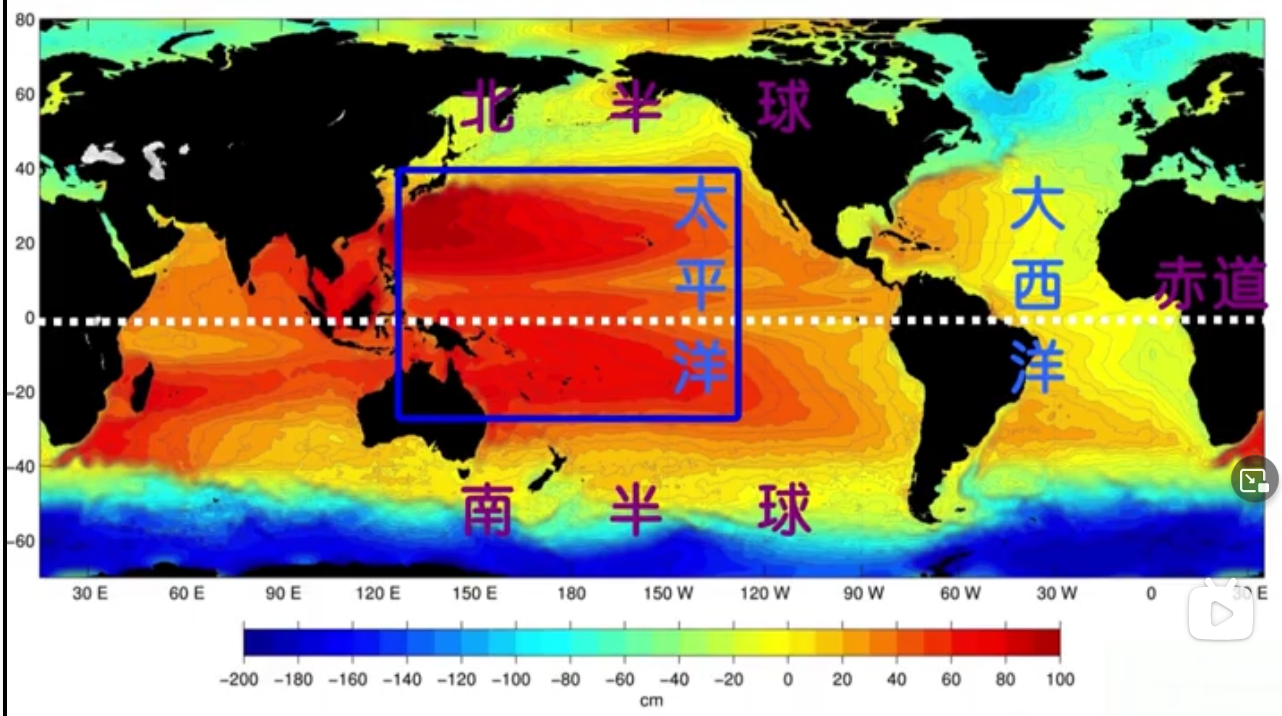
上图是卫星高度计实测数据
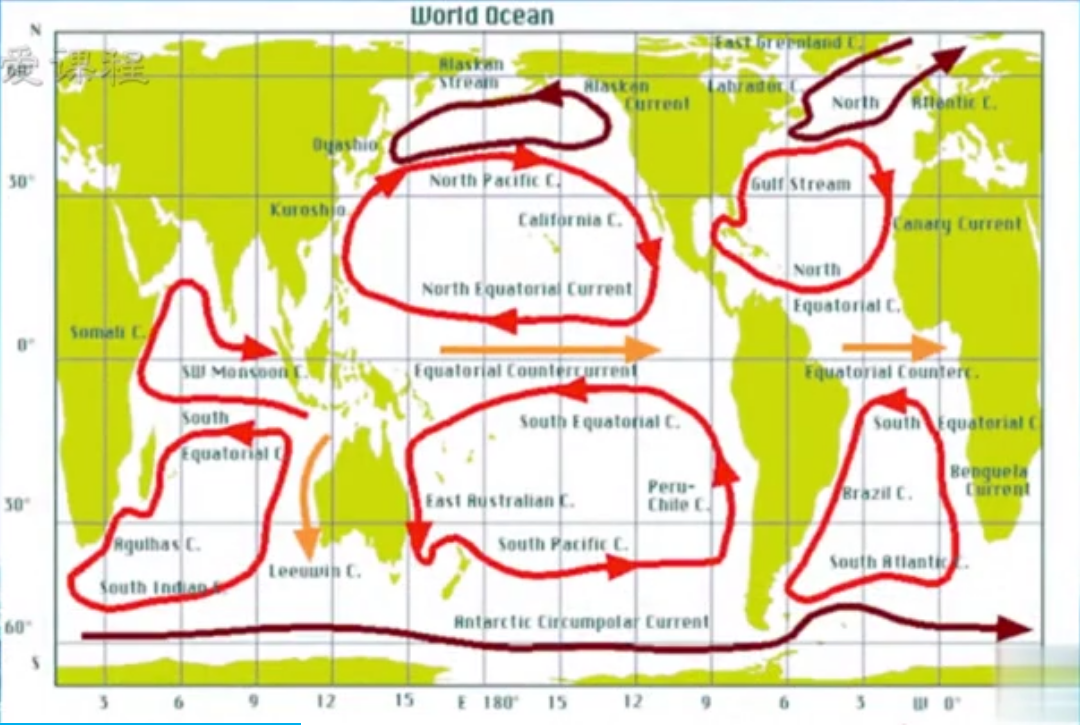
实际高度能够和大洋环流对应起来(地转流理论)
虽然地转流在大尺度上解释了如大洋环流等一些现象,但是在细节的海水运输上,无法解释所有的现象,存在矛盾,所以就需要有其他的理论补充,这里引出风生埃克曼漂流。

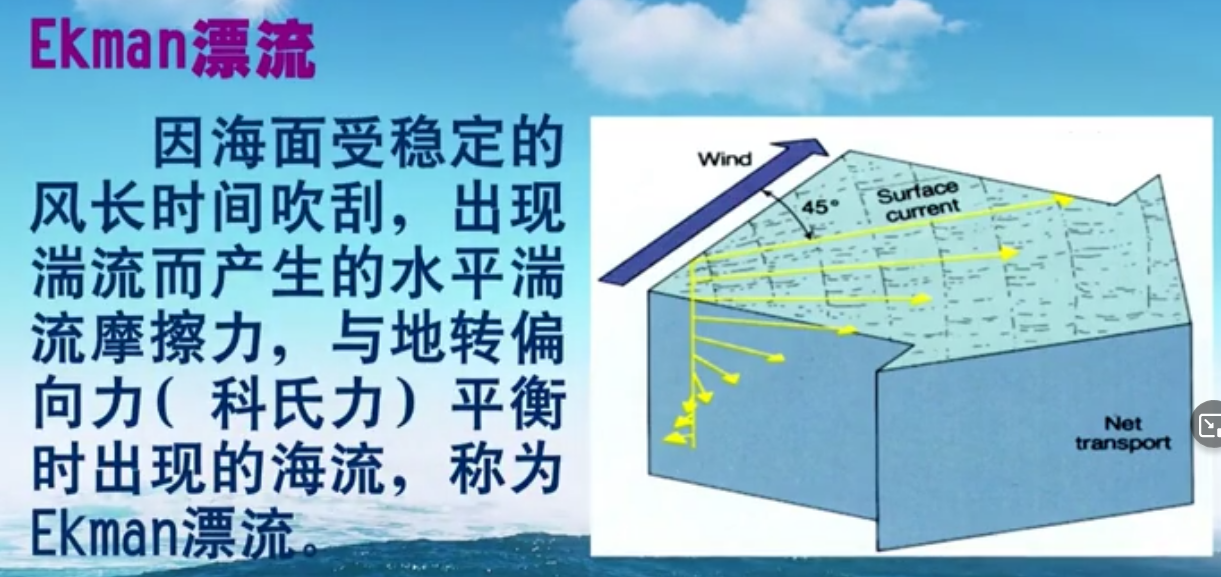
注意,我们在学地转流的时候是水平压强梯度力和科氏力的平衡。
而这里,我们考虑的是湍流粘性力和科氏力的平衡,因为这里的尺度要小一点,压强梯度力忽略不计。
上图右边是一个艾克曼漂流示意图,表层水与风向成45°角,这个角度越往深越大,到底层的时候甚至是风向的相反方向,当然越深流速是越小的。


摩擦深度也成为埃克曼深度。

Kz粘性系数,f科氏力参数
与粘性系数成正比,与科氏力成反比,比较好理解。科氏力越小深度越深。


U10是还表面风速,V0是海水运动速度,D是深度。
注意,我们之前还学习过混合层的概念,混合层和埃克曼层是重叠的。

由于埃克曼主要是和风有关系,所以我们还需要重点看之前的风是怎么讲的
我们之前讲赤道地区有贸易东风,但实际上偏南北的区域也不完全是东风
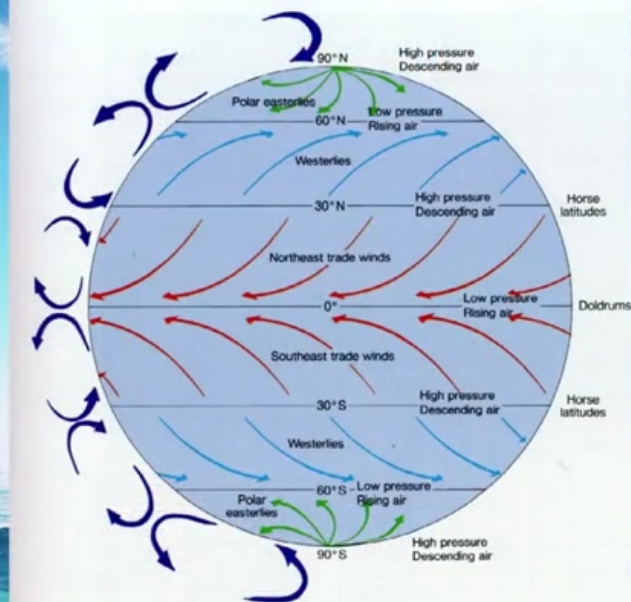
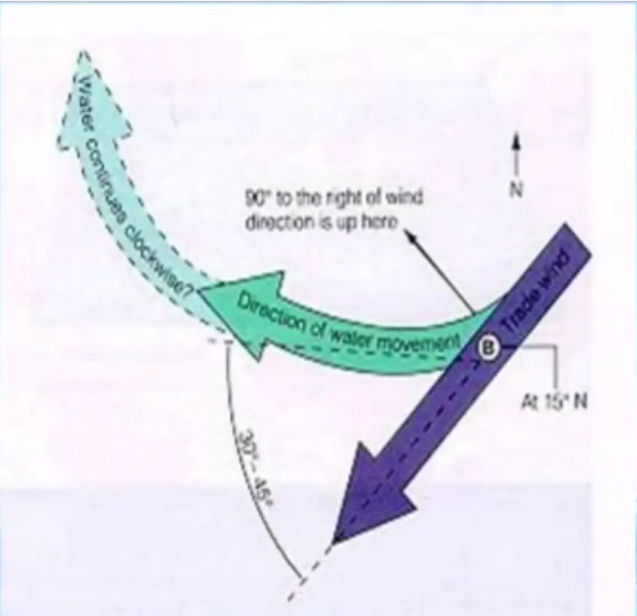
风一吹海水就要动,海水一动就要偏转,如上图,形成埃克曼流。紫色是风,蓝色是海水。
这其实就和地转流方向是一样的,支持着大洋环流。
也就是说,你提出来的新东西和大家普遍认为是常识的东西不矛盾,是比较好的。

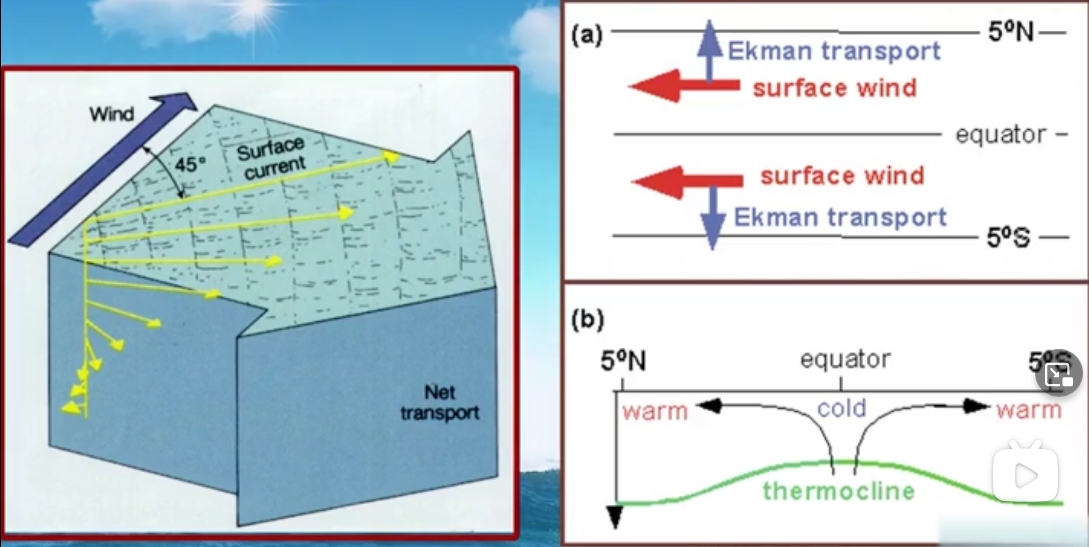
如图所示,整体来看,海水的输送是风向右偏九十度(与科氏力方向一致)。注意,这里说的是海面的海水受到的科氏力,我们看到埃克曼流在每一层的方向是不一样的,所以不要认为这个输送方向与直观上有矛盾(直观上认为海水输送方向应当处于风向和科氏力合力方向)
北半球海水往北,南半球往南,根据质量守恒,赤道中间的海水只能从海底往上补充。

在中纬度的风是西风,将海水往南输送,这就造成副热带有一个辐聚区,所以副热带海区海面较高,这又形成了压强梯度力。
通常来说,表层水的营养较容易耗尽。有上升流的地方将海底的营养输送上来,一般生物更多。而副热带海区由于是辐聚区,都是表层水,相当于海水中的沙漠。

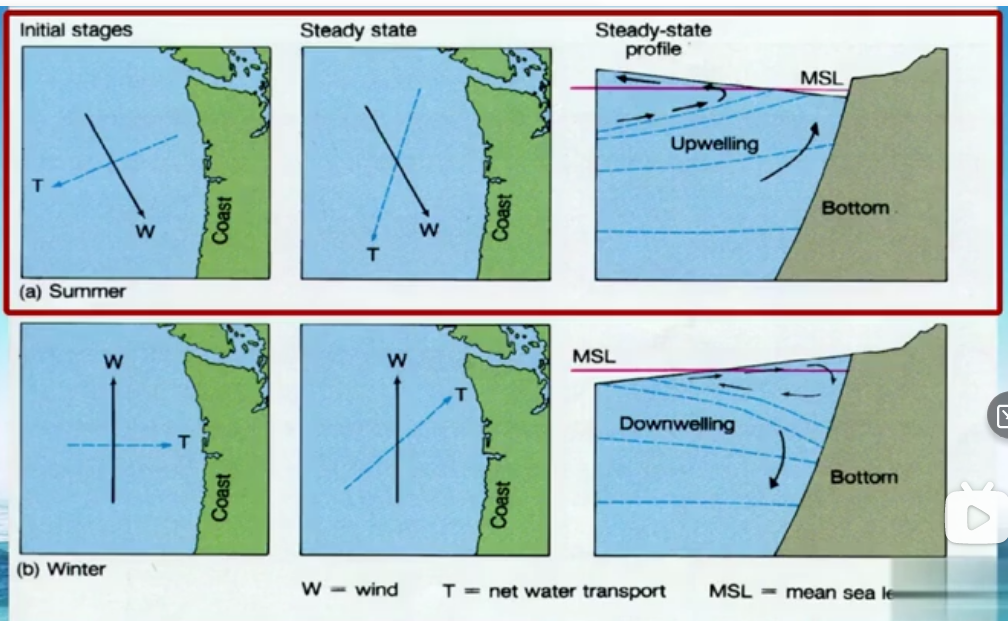
上图中黑色箭头代表风,蓝色虚线代表海水输送方向。右边展示了两种情况,即上升流和下降流。
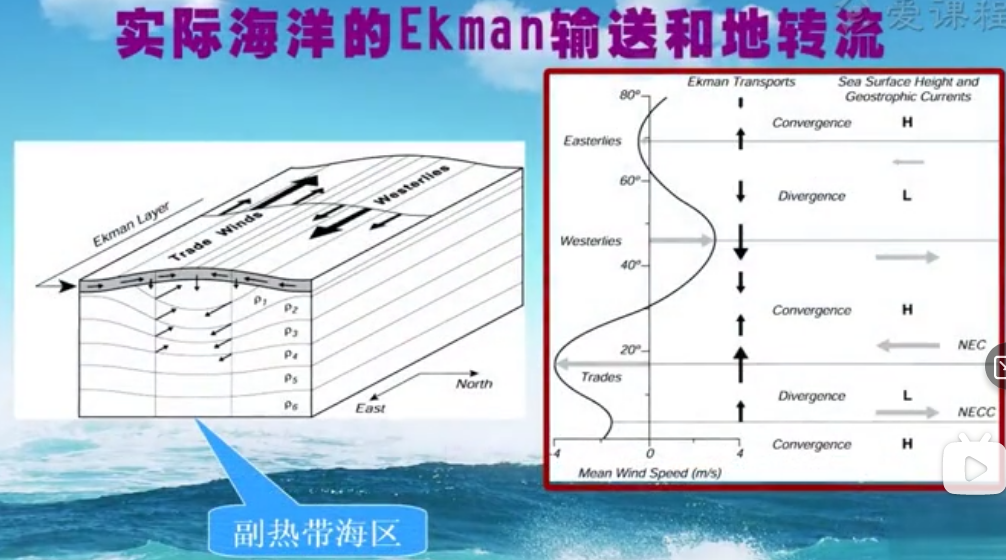
右图是北半球的埃克曼输送图
看箭头标出了辐散和辐聚区,辐聚区的水比较高,需要有一个流来维持它,就是地转流。辐散辐聚区又会有上升流和下降流,
一般说埃克曼的影响因子,我们讲科氏力和湍流粘性力,风应力只对表层起作用,所以埃克曼流我们说是湍流粘性力在起作用。埃克曼通常是比较薄的,因为风应力对海洋的影响有限。


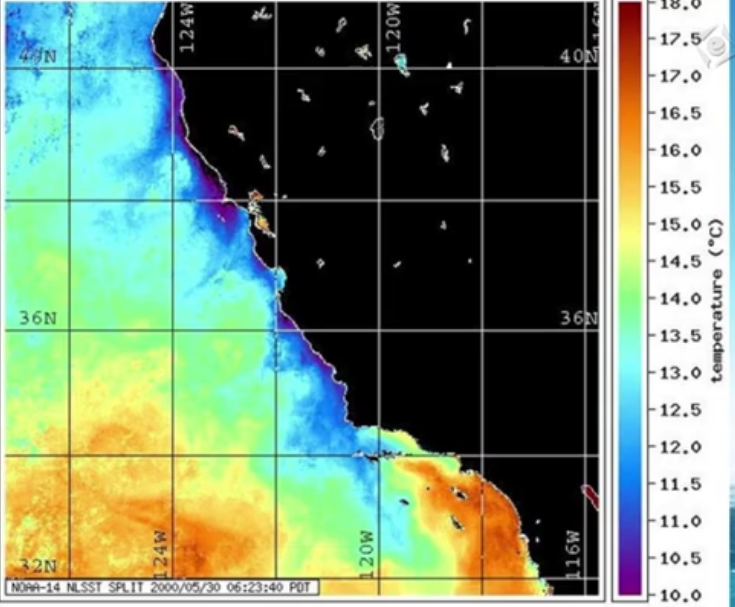
上图沿岸水温较低,可能是上升流,所以这里可能吹北风,艾克曼漂流往西。

台风中心是低压区,所以气旋是逆时针。根据埃克曼漂流理论,海水从气旋中心向外侧输送,所以气旋中心就会出现一个非常强的上升流(因为向外侧输送是所有方向上,所以需要大量海水补充),造成台风的冷尾迹。
一般来说在海水表层用艾克曼漂流,深层用地转流解释。

将两种输送公式结合就是黄色公式,其中有一个风应力旋度,所以最终决定大尺度大洋环流形式的,不是风应力本身,而是风应力旋度。
我们现在通常认为,风是大洋环流最原始的驱动力,海水运动起来以后又受各种各样的力的影响。
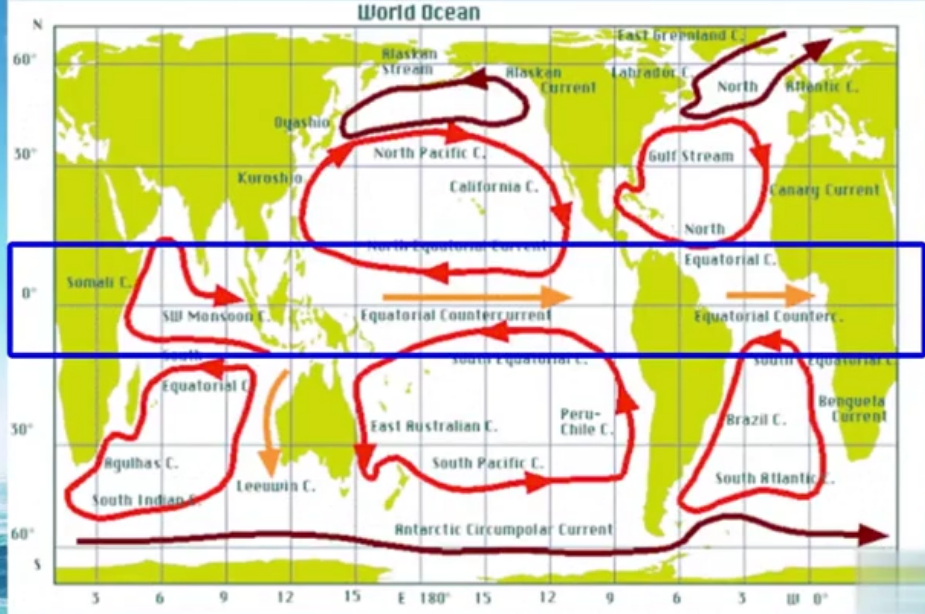
我们都知道赤道地区有贸易东风,但赤道上却又有个向东的流,称为赤道逆流。
我们之前看过副热带高压区在大洋上不是对称的,是偏西的,反映在海流上就是西边界流非常强。例如太平洋的黑潮,大西洋的湾流。我们称为“西向强化”。
以上说的两个问题都是埃克曼流和地转流没法解释的现象。

以上三人虽然方向不同,但都可以逻辑自洽。我们现在通常认为第二比较可信,同时也更容易处理。他们三个人基本奠定了大洋环流的所有理论。


上述公式即把地转流和埃克曼漂流放在一起考虑,在计算上增加了许多难度。
过去没有计算机硬算,所以必须给出解析解,对数学要求极高。

对两式同时积分(积分是为了简化问题,忽略细节),得到海水输送的质量。
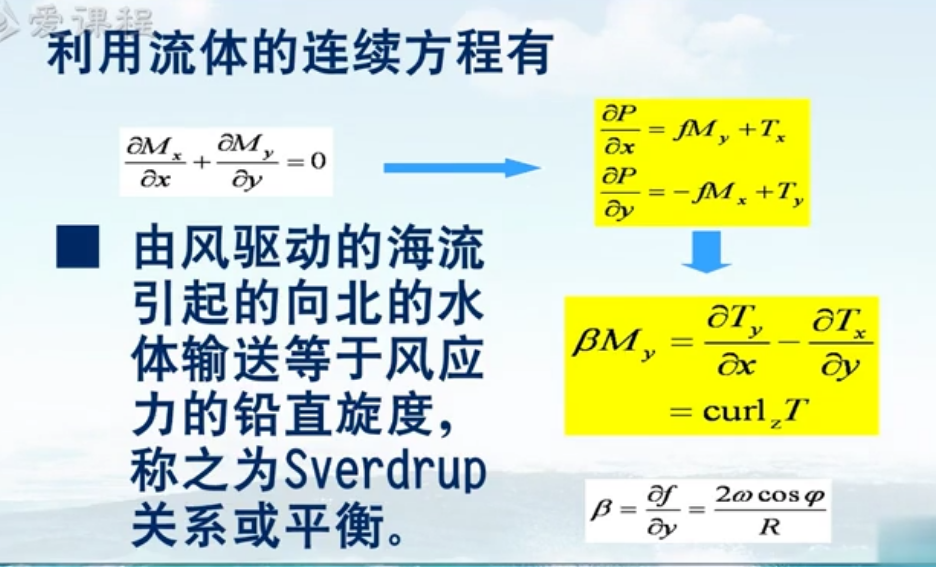
用连续方程继续化简,最后得到质量输送与风应力旋度有关。该式在大尺度上基本成立,尽管它在推导过程中简化了许多东西。
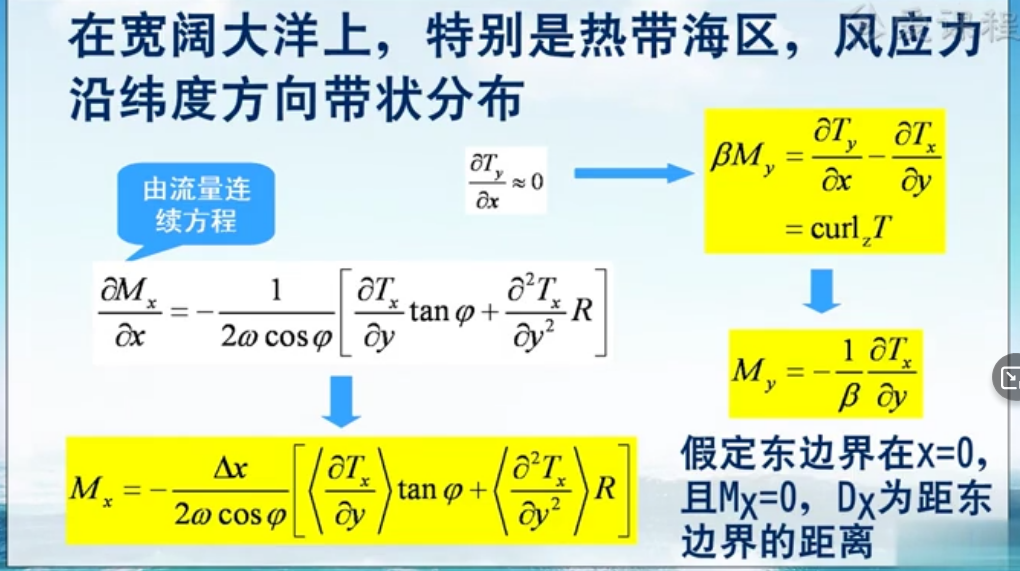
其解析解如下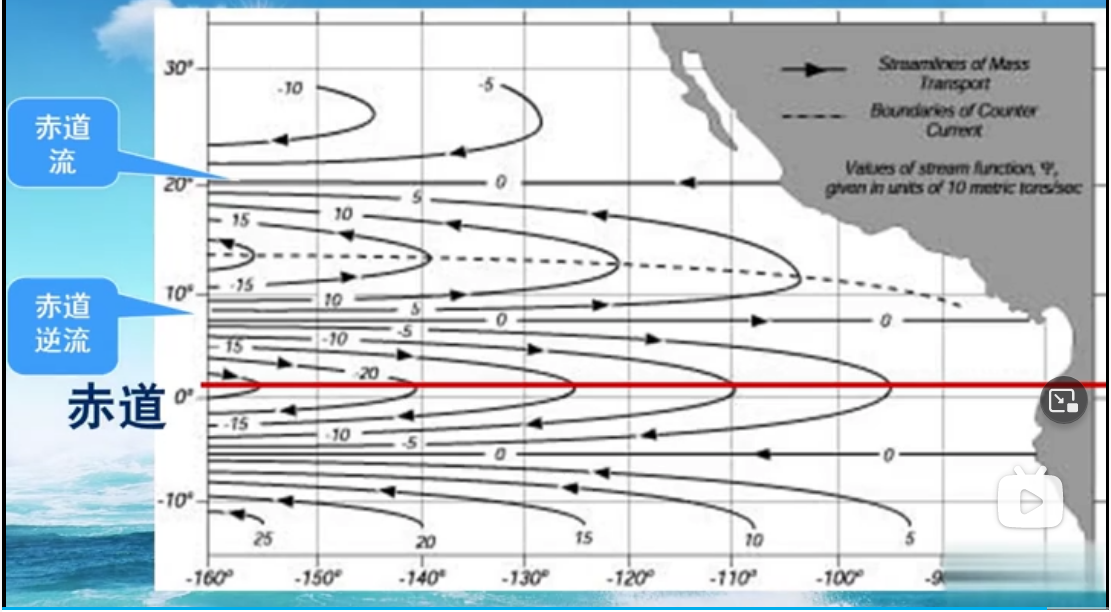
该解至少给出了赤道逆流,与真实情况差不多。



相比于Sverdrup,Stommel多加上了一个海底的摩擦力。
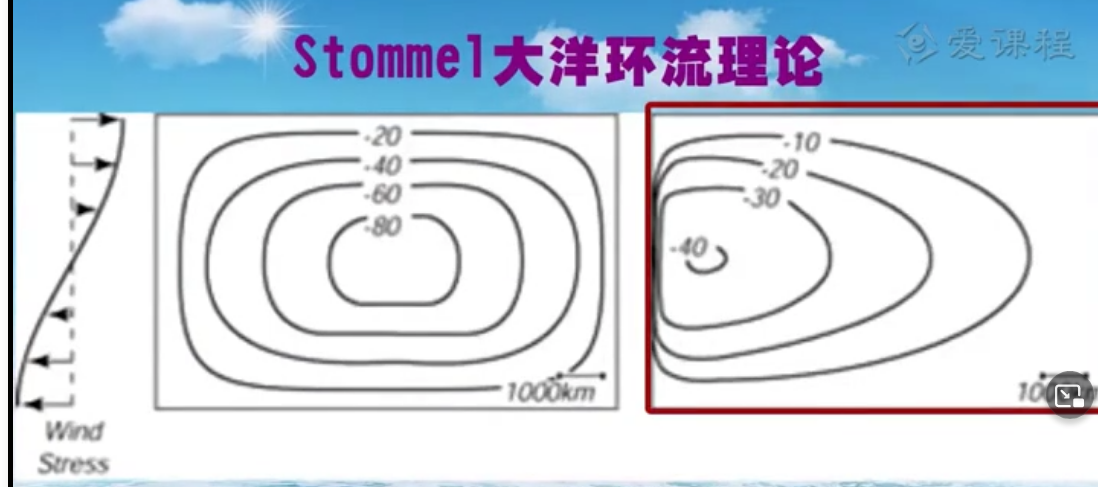
当科氏参数f随纬度变化(高纬度科氏力大),就自然的能得到西边界强化 。

Munk又加了一项海岸侧摩擦。(没有科氏力随纬度强化)

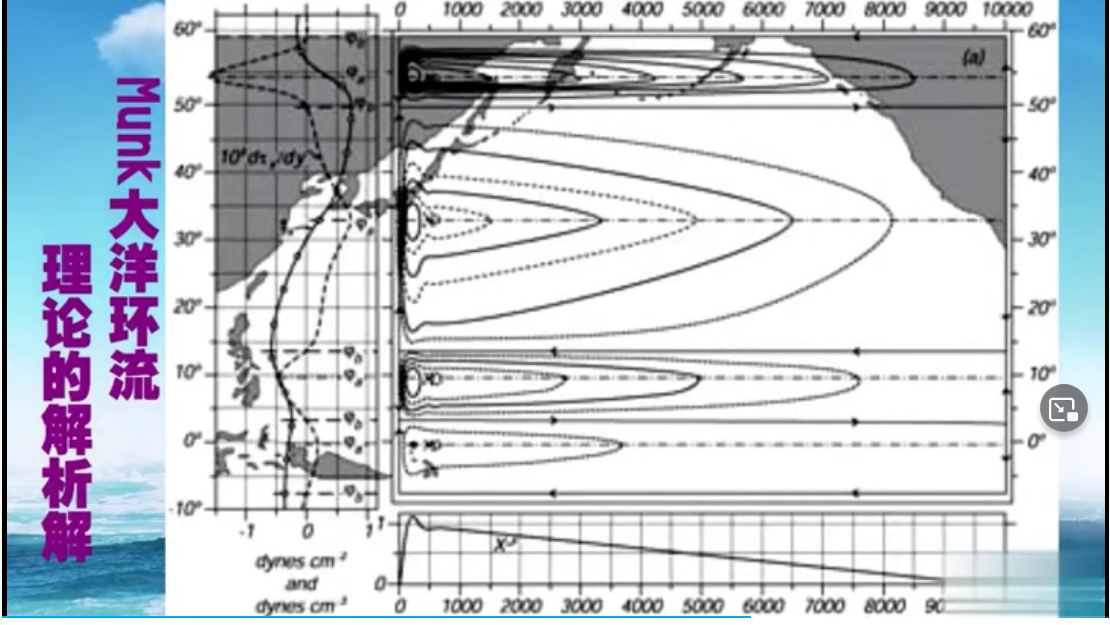
因为测摩擦不容易考虑,而科氏力无论如何都是要考虑的,只是变化不变化的问题,所以一般情况下我们选择考虑科氏力随纬度的变化。
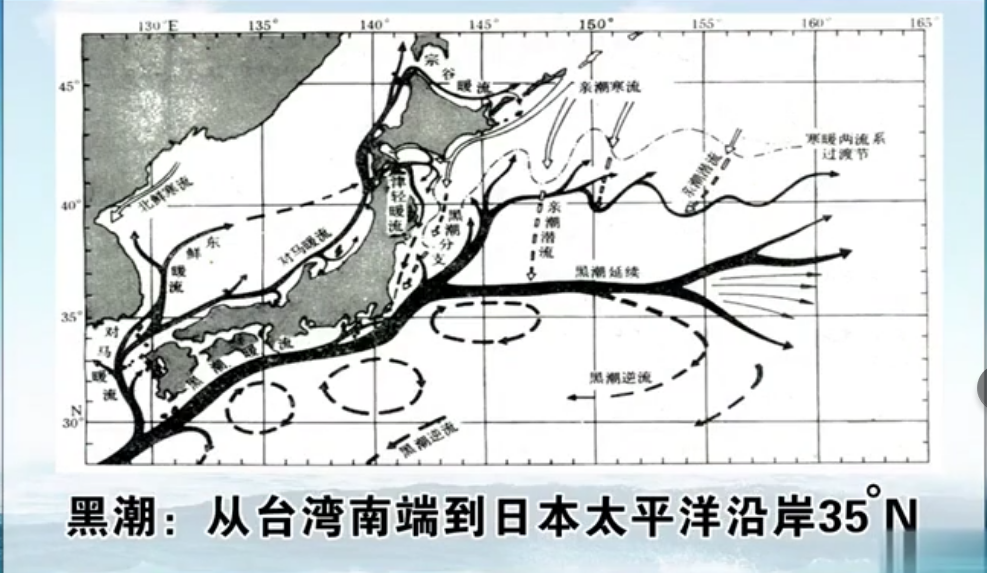


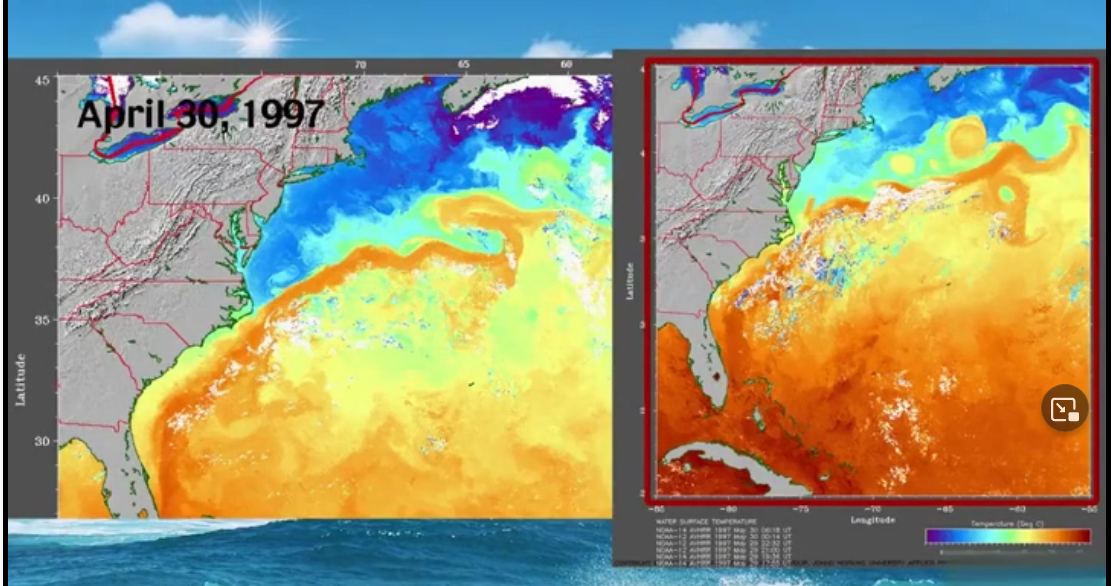
在此之前,我们只关注了大尺度的大洋环流,在海洋中还存在大大小小的涡(上面黑潮那个图就有)。整个海洋是一个非常强的湍流系统,我们不能认为湍流都是小尺度的东西,实际上任何尺度的都可以叫湍流(大洋环流也是湍流系统)。因为大尺度平均以后可以比较简单,容易把握和了解。而小尺度的往往变化更快,不容易把握,所以我们提到的小尺度湍流更多。


因为地球本身在转,所以每个东西都在转,转的快慢我们称为科氏参数。

行星涡度是每个物体都得转,相对涡度是确实自己也在转,相对地球的旋转。

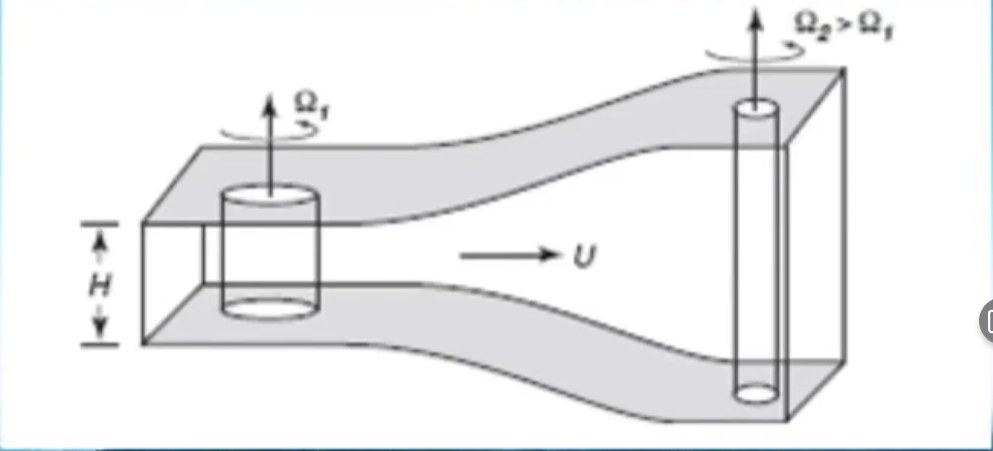
在浅水中旋转到深水中,相对速度会增大(这个旋转相当于被拉长变瘦了)。
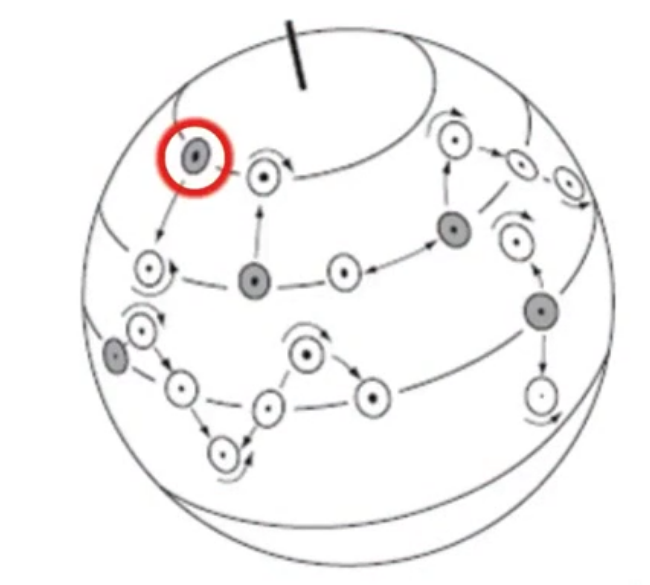
行星涡沿维度变化较大。从高纬到低纬减小(f减小),为了角速度守恒,所以要转起来。注意图中灰色是不转的,白色是转的,各个纬度不转的涡旋改变位置后可能都会转起来,因为涡旋的方向有正负。绝对涡度不变的情况下,行星涡度和海水深度在变化。绝对涡度/海水深度=绝对位涡。



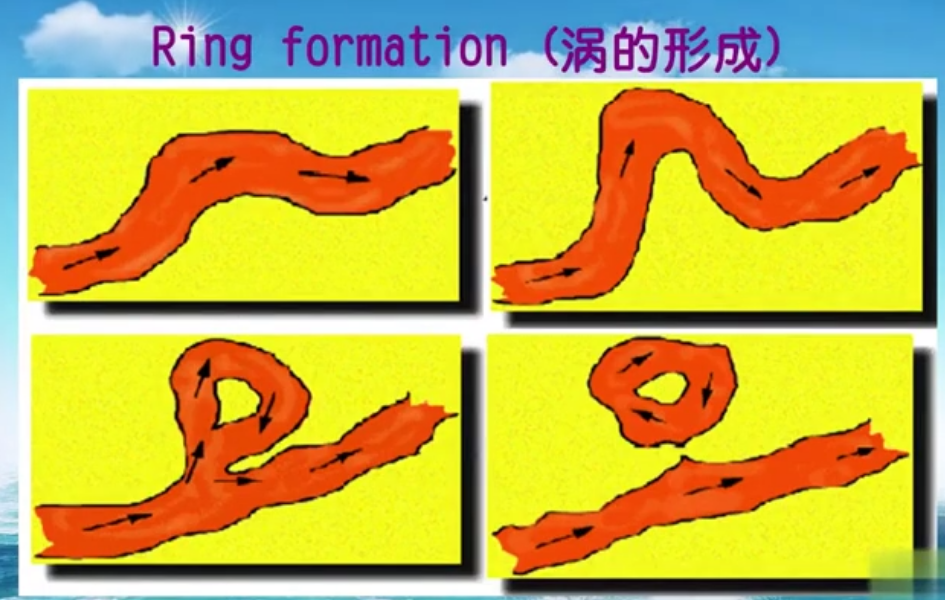
肯定不是所有涡都是这样形成的,真正的原因会非常复杂。上图也是一种合理的机制,所有的机制都不好验证,包括以上的机制也是没法验证的。
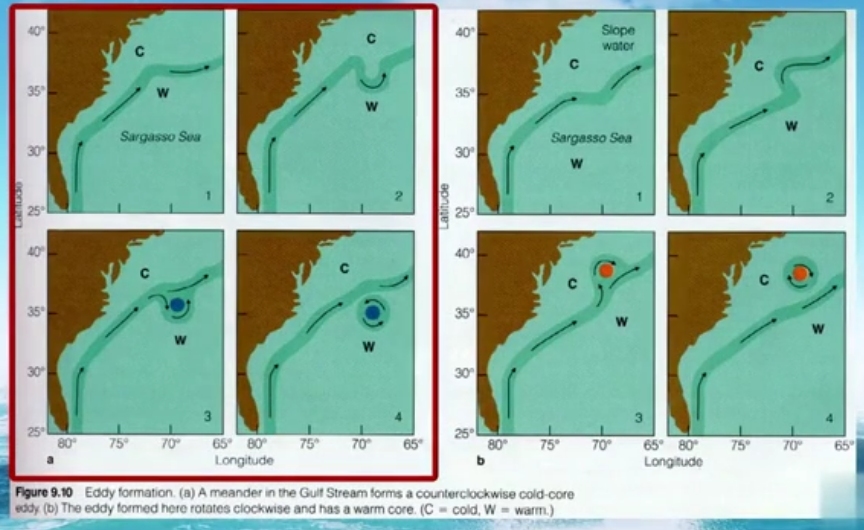
再次强调冷热都是相对的,并且是在当前条件下不正常的情况,才称为冷/热。
注意这个冷涡方向是正的,暖涡是负的,没有例外。
冷涡是低压区,暖涡是高压区
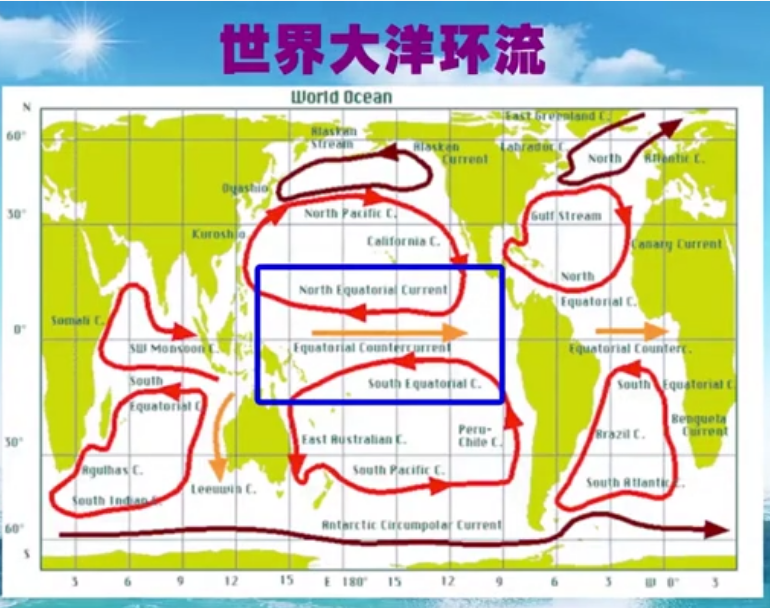



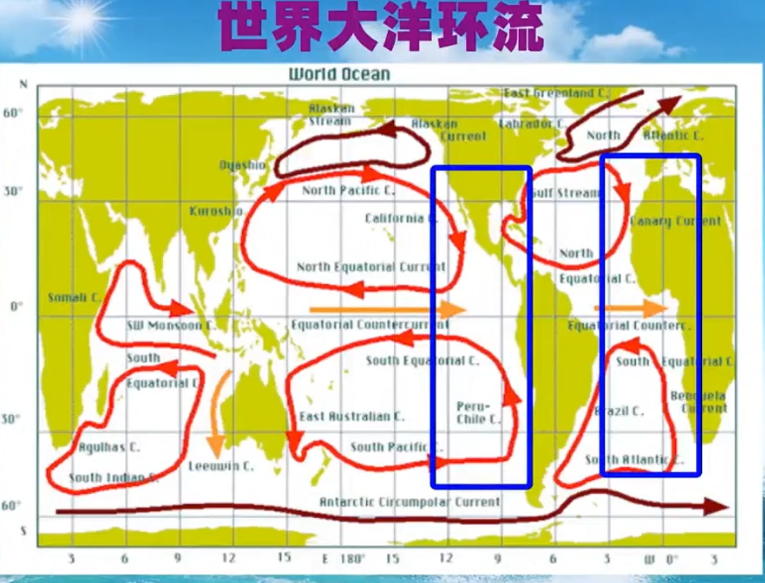
东边界这几处都是上升流区域。
原因我们考虑埃克曼漂流,因为地转平衡是水平流。
例如太平洋东边界,吹东北风,向西输送海水,所以岸边从下往上补充海水。
由于高纬度寒流吹向低纬度,使大气层结较稳定,有利于海雾形成。(有雾的大气情况一定是稳定的,因为蒸发的水汽走不了。最简单的就是风吹雾就跑了,或者太阳照射,使得底层大气不稳定,压强变低,形成对流)

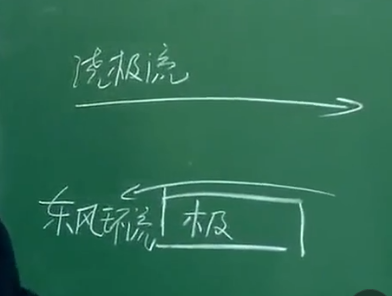
南极洲外围是东风环流,再外围是绕极流,因为动力作用(埃克曼漂流),中间形成一个辐散区(注意这是南半球),也就是要有上升流,营养富集,二氧化碳浓度极大。
之前讲过南极水是海洋底层水,因为本来温度就低就要下沉,东风环流又加强下降流。
深层水是大西洋下沉的。
绕极流再往上就是赤道流了。

辐聚区要形成下降流
热盐(子午翻转)循环
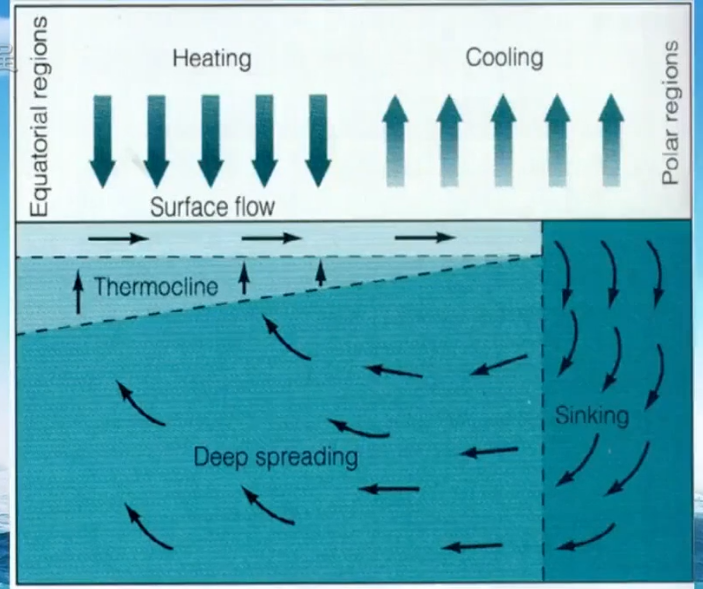
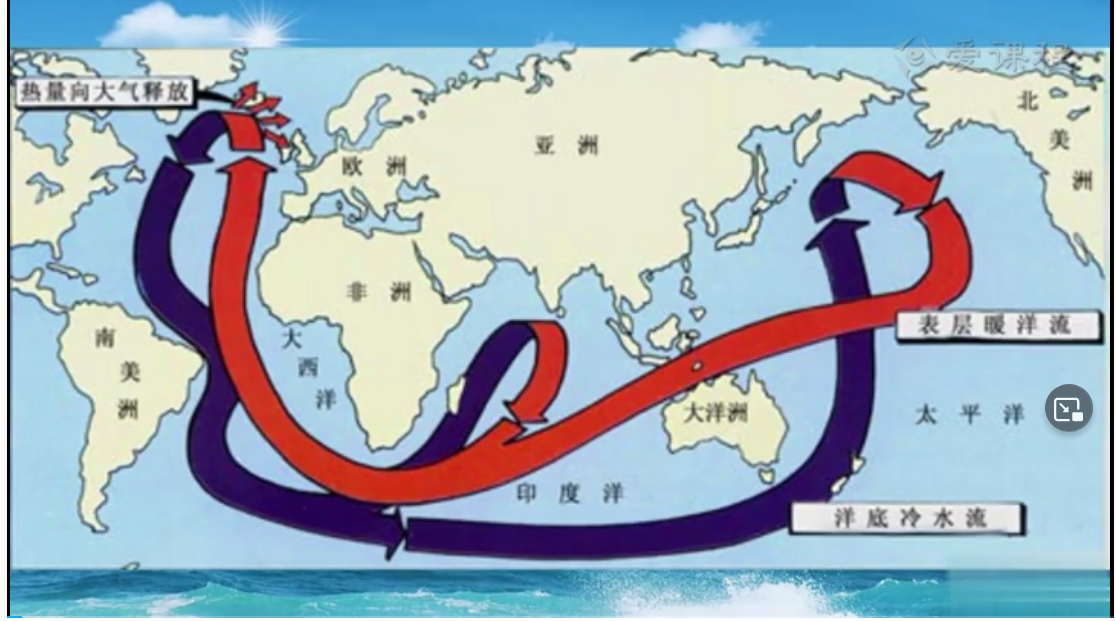
上图蓝色表示深层水,红色表示表层水。从左侧大西洋下沉的水到达南极洲大概需要七百年,再向东到达澳大利眼南端需要六百年,北上到达太平洋北部又是七百年。这个缓慢的大循环无法用仪器测得,只能用化学的同位素方法测量。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号