概述
1.确定信号与随机信号
确定信号:可以确定时间函数表示的信号。学习确定信号的处理方法是基础,处理随机信号时使用的是相同方法
随机信号:信号不能用确切的函数表示,只可能知道它的统计特性比如概率。
2.连续信号和离散信号
连续信号:在连续变化的时间范围内有定义的信号即连续信号,若其函数值也连续则为模拟信号。
离散信号:仅在一些离散的瞬间才有定义的信号即离散信号,当其值为规定数值时为数字信号。
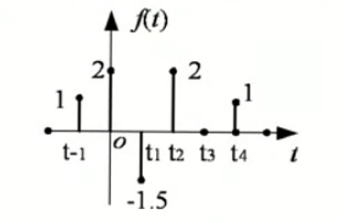
注意理解下图这种才叫离散的瞬间才有定义的离散信号。为了方便计算机处理,这种信号一般由模拟信号采样取得,当采样的间隔为等间隔时,我们也称该信号为序列。
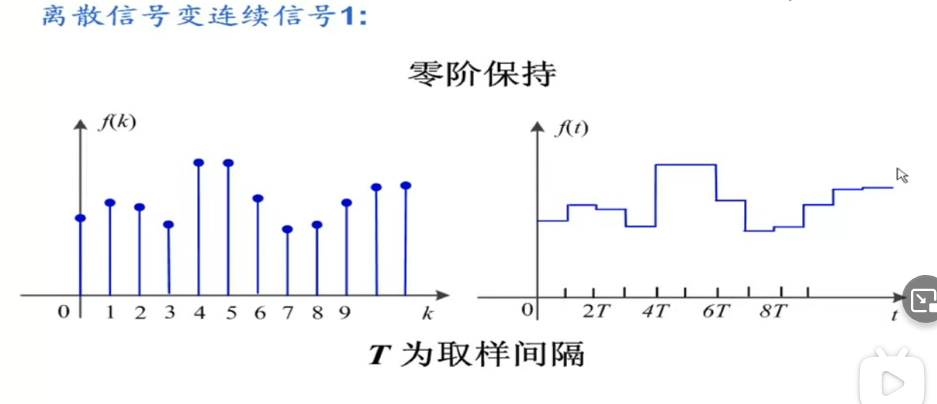
离散信号变连续信号的方法:
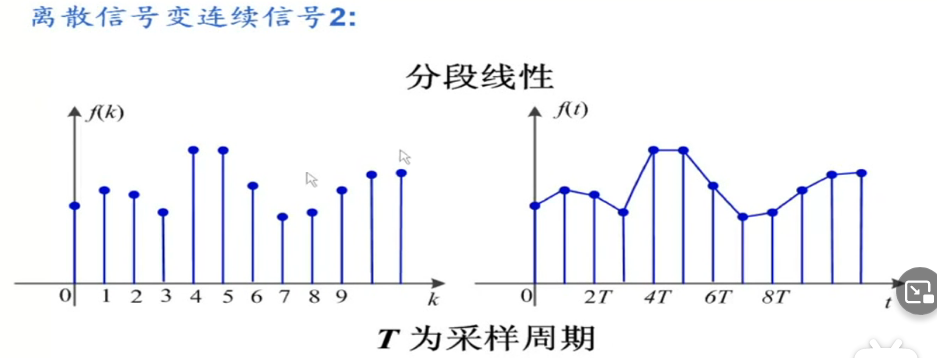
3.周期信号和非周期信号:是否按相同规律重复变化

实际就是两个信号的周期有最小公倍数,则合起来就是周期。

这两个公示是根据电阻上的功率公式推出来的。
我们讲能量有限的信号简称为能量信号,因为平均功率公式中分母T趋于无穷大,所以分子有限时,算得的平均功率为0。
当能量为无穷大时,一般也就是该信号在无穷区间上有定义,为了方便比较两个能量无穷大(无穷大和无穷大无法直接进行比较)的信号,定义了平均功率。此时功率一定是有限的,简称功率信号。

此处是上面讲的两个概念在离散信号上的公式。注意,求和和积分是同一个概念,积分的离散化就是求和,求和的连续化就是积分。


规定观察时刻为t=0,在观察点以后产生的信号就是因果信号,在此之前无信号。相反的就是反因果信号。
注意,信号与系统课程有一条主线,三个关键问题
1. 基本信号及其响应:认识和熟悉基本信号
2. 任意信号的分解:将任意信号想办法分解为基本信号
3. LTI系统分析:求和
其实也就是积分的思想,或者说求圆面积用无数个三角形逼近的思想。
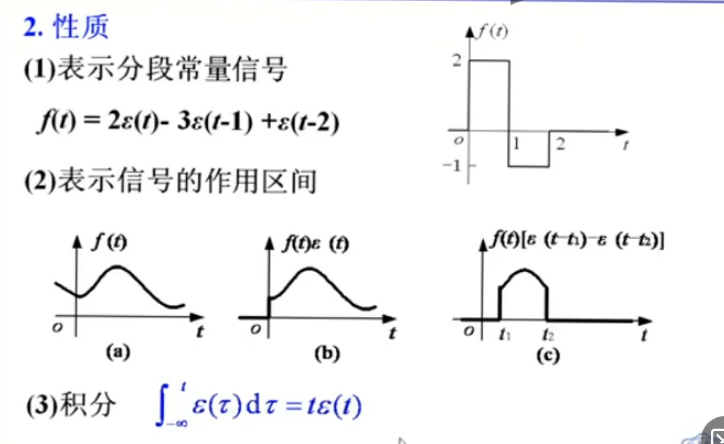
阶跃函数(信号)

这样的定义很巧妙,主要是为了表达信号是连续的,t=0时刻信号突然跳跃,你可以认为它是0-1之间的任何值。
注意,这里和高数中定义函数的习惯略有不同,我们曾经认为这种间断点是不可导的,但是这里我们可以对t=0求导,其导数是下面要介绍的冲激函数。
冲激函数

左上的图是刚才第一张中定义阶跃函数的那个图,信号从0变到1,中间有一个过渡,当过渡的这一段时间趋向于0,就是左下的单位阶跃函数。这个趋向于0的过程中,中间信号的斜率越来越大,如果对其求导就是右上这张图,变化前和变化后导数都是0,当变化的范围逐渐缩小,其导数也逐渐趋于无穷大。所以左下角的阶跃函数求导,就是右下角的单位冲激函数,该函数在t=0时等于无穷大,其余位置为0.

注意单位冲激函数的定义式,用积分为1来定义,也就是上图中右上的那张图的面积为1,即当时间范围趋于0时,只有高度无穷大才满足该条件。
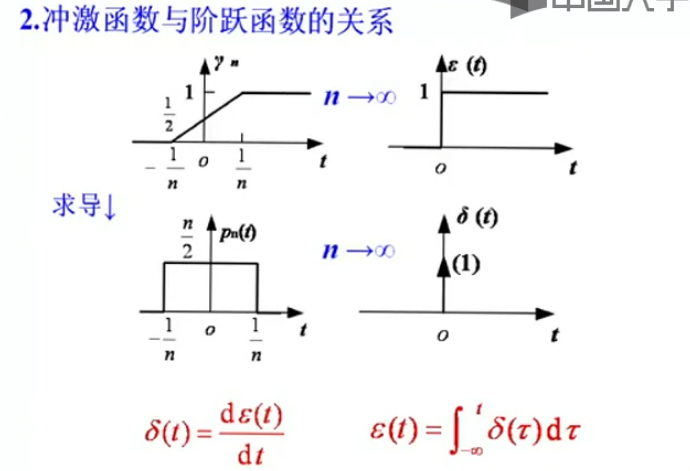
该图就是上面老师板书画的图,这里注意标红的两个关系式。

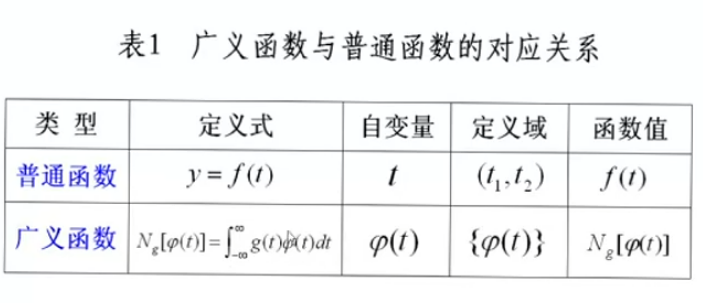
首先理解广义函数的定义:类比普通函数的自变量是一个实数空间,而广义函数的自变量(检验函数)是一类函数。普通函数由一个值映射到另一个值。广义函数也是一个映射,由蓝色公式定义。即由检验函数根据一个新定义的运算规则后,得到一个值。

看这里是如何定义δ(t)的:任何的δ(t),它能够通过函数之间的相互作用(定义式中与φ(t)先相乘后积分)之后,得到φ(0),这样的函数δ(t)就是冲激函数。
这是比上面的描述性的定义更为严格的定义。
含义最后一句话说的取样性质就是说把φ(0)给取出来了。
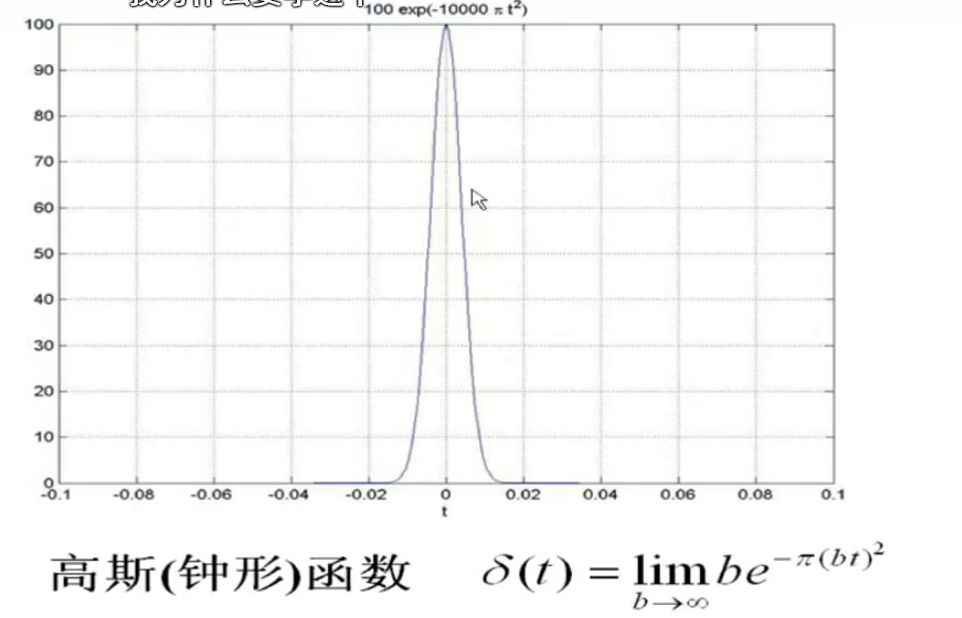
注意,δ(t)是一个理想信号,现实中可以用这两个函数取极限求出来。

首先,由于δ(t)的积分是1,所以第一行的式子两边积分就是第二行的式子。
第一行公式的理解:因为δ(t)除了t=0以外其他δ(t)都是0,所以最终也就是f(0)δ(t),即是说,f(0)倍的δ(t),f(0)表示了δ(t)的强度。
下面例题主要用了采样性质,和δ(t)的积分需要考虑区间的问题,包含0则积分为1,不包含0则积分为0,右下角那道题等于0。
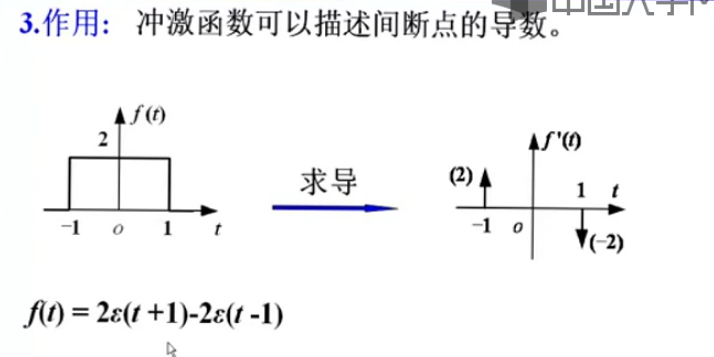
注意第一行的例题中有个阶跃函数,求导为冲激函数。


对冲激函数再求导,得到的函数叫冲击偶。注意理解冲激函数是连续的,所以冲击偶在t=0时冲到无穷大又冲到无穷小。
冲激函数的积分是1,冲击偶的积分是0。
一般连续的信号我们称为函数,离散的我们成为序列。以上讲到的阶跃和脉冲信号都有序列的版本。


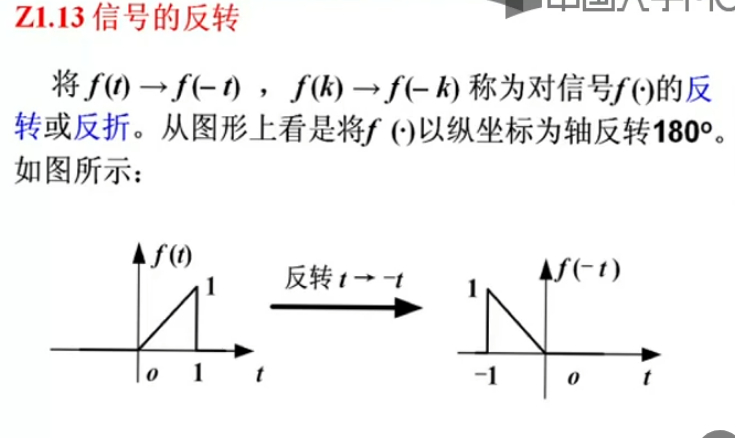
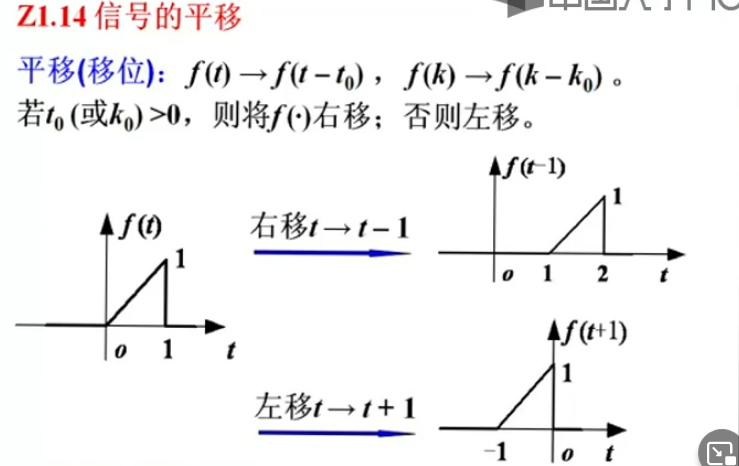
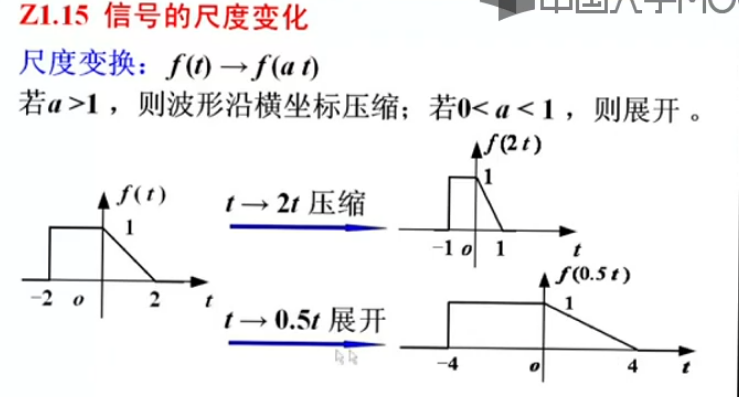
尺度变换,实际就是压缩和拉伸。把握一个f(t)和f(at)中的t和at的作用是一样的,而t又是坐标轴,所以a就影响了信号的尺度。
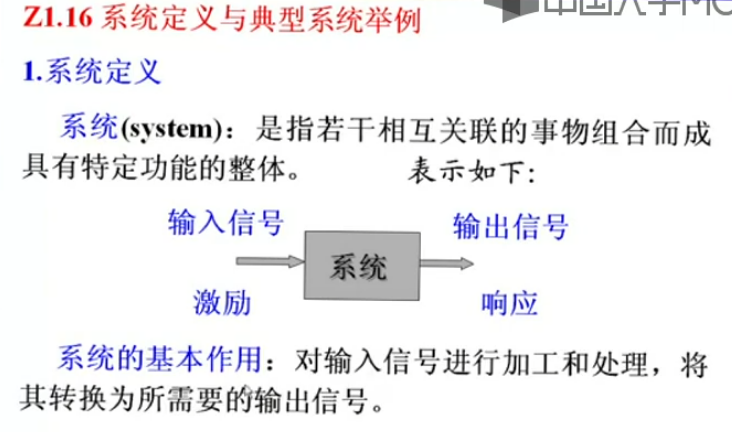

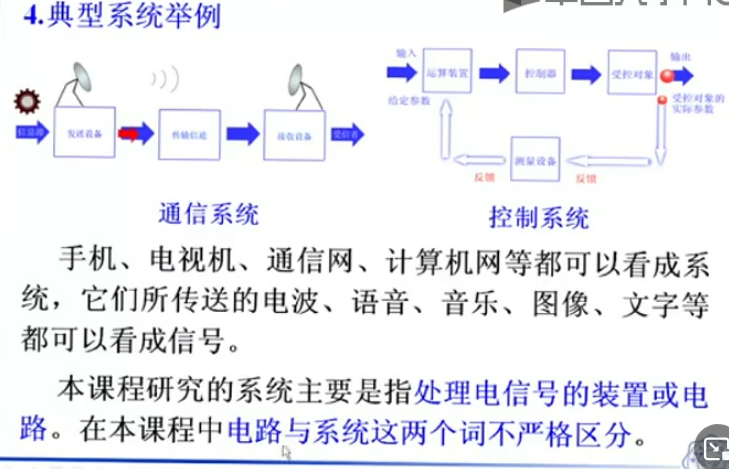
注意,本课程系统主要指电信号的装置。

线性判断:输入的线性组合产生响应的线性组合。
最下面一行的·表示可以t也可以是k,即可以是连续的也可以是离散的。

注意之前的定义是零状态响应,也就是无记忆系统的。这里讲的是动态系统,有记忆的。

时不变就是,任何时候给系统一个激励,响应都是一样的。例如任何时候去按动开关,灯都会亮
本课程主要讨论线性时不变系统,LTI



