HashSet的实现（上）

要理解HashSet，可以按字面上把它分解为两部分，一方面它表示一个集合（Set），另一方面，它的实现使用了散列法（Hashing）。

集合（Set）

还记得吗？在中学里曾经学过，集合是某些指定对象的全体，集合的三个性质是确定性、互异性和无序性。本文提到的集合正是这个数学概念在计算机中的实现。

说到集合，可能你会想到Collection这个词，以及.NET中的ICollection<T>接口，它们通常也被解释为“集合”，不过它们和Set有明显的不同。Collection可以看作是一组数据项的容器（Container），它与数学中的集合概念无关。同时，Set是一种特殊的容器。也就是说，Set的概念更强一些。在本文余下的部分，用集合表示Set，容器表示Collection和Container。

这里比较值得关注的是互异性，在开发中有些时候需要这样的一个容器。我们经常使用的数组和List<T>本身不能满足该性质。.NET3.5之前没有一个类型是直接提供这种支持的，一种方案是采用Hashtable或Dictionary，在存储数据项的时候，只使用key，value忽略。.NET3.5（以及以上）提供了HashSet<T>泛型类，终于可以满足集合的要求了。

集合作为一种数据结构，它的主要操作很简单，最重要的是添加和移除元素，以及查询（判断某个值是否在集合中，枚举集合中的所有元素）。要实现一个集合类型，首先可以使用简单的数组，但是数组元素查询的时间复杂度是O(n)；比数组好得多的另一个选择是二叉搜索树，它本身就提供了上述的三个操作，而且速度都很快：O(logn)，这种实现一般称为TreeSet。二叉搜索树在操作的时候需要维护元素之间的相对顺序，而集合对顺序是没有要求的，是否可以提供更好的时间复杂度呢？

答案就是HashSet，相关的方法是散列法（Hashing），这也是本文的主要内容。关于集合更详细的讨论（泛型接口ISet<T>，集合之间的操作，如交集、并集等）将在下篇中进行。

散列法

现在再来明确一下目标。我们要实现的Set类要满足元素的互异性，但不关心元素的顺序如何；要支持的操作是添加(insert)元素、移除(remove)元素、查询(find)（判断某个值是否在集合中）；每种操作的时间复杂度要比O(logn)好。

对于数组来说，如果知道了下标，那么访问该元素的时间复杂度为O(1)，现在看能否利用这一点。考虑一种简单情况，我们要处理的集合包含若干小的整数，范围在0到99之间，并且事先可以确定集合的元素个数不会超过100。此时，可以创建一个长度为100的int数组a，其元素全部初始化为0。对于一个数i，要完成insert(i)操作，只要执行a[i] = 1；对于remove(i)操作，只需要a[i] = 0；find(i)操作，可以返回a[i] == 1（或a[i] > 0）。

三种操作的时间复杂度都是O(1)，实现起来也很简单，看起来不错。不过它有两个明显的问题，如果要保存的整数不是一个小范围内的值，而是所有int，那么数组a的长度要超过40亿，太不现实；另外，我们要实现的是泛型类，可以容纳各种类型的值，如果不是int，而是string，元素本身的值不能用作索引。

上面的两个问题也是散列法的两个核心问题。先来看第二个问题：对于非整型的值，如何获得它对应的数组下标。以string为例，假设它包含的字符都是ASCII字符，对应的int值范围是0-127。对于“junk”，可以这样来计算：'j'*128^3 + 'u'*128^2 + 'n'*128^1 + 'k'*128^0，这样就把一个string值转换为int值了。不过这种方法会产生巨大的整数，对于“junk”这样简单的字符串，产生的值就高达224229227，可以想见，对于复杂一点儿的字符串将是不能接受的。于是又回到了上段中的第一个问题，如何避免使用过于巨大的数组？

如果集合的元素是int类型，虽然int的可能值超过40亿，但是在一个特定的问题中，集合的元素个数却可能很有限。如果元素个数不超过1000，那么只需要一个长度为1000的数组就够了，如果一个值超过了数组下标的上限，可以通过一个函数将该值映射到0-999，这样的函数称为散列函数（hash function）。

散列函数

根据上面的分析，对于一个集合S，用来存放元素的数组长度为tableSize，其中的任一元素e，散列函数h将e映射到0到tableSize之间的一个整数（即数组的一个有效索引），可以记为：

index = h(e, tableSize)

首先针对元素e，根据某种特定的方法计算出它的int值hashCode，然后返回hashCode % tableSize，这样返回值就会落在0到tableSize-1之间。显然，在散列函数的实现中，最重要的部分就是计算hashCode。你也许已经想到了一个方法，那就是object.GetHashCode()，这里需要的正是它。该方法是virtual的，这样它的每个子类都可以提供自己的实现。比如下面的例子：

（图片来自wikipedia，将string类型的值映射到tableSize为16的数组上。）

前面提到过，很多情况下，元素e的取值范围要比tableSize大得多，这样就有可能遇到一种情况，对于不同的两个元素e1和e2，有h(e1, tableSize) == h(e2, tableSize)，此时它们被映射到同一个数组索引，这种复杂的情况称为冲突（collision），在本文后面会讨论如何解决冲突问题。

一般地，一个好的散列函数需要满足：

• 容易计算（主要是指散列函数的时间复杂度为常数时间）。
• 将元素均匀地映射到数组中，减少冲突的可能；

如果元素类型是基元类型，可以使用它们内置的GetHashCode实现，对于自定义类型的实现，将会在下篇中进行讨论。

当冲突发生时

现在我们已经有了散列函数，接下来需要确定当冲突发生时如何化解它。具体来说，如果一个元素e，经过散列函数求值，被散列到的位置已经被另一个元素占据，那么e应该放在哪里？

最简单的方法是，下一个位置。在数组中顺序搜索，直到找到一个空位置。为利用数组的所有空位置，搜索进行到数组尾部时，可以绕回到第一个位置。这种方法就是线性探测法（linear probing）。

考虑一个例子，数组长度tableSize = 10，要添加的元素是89、18、49、58和9。散列函数的返回结果为：

hash(89, 10) → 9
hash(18, 10) → 8
hash(49, 10) → 9
hash(58, 10) → 8
hash(9, 10) → 9

索引	insert(89)	insert(18)	insert(49)	insert(58)	insert(9)
0			49	49	49
1				58	58
2					9
3
4
5
6
7
8		18	18	18	18
9	89	89	89	89	89

在添加89和18时，没有冲突。添加49时，与89冲突，寻找下一个空位置，由于到达数组尾部，绕回，在索引0处存放49；接下来的58和9与此类似。只要数组足够大，就可以找到一个空位置。但问题是，“探测”的时间可能会很长，如果只有一个空位置，那么要搜遍整个数组才能找到，平均下来要搜索半个数组，这与我们的每个操作都是常数时间的期望已经相去甚远了。

再来看find操作，它的探测路径与insert相同。要找58，从索引8（hash的返回值）开始，这个位置有一个元素，但不是58；继续向下看索引9，仍然不是，直到索引1，找到了匹配的元素。要找19，从索引9开始，历经9、0、1、2，最后到了一个空位置3，这说明数组中没有与之匹配的项。

最后是remove操作，不能直接将元素删除（将该位置置空）。从上面分析可以看到，insert和find操作都需要一条探测路径，如果直接删除，就会打断这条路径，从而使find操作失效。如果把89直接删除，那么49、58和9就都找不到了。

线性探测法的简单分析

在上面的例子中，向空的数组添加元素时没有冲突，到后来冲突越来越多，这也是符合我们的直觉的。公交车上越拥挤，冲突发生的可能性就越大。在散列法中有一个专门的术语：负载因子（load factor）。探测散列表的负载因子λ是表被装满的比例，范围从0（空）到1（满）。

使用线性探测法时，比较容易产生连续被占据的块，如果一个元素被散列到这个块中，就需要连续尝试以找到下一个可用位置（看上面添加9时）。这种连续聚集的块称为初始聚集（primary clustering）。用线性探测法添加项时，需要尝试的平均单元数大约是 。

如果λ=0.5，尝试次数为2.5，还是可以的；如果λ=0.9，那么尝试次数就多达50次了（这还是平均数，某些情况比这更糟）。

对于find操作来说，可以分为两种情况：不成功的和成功的。不成功的情况与insert操作一样。如果查找成功，需要检查的平均单元数约为 。

如果λ=0.5，尝试次数为1.5；如果λ=0.9，尝试次数为5.5。

看来λ=0.5是个不错的选择，平均探测次数很少，也不会需要大量的空闲位置，而且很容易实现。不过，为了减少探测数，我们需要一种能避免初始聚集的方法，一种选择就是二次探测法。

二次探测法（quadratic probing）

在线性探测法中，当发现冲突产生时，我们会从冲突位置开始顺序探测下一个可用位置，这正是产生初始聚集的原因。如果散列函数hash的返回值为h，那么探测的位置将依次是h + 1，h + 2，...，h + i。探测的位置连续，当然就容易产生聚集了。既然这样，就不要探测连续的位置了，记为 ，现在改为依次探测h + f(1)，h + f(2)，...，h + f(i)。下面来看二次探测法的使用，还是使用前面的那个例子。

hash(89, 10) → 9
hash(18, 10) → 8
hash(49, 10) → 9
hash(58, 10) → 8
hash(9, 10) → 9

索引	insert(89)	insert(18)	insert(49)	insert(58)	insert(9)
0			49	49	49
1
2				58	58
3					9
4
5
6
7
8		18	18	18	18
9	89	89	89	89	89

在添加49时，与89冲突，49的最终位置是(9 + 1) % 10 = 0；添加58时，与18冲突，而(8 + 1)位置与89冲突，所以58的最终位置是(8 + 2^2) % 10 = 2；同理，9的位置是3。这里有个相当重要的地方是，hash值为8的元素和hash值为9的元素探测路径不同，添加58不会影响到后面添加9，这是比线性探测好的地方。

在编码之前，我们再来考虑几个问题，这几个问题解决后，你会发现二次探测法的实现灰常简单。这几个问题是：

1. 使用线性探测法，虽然它可能会比较慢，但它可以保证的是，只要数组不满，就可以插入新的值，二次探测法也可以做到这一点吗？另外，探测路径中的位置会不会被重复探测到？

2. 线性探测法实现只需要简单的计算，二次探测法则需要乘法和模运算，这会不会造成太大的负担？

3. 如果λ过高怎么办？能否动态扩展数组？

对于问题1，如果tableSize为素数，而且λ不超过0.5，就可以解决，即下面的定理：

定理1：如果采用二次探测法并且表（数组）的大小是素数，表至少有一半是空的（即λ <= 0.5），那么新的元素总能插入，插入过程中没有一个位置会被探测两次。

证明：设表的大小为M，M为大于3的奇素数。现在考虑探测序列的前 项（包括初始项），可以证明它们彼此是不同的。这里使用反证法。假设这些项的某两个项是和，其中 。若这两项相同且 ，那么

因为M是素数，所以i-j或i+j可以被M整除，因为i和j不同且它们的和小于M，这两种情况都不可能。可以得出，这两项是不同的，由于λ>0.5（M为奇数），所以这项中必然有一项是空位置，这样元素总能插入，且不会有位置被探测两次。

对于问题2，线性探测法需要的计算需要一次简单的加法（加1）、一个确定是否需要绕回表头的测试，一个很少出现的减法（返回表头）。二次探测法需要做一次加法（i – 1到i）、一次乘法（i * i）、一次加法和一次取模，看起来开销很大。通过下面的定理：

定理2：不需要昂贵的乘法和取模就能实现二次探测法。

简单说一下证明。探测序列中的相邻两项是 和 ，那么 。

问题3的出现是因为，要解决问题1，我们需要保证λ不超过0.5，随着元素的增加，需要动态扩展数组，这个过程称为重散列（rehashing）。扩展为新的数组后，不能简单的将元素拷贝过去，因为新的tableSize意味着新的散列函数，这里的做法是重新检查原有数组的每个元素，将它们添加到新数组中。

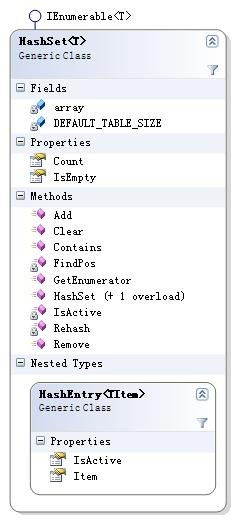
现在可以来考虑HashSet的具体实现了，首先来看HashSet的Hash部分，通过散列法实现Set的三种基本操作。HashSet的类图大致如下：

这里通过嵌套类HashEntry来存放集合中的值，前面提到过，不能够直接删除某个项，而是通过一个IsActive属性进行标识。对于主要的三个操作Add（insert）、Remove和Contains（find）来说，它们都需要一个探测序列来找到insert的位置或是查询是否包含某个值。这个类似的探测过程都放在了FindPos方法中：

private int FindPos(T item)
{
    int collisionNum = 0;
    int pos = (item.IsNull()) ? 0 : Math.Abs(item.GetHashCode() % array.Length);

    while (array[pos].IsNotNull())
    {
        if (item.IsNull())
        {
            if (array[pos].Item.IsNull())
            {
                break;
            }
        }
        else if (item.Equals(array[pos].Item))
        {
            break;
        }

        pos += 2 * (++collisionNum) - 1;
        if (pos >= array.Length)
        {
            pos -= array.Length;
        }
    }

    return pos;
}

第4行获得初始散列值，第20行使用的是定理2中的公式。

有了FindPos方法，三个操作的代码都变得简单了：

public bool Add(T item)
{
    int pos = FindPos(item);
    if (IsActive(pos))
    {
        // Item exists, just return.
        return false;
    }

    array[pos] = new HashEntry<T>(item, true);
    currentSize++;
    occupied++;
    modCount++;

    if (occupied > array.Length / 2)
    {
        Rehash();
    }

    return true;
}

public bool Remove(T item)
{
    int pos = FindPos(item);
    if (!IsActive(pos))
    {
        return false;
    }

    array[pos].IsActive = false;
    currentSize--;
    modCount++;

    if (currentSize < array.Length / 8)
    {
        Rehash();
    }

    return true;
}

public bool Contains(T item)
{
    return IsActive(FindPos(item));
}

private bool IsActive(int pos)
{
    return array[pos].IsNotNull() && array[pos].IsActive;
}

另外几个需要注意的地方是，默认的tableSize = DEFAULT_TABLE_SIZE = 101，二次探测法要求tableSize为素数。在需要Rehash（扩展和收缩）的时候，也需要保持tableSize为素数。完整的代码在这里(IsNull和IsNotNull只是两个简单的扩展方法，判断某个变量是否为null)。

到这里，我们使用二次探测法实现了HashSet的三个基本操作，不过关于GetHashCode方法和ISet接口的实现，这里还没有提及，这些留在下一篇中进行讨论。

其它冲突解决方法

还有一种流行的方法是分离链接法（separate chaining）：

（图片来自wikipedia）

如上图，John Smith和Sandra Dee都散列到了152位置，它们对应的两个值将形成一个链表，也就是它们被放在了同一个桶（bucket）里，这样的好处是不会大量的“空桶”，从而节省了空间。理解了二次探测法，这个也比较容易理解。

小结

本文主要讨论了散列法和散列函数的基本概念以及解决散列冲突的两种方法：线性探测法和二次探测法，并以二次探测法简单地实现了HashSet的Hash这一部分。在下篇中将会讨论GetHashCode方法在自定义类型中的实现以及给HashSet添加对ISet接口的实现，那样才算是一个真正的Set。

参考

《数据结构与问题求解》
Hash Function
Hash Table