标注随测量物体旋转问题

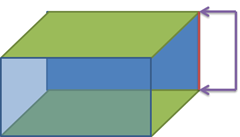
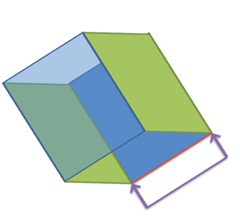
假设我们对如下Block中的红色线段做了标注，那么这个标注的两个锚点(Anchor Point)分别为红色线段的2个端点

当我们旋转这个Block后，我们自然希望这个标注也跟着物体旋转的，调整到如下合理的位置，  

现在的问题是如何为这个标注求得变换矩阵。

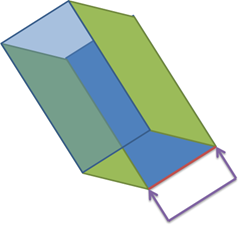
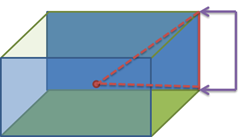
一开始我以为只要根据红色初始位置，跟终止位置，求得它的变换矩阵，再作用到标注上就可以了。 但是结果下来，发现自己想简单了。在上面第二张图中，用户可以继续绕着红色线段，旋转Block，比如得到下面的形状：

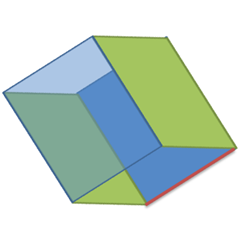
我们发现实际上第二张图跟第三张图中红色线段对应的向量是一样的,那么计算出来的变换矩阵肯定跟第二张图一样，得到的一定是下面这个错误的结果：

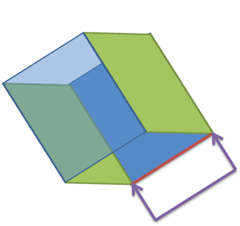
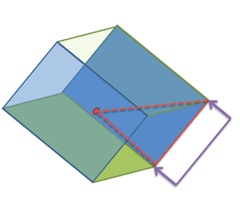
正确的结果应该如下：

这个问题的本质原因在于： 一条直线不能决定平面。 那么2点不能决定平面，三点总归可以了吧。关键问题就是第三个点怎么选取。这个第三个点必须相对红色线段是稳定的，那么当Block旋转后，我们依然能够找回来。于是想到了求这个Block的中心点，而后构建一个平面，根据这个平面前后位置，求得变化矩阵，问题就得以解决了。

 

原始矩阵：

Vector3d vecX =  (p2 - p1).Normal();
Vector3d refVec = (centerPoint - p1).Mormal();
Vector3d vecZ = vecX.CrossProduct(refVec);
Vector3d vecY = vecX.CrossProduct(vecZ);
Matrix3d m0 = new Matrix3d();
m0.SetCoordinateSystem(p1, vecX, vecY, vecZ); // orignal transform

新的矩阵：

Vector3d vecX' = (p2' - p1').Normal();
Vector3d refVec' = (centerPoint' - p1').Mormal();
Vector3d vecZ' = vecX'.CrossProduct(refVec');
Vector3d vecY' = vecX'.CrossProduct(vecZ');
Matrix3d m1 = new Matrix3d();
m1.SetCoordinateSystem(p1', vecX', vecY', vecZ'); // new transform

变换矩阵：

Matrix3d transform = m1 * (m0.Invert());