黄河小浪底调水调沙问题
黄河小浪底调水调沙问题
问题提出
2004 年 6 月至 7 月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功。整个试验期为20多天，小浪底从6月19日开始预泄洪放水，直到7月13日结束并回复成功供水。小浪底水利工程按设计拦沙量为 75.5 亿\(m^3\)，在这之前，小浪底共积沙达 14.15 亿 t。表 5.8 是由小浪底观测站从 6 月 29 日到 7 月 10 日检测到的试验数据。
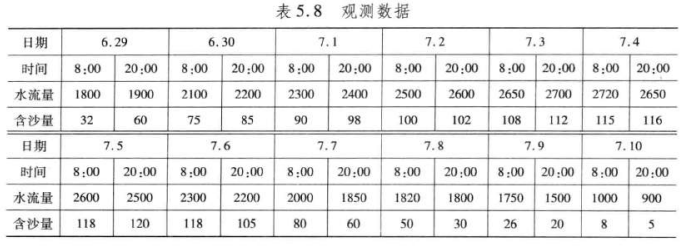
根据试验数据建立数学模型研究下面的问题：
(1) 给出估计任意时刻的排沙量及总排沙量的方法。
(2) 确定排沙量与水流量的关系。
模型的建立与求解
已知给定的观测时刻是等间距的，以 6 月 29 日零时刻开始计时，则各次观测时刻（离开始时刻 6 月 29 日零时刻的时间）分别为：
计时单位为 s。
第一次观测的时刻 \(t_1=28800\)，最后一次观测的时刻 \(t_{24}=1022400\)。
记第 i (i=1,2,...,24) 次观测时水流量为 \(v_i\)，含沙量为 \(c_i\)，则第 \(i\) 次观测时的排沙量为 \(y_i=c_iv_i\)，有关的数据见表5.9。
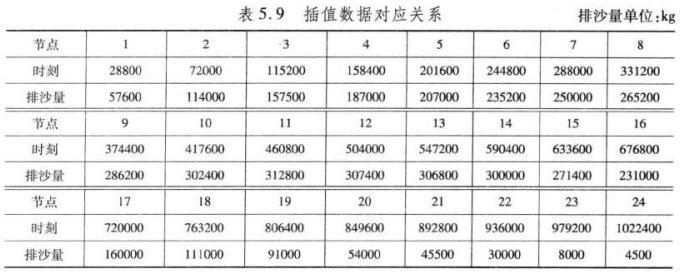
对于问题(1)，根据所给问题的试验数据，要计算任意时刻的排沙量，就要确定处排沙量随时间变化的规律，可以通过插值来实现，考虑到实际中的排沙量为时间的连续函数，为了提高模型的精度，采用三次样条函数进行插值。
利用 Matlab 函数，求出三次样条函数，得到排沙量 \(y=y(t)\) 与时间的关系，然后进行积分，就可以得到总的排沙量：
计算的 Matlab 程序如下：
load data3.txt %将表 5.8 中的日期和时间数据行删除，余下的数据保存再纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:);
sha=data3([2,4],:); sha=sha'; sha=sha(:);
y=sha.*liu; y=y'; %计算排沙量，转变成行向量
i=1:24;
t=(12*i-4)*3600;
t1=t(1); t2=t(end);
pp=csape(t,y); % 进行三次样条插值
xsh=pp.coefs %求得插值多项式的系数矩阵，每一行是一个区间上多项式的系数
TL=quadl(@(tt)fnval(pp,tt),t1,t2) % 求含沙总量的积分运算
对于问题 2，研究排沙量与水流量的关系，从试验数据可以看出，开始排砂量是随着水流量的增加而增长，而后是随着水流量的减少而减少。显然，变化规律并非是线性的关系，为此，把问题分成两部分，从开始水流量增加到最大值 2720 \(m^3/s\) 为第一阶段，从水流量的最大值到结束为第二阶段，分别来研究水流量与排沙量的关系。
画出排沙量与水流量的散点图：
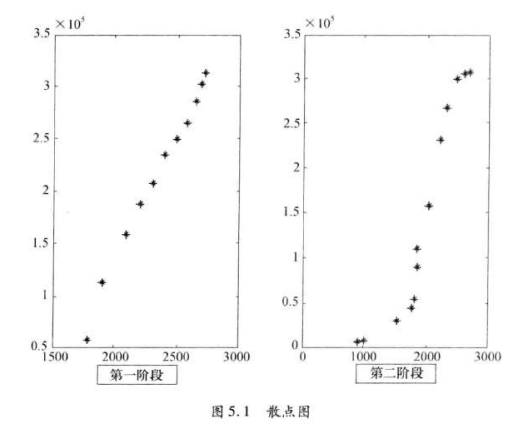
画散点图的程序如下：
clc,clear
load data3.txt %将表 5.8 中的日期和时间数据行删除，余下的数据保存再纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:);
sha=data3([2,4],:); sha=sha'; sha=sha(:);
y=sha.*liu;
subplot(1,2,1),plot(liu(1:11),y(1:11),'*')
subplot(1,2,2),plot(liu(12:24),y(12:24),'*')
从散点图可以看出，第一阶段基本是线性关系，第一阶段和第二阶段都准备用一次和二次曲线来拟合，哪一个模型的剩余标准差小就选用哪个模型。最后求得第一阶段排沙量 \(y\) 和水流量 \(v\) 之间的预测模型为：
而第二阶段的预测模型为一个二次多项式，即
计算的 Matlab 程序如下：
clc,clear
load data3.txt %将表 5.8 中的日期和时间数据行删除，余下的数据保存再纯文本文件
liu=data3([1,3],:); liu=liu'; liu=liu(:);
sha=data3([2,4],:); sha=sha'; sha=sha(:);
y=sha.*liu;
format long e
% 第一阶段拟合
for j=1:2
nihe1{j}=polyfit(liu(1:11),y(1:11),j);
yhat1{j}=polyval(nihe1{j},liu(1:11);
%求误差平方和与剩余标准差
cha1(j)=sum((y(1:11)-yhat1{j}).^2); rsme1(j)=sqrt(cha1(j)/(10-j));
end
celldisp(nihe1)
rmse1
for j=1:2
nihe2{j}=polyfit(liu(12:24),y(12:24),(j+1));
yhat2{j}=polyval(nihe2{j},liu(12:24));
rmse2(j)=sqrt(sum((y(12:24)-yhat2{j}).^2)/(11-j)); % 求剩余标准差
rmse2
format
