1 为何需要标准化
有的数据,不同维度的数量级差别较大,导致有的维度会主导整个分析过程。如下图所示:
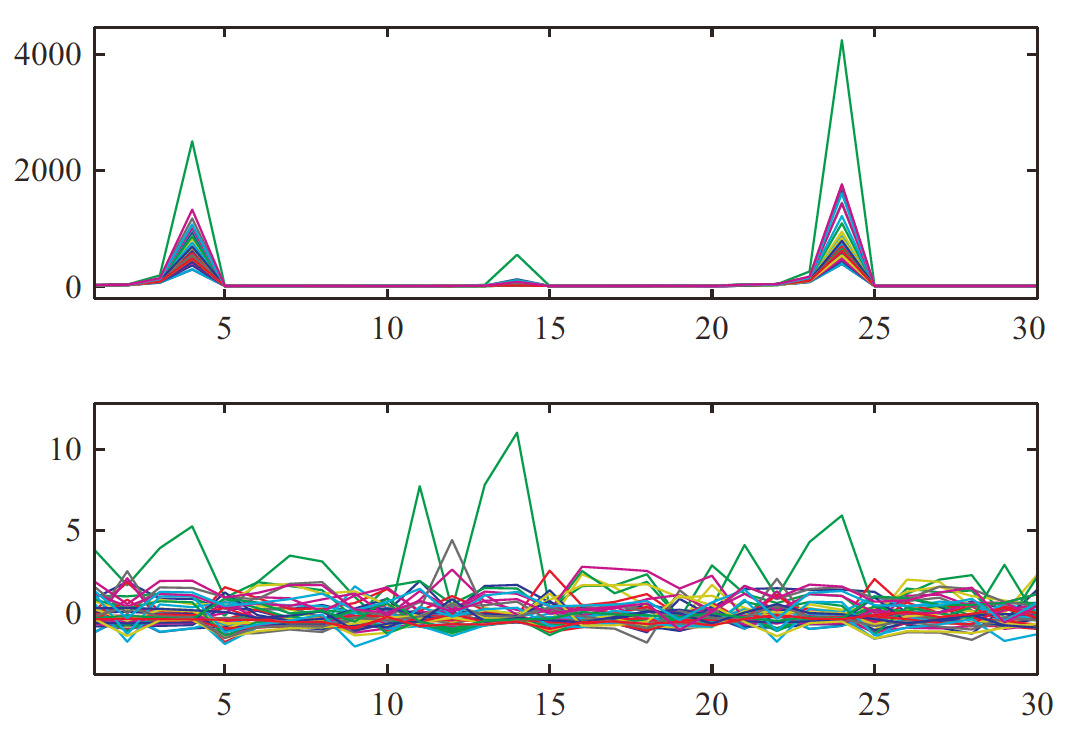
该图的数据维度\(d=30\),样本量\(n=40\),上面的图是对原始数据做PCA后,第一个PC在各个维度上的权重的平行坐标图,下面的图则是对数据做标准化之后的情况。可以发现,在原始数据中,第\(4\)和\(24\)个维度的权重非常大。如果其他的维度也包含了重要的信息,而我们只取第一个PC做研究,可能就会造成信息损失。
2 如何标准化
那该如何预处理数据?一般而言有两种处理方法。
2.1 Scale
常见的一种方法就是对数据做scale,如我们知道数据的总体为\(x\sim (\mu,\Sigma)\),那么可以将\(\Sigma\)的对角线元素单独取出做成一个对角矩阵\(\Sigma_\text{diag}\),然后定义
这样做的好处显而易见,在做完scale后,我们有
这里的\(R\)就是\(x\)的各维度的相关系数矩阵。
对于样本数据\(X\sim \text{Sample}(\bar x, S)\)来说,也可做同样的处理:
同样地,在经过scale后,样本数据的协方差矩阵也变成了相关系数矩阵\(R_S=S_\text{diag}^{-1/2}SS_\text{diag}^{-1/2}\)。
2.2 Sphere
另一种预处理数据的方法是将数据“球形化”(sphere)。即对于总体数据\(x\),可以做
对于样本数据\(X\),也同样可以做
这样做会有什么效果?显然,处理后的协方差矩阵会变为
即我们把各维度之间的相关性也处理掉了。
如果\(\text{rank}(\Sigma)=r\lt d\),\(\Sigma^{-1/2}\)就不存在,此时可以用
对于样本数据也类似。
3 何时需要标准化?
对于这个问题,没有定论。因为数据标准化不影响理论结果。一般来说,如果各个维度是可比的,就不需要标准化,如果不可比,并且我们对量级非常大的数据没有特别的研究偏好,那就需要做标准化。
参考文献
- Koch, Inge. Analysis of multivariate and high-dimensional data. Cambridge University Press, 2013.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号