接触过资产定价的同学可能知道，资产定价有一个核心公式\(p=\text{E}(mx)\)，它的内涵十分丰富。本文将从Consumption-based model出发，详解该公式的由来，并以它为视角，介绍金融理论中的一些问题。

1 定价方程

1.1 基本的定价方程

假设有一笔在\(t+1\)时刻的payoff为\(x_{t+1}\)的资产，该如何计算它在\(t\)时刻的价值？

假如在今天买一只股票，那么下一期的payoff就是股票的价格加股息，即\(x_{t+1}=p_{t+1}+d_{t+1}\)，\(x_{t+1}\)是一个随机变量，投资者无法确切地知道他的投资在下一期会有多少收益，但他可以估算各种可能情况的概率。假设有一个代表性投资者，他的效用函数是

\[U(c_{t},c_{t+1})=u(c_t)+\beta \text{E}_t[u(c_{t+1})] \]

其中\(c_t\)表示在\(t\)期的消费。假设效用函数是幂效用函数

\[u(c_t)=\dfrac{1}{1-\gamma}c_t^{1-\gamma} \]

当\(\gamma\to 1\)时，\(u(c)=\ln(c)\)。\(\beta\)是主观贴现因子（subjective discount factor），效用函数的曲率表示对风险和跨期替代的厌恶程度。

假设投资者可以以\(p_t\)的价格自由买卖任意数量的资产\(x_{t+1}\)，初始消费水平为\(e\)，他选择买入\(\xi\)数量的资产，那么可列出方程：

\[\begin{aligned} \max_{\{\xi\}} u(c_t)&+\text{E}_t[\beta u(c_{t+1})] \\ \text{s.t.} \quad c_t&=e_t-p_t\xi,\\ c_{t+1}&=e_{t+1}+x_{t+1}\xi \end{aligned} \]

将约束条件代入后求解最值问题，解得：

\[p_t u'(c_t)=\text{E}_t\left[\beta u'(c_{t+1})x_{t+1}\right] \]

上式可写为：

\[p_t=\text{E}_t\left[\beta \dfrac{u'(c_{t+1})}{u'(c_t)}x_{t+1}\right] \tag{1} \]

1.2 边际替代率与随机贴现因子

定义随机贴现因子（Stochastic Discount Factor，SDF）

\[m_{t+1}=\beta \dfrac{u'(c_{t+1})}{u'(c_t)} \]

代入\((1)\)式可得\(p_t=\text{E}_t(m_{t+1}x_{t+1})\)。这里的\(m_{t+1}\)可以叫作边际替代率（marginal rate of substitution），也叫定价核（pricing kernel），或者测度变换（change of measure）、状态价格密度（state-price density）等。在大多数时候，下标可以省略，条件期望和无条件期望也没必要区分，可以写作\(p=\text{E}(mx)\)。

如果不存在不确定因素，那么按照标准现值公式，应该有

\[p_t=\dfrac{1}{R_f} x_{t+1} \]

其中\(R_f\)为毛无风险利率（gross risk-free rate），\(1/R_f\)为贴现因子。用大写的\(R\)表示毛收益率，小写的\(r\)表示净收益率，关系是\(r=R-1\)或\(r=\ln(R)\)。

对于payoff相同的风险资产，风险越大，价格越低，因此风险资产的定价可用风险调整的贴现因子（risk-adjusted discount factors），它和某个资产有关：

\[p_t^i = \dfrac{1}{R^i} \text{E}(x_{t+1}^i) \]

2 金融中的经典问题

本节以\(p=\text{E}(mx)\)为视角，来看一些金融中的经典问题。

2.1 无风险利率

现在研究无风险债券，它的payoff就是无风险利率\(R^f\)，它在\(t\)期的价格为\(1\)，因此有\(1=\text{E}(mR^f)=\text{E}(m)R^f\)，因此，无风险利率为：

\[R^f=\dfrac{1}{\text{E}(m)} \]

若效用函数取为\(u(c_t)=\dfrac{1}{1-\gamma}c_t^{1-\gamma}\)，代入\(m\)的表达式中，并消除不确定性（拿掉期望符号），可得

\[R^f = \dfrac{1}{\beta} \left(\dfrac{c_{t+1}}{c_t}\right)^\gamma \]

可以看出，在排除不确定因素后，无风险利率水平与\(\beta\)、消费增长率、效用函数曲率\(\gamma\)有关。

而如果存在不确定性呢？假设消费增长率是对数正态分布，定义对数无风险利率为\(r_t^f=\ln R^f_t\)，定义主观贴现率\(\delta=-\ln \beta\)，记\(\Delta\ln c_{t+1}=\ln c_{t+1}-\ln c_{t}\)，\(\Delta\)表示一阶差分算子。那么

\[R^f = 1/{\text{E}_t\left[\beta\left(\dfrac{c_{t+1}}{c_t}\right)^{-\gamma}\right]} \]

已知对于正态分布变量\(z\)，有\(\text{E}(e^z)=e^{\text{E}(z)+(1/2)\sigma^2(z)}\)，代入上式后得

\[R^f_t=\left[e^{-\delta} e^{-\gamma \text{E}_t(\Delta\ln c_{t+1})+(\gamma^2/2)\sigma^2_t(\Delta\ln c_{t+1})}\right]^{-1} \]

两边取对数后得：

\[r_t^f=\delta+\gamma\text{E}_t(\Delta\ln c_{t+1})-\dfrac{\gamma^2}{2}\sigma^2_t(\Delta\ln c_{t+1}) \]

可以看到，在存在风险时，无风险利率水平依旧与不耐心程度\(\delta\)、消费增长率、幂参数\(\gamma\)有关。

2.2 风险调整

利用协方差的定义，以及上一节中得出的无风险利率表达式\(R^f=1/\text{E}(m)\)，可以得到

\[\begin{aligned} p&=\text{E}(mx)\\ &=\text{E}(m)\text{E}(x)+\text{Cov}(m,x)\\ &=\dfrac{\text{E}(x)}{R^f}+\text{Cov}(m,x) \end{aligned} \]

这就是标准的贴现现值公式，协方差项就是风险调整（risk adjustment）。

在上式中令资产\(i\)价格为\(1\)，那么payoff\(x\)就成了资产\(i\)的收益率\(R^i\)，可得：

\[\text{E}(R^i)-R^f=-R^f \text{Cov}(m,R^i) \tag{2} \]

2.3 异质性风险不影响价格

在金融理论中，我们知道，在payoff中只有与贴现因子完全相关的成分会带来额外的收益率，与贴现因子无关的异质性风险（idiosyncratic risk）不产生溢价。由上一小节的内容可知，当\(\text{Cov}(m,x)=0\)时，不管\(\sigma^2(x)\)有多大，始终有\(p=\dfrac{\text{E}(x)}{R^f}\)。

将\(x\)对\(m\)做回归，可将它分解为

\[x=\text{proj}(x|m)+\varepsilon \]

其中\(\text{proj}(x|m)\)就是与贴现因子完全相关的部分（systematic risk），残差\(\varepsilon\)是完全无关的异质性风险（idiosyncratic risk）。

若回归没有常数项，那么根据回归的知识，我们知道

\[\text{proj}(x|m) = \dfrac{\text{E}(mx)}{\text{E}(m^2)}m \]

依据定价方程，\(\text{proj}(x|m)\)的价格是

\[p(\text{proj}(x|m))=\text{E}(m\cdot\dfrac{\text{E}(mx)}{\text{E}(m^2)}m)=\text{E}(mx)=p(x) \]

而按照回归的正交条件，我们有\(p(\varepsilon)=\text{E}(m\varepsilon)=0\)，也即\(\varepsilon\)的价格为\(0\)。

2.4 期望收益率的Beta表达式

我们来将\((2)\)式进一步改写为：

\[\begin{aligned} \text{E}(R^i)&=R^f+\left(\dfrac{\text{Cov}(R^i,m)}{\text{Var}(m)}\right)\left(-\dfrac{\text{Var}(m)}{\text{E}(m)}\right)\\ &=R^f+\beta_{i,m}\lambda_m \end{aligned} \]

由回归的知识可知，这里的\(\beta\)就是\(R^i\)对\(m\)的回归系数。这又叫beta定价模型，\(\lambda_m\)是风险的价格，与贴现因子的波动率有关，而\(\beta\)是资产的风险的数量。

2.5 均值-方差前沿

可以再对\((2)\)式进行改写，将协方差用相关系数表示：

\[\text{E}(R^i)=R^f-\rho_{m,R^i}\dfrac{\sigma(m)}{\text{E}(m)}\sigma(R^i) \]

而相关系数必在\([-1,1]\)内，因此有

\[\left\vert\text{E}(R^i)-R^f\right\vert \leq\dfrac{\sigma(m)}{\text{E}(m)}\sigma(R^i) \]

上式给了我们很多关于\(R^i\)的期望和标准差的信息（如下图）：

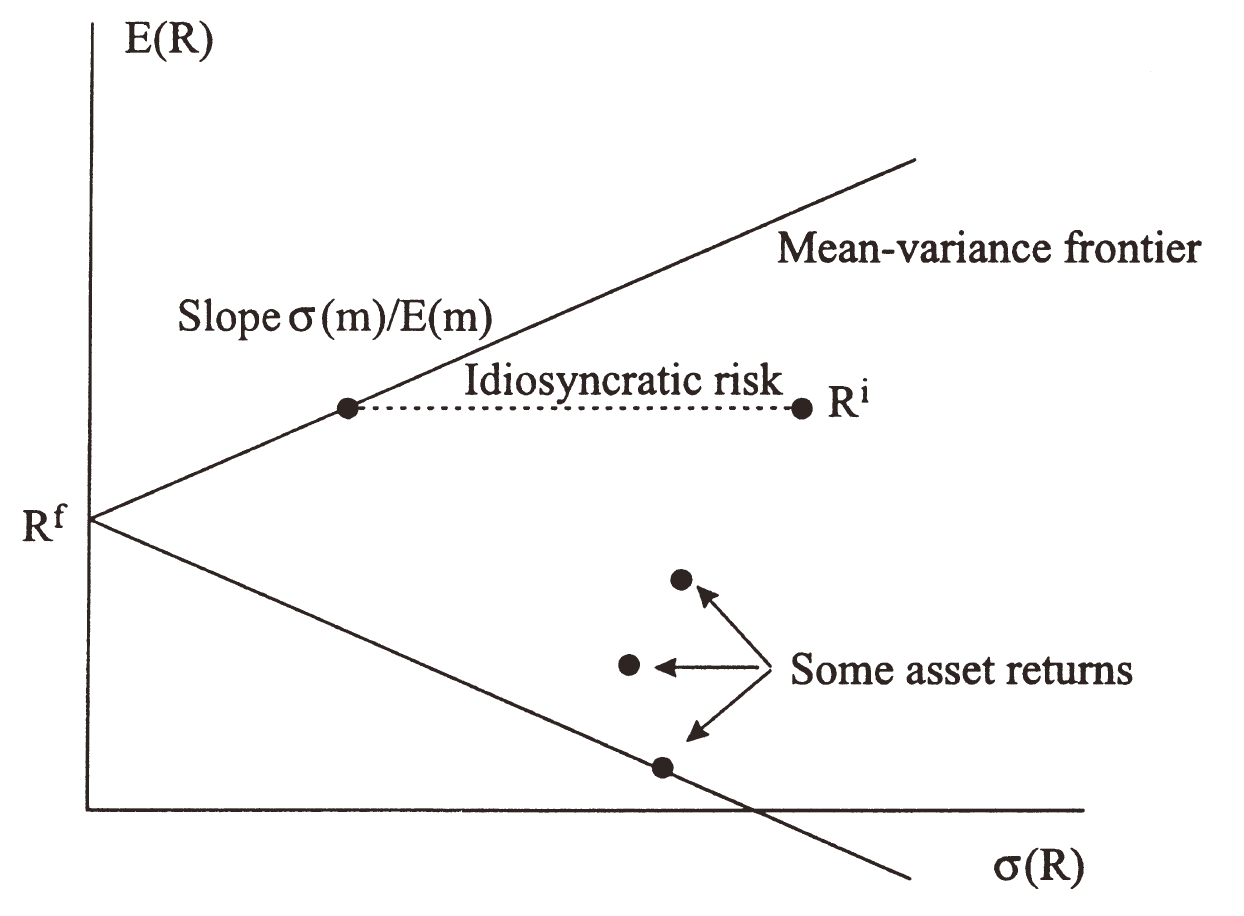
上图说明了：

  • 资产收益率的均值、方差必定落在一个以\(\sigma(m)/\text{E}(m)\)为斜率的楔形区域内，此区域的边界就是均值-方差前沿（mean-variance frontier）；
  • 所有在前沿上的收益率都与贴现因子完全相关即\(\vert\rho_{m,R^i}\vert=1\)。在前沿上部分的资产，收益率与\(m\)完全负相关，反之亦然。
  • 所有在前沿上的收益率相互之间完全相关（因为它们都与\(m\)完全相关）。这一点意味着，只要给出两个在前沿上的收益率，就可以张成（span）（也叫合成，synthesize）任意的前沿收益率，比如给出一个前沿上的资产收益率\(R^m\)，那么所有在前沿上的资产收益率\(R^{mv}\)可以写为\(R^{mv}=R^f+a(R^m-R^f)\)；
  • 给定某个前沿收益率\(R^{mv}\)，它与\(m\)完全相关，那么必有\(m=a+bR^{mv}\)，由此可得\(\text{E}(R^{mv})=R^f-R^f\text{Cov}(m,R^{mv})=R^f-b R^f\text{Var}(R^{mv})\)，那么，beta表达式可改写为

\[\begin{aligned}\text{E}(R^i)&=R^f-R^f\text{Cov}(m,R^i)\\ &= R^f-b R^f\text{Cov}(R^{mv},R^i)\\ &=R^f+ \left(\dfrac{\text{Cov}(R^{mv},R^i)}{\text{Var}(R^{mv})}\right)\left(-b R^f \text{Var}(R^{mv})\right)\\ &=R^f+\beta_{i,mv}\left[\text{E}(R^{mv})-R^f\right]\end{aligned} \]

这个结果很重要，它表明，虽然资产收益率的均值和方差填满了前沿内部的空间，但收益率均值和\(\beta\)之间却是线性关系；

  • 我们可以将收益率分解为priced（或systematic）部分和residual（或idiosyncratic）的部分，如上图所示。

2.6 前沿的斜率和股权溢价之谜

定义超额收益率的均值和标准差之比为夏普比率（Sharpe ratio）：

\[\dfrac{\text{E}(R^i)-R^f}{\sigma(R^i)} \]

而均值-标准差前沿的斜率，就是可获得的最大的夏普比率。利用幂效用函数，并假设消费增长率为对数正态分布，可以得到

\[\begin{aligned} \left\vert\dfrac{\text{E}(R^{mv})-R^f}{\sigma(R^{mv})}\right\vert =& \dfrac{\sigma[(c_{t+1}/c_t)^{-\gamma}]}{\text{E}[(c_{t+1}/c_t)^{-\gamma}]}\\ =& \sqrt{\exp\left[\gamma^2 \sigma^2(\Delta\ln c_{t+1})\right]-1}\\ \approx& \gamma \sigma(\Delta\ln c) \end{aligned} \]

可以看出，经济越带有风险（即增长率波动越大），或投资者风险规避程度越高，那么前沿的斜率就会越大。

理论符合现实吗？不符合！这就是著名的“股权溢价之谜”：在美国数据中，近50年的股票真实收益率均值达到了将近9%，标准差大约是16%，而国库券真实收益率大约是1%，因此，历史Sharpe ratio大约是0.5。但是，总体非耐用品和服务的消费增长率的均值和标准差都是1%左右，根据估算，投资者的风险规避系数达到了50之多！

股权溢价之谜有三种可能性：

  1. 人们的风险规避系数远比学者们计算出来的高；
  2. 过去50年的股票收益都是运气，所以远高于对风险的补偿；
  3. 模型中有地方出错了，比如效用函数或总消费增长率数据。

2.7 随机游走和时变期望收益率

回到由一阶条件导出的\((1)\)式，如果投资者是风险中性的（即\(u(c)\)为线性函数）或消费没有变化，假设payoff中没有股利，即它就是下一期的价格，再假设在短期中\(\beta\)非常接近于\(1\)，那么就有

\[p_t = \text{E}_t(p_{t+1}) \]

这就是鞅（martingale）。它又等价于，价格的时间序列过程形式为：

\[p_{t+1} = p_t+\varepsilon_{t+1} \]

若\(\sigma^2_t(\varepsilon_{t+1})\)为常数，这又叫随机游走（random walk）。

在短期中，鞅的性质表明收益率是无法预测的。但在长期中，情况有所不同：

\[\begin{aligned} \text{E}_t(R_t^f)-R^f =& -\dfrac{\text{Cov}(m_{t+1},R_{t+1})}{\text{E}_t(m_{t+1})}\\ =& -\dfrac{\sigma_t(m_{t+1})}{\text{E}_t(m_{t+1})}\sigma_t(R_{t+1})\rho_t(m_{t+1},R_{t+1})\\ \approx& \gamma_t \sigma_t(\Delta c_{t+1}) \sigma_t(R_{t+1}) \rho_t(m_{t+1},R_{t+1}) \end{aligned} \]

上式表明，长期收益率存在一定的可预测性：

  1. 如果收益率的条件方差\(\sigma_t(R_{t+1})\)是时变的，那么收益率的条件期望也是时变的（会来回穿过代表了Sharpe ratio的直线），但这点对解释没有帮助，因为可以预期方差的变量并不意味着可以预测期望，反之亦然；
  2. 长期收益率的预测可以由变化的风险\(\sigma_t(\Delta c_{t+1})\)或变化的风险厌恶$ \gamma$解释。

2.8 现值表示

如果不用简单的两期模型，而是想将价格和未来所有现金流联系起来，可以考虑投资者的长期目标

\[\text{E}_t \sum_{j=0}^{\infty} \beta^j u(c_{t+j}) \]

同样使用一阶条件，即可得

\[p_t = \text{E}_t \sum_{j=1}^{\infty} \beta^j \dfrac{u'(c_{t+j})}{u'(c_t)}d_{t+j}=\text{E}_t \sum_{j=1}^{\infty} m_{t,t+j} d_{t+j} \]

将上式做\(p_t\)和\(p_{t+1}\)的两期差分，就可以得到两期模型。而如果想反过来，从两期模型推得无限期模型，则需要加一个transversality condition：\(\lim_{j\to \infty} \text{E}_t(m_{t,t+j} p_{t+j})=0\)，它排除了“泡沫”（bubbles）的情况。