在本科阶段的教材中，往往会有多元正态分布的公式出现，但课堂上都不会重点讲解，而在研究生入学考试中也基本不会考。但在实际应用中，多元的情况却非常常见。

本文通过对多元正态分布的公式进行拆解，来正式认识一下它。

1 多元正态分布公式

对于\(D\)维正态分布变量\(x\)，直接上它的密度公式：

\[\mathcal{N}(x|\mu,\Sigma)=\dfrac{1}{(2\pi)^{D/2}}\dfrac{1}{\vert\Sigma\vert^{1/2}}\exp\left\{-\dfrac{1}{2}(x-\mu)'\Sigma^{-1}(x-\mu)\right\} \]

其中\(\mu\)为\(D\times 1\)的均值向量，\(\Sigma\)为\(D\times D\)的协方差矩阵。

公式看起来十分复杂，相信第一次见到时，几乎所有人都会被吓到。沉住气，我们把它拆解了看。

2 公式拆解

先看最后面指数函数中的部分，其中有一个二次型：

\[\Delta^2=(x-\mu)'\Sigma^{-1}(x-\mu) \]

\(\Delta\)叫作\(\mu\)和\(x\)之间的Mahalanobis distance，中文叫马哈拉诺比斯距离或者马氏距离，是印度统计学家Mahalanobis提出的。

\(\Sigma\)一般可以是对称矩阵，考虑它的\(D\)个特征值\(\lambda_i\)和相应的相互正交的特征向量\(u_i\)，\(\Sigma u_i = \lambda_i u_i\)，记\(U=(u_1,\cdots,u_D)\)，\(U\)满足\(U'U=I_D\)，再记\(\Lambda=\text{diag}(\lambda_1,\cdots,\lambda_D)\)，那么可将\(\Sigma\)写成特征向量展开的形式：

\[\Sigma =U\Lambda U'= \sum_{i=1}^{D} \lambda_i u_i u_i' \]

如果做换元\(y=U'(x-\mu)\)，则有\(\Delta^2=y'\Lambda^{-1}y\)，也就是说，通过换元，我们将原来在\(x\)坐标系下的分布，变成了一个在\(y\)坐标系下的、各个分量互相不相关的分布。如图所示：

再看在指数函数前面的部分，由\(\Sigma =U\Lambda U'\)可知\(|\Sigma|=|\Lambda|\)，因此\(|\Sigma|^{-1}=|\Lambda|^{-1}=\prod\limits_{j=1}^{D}\lambda_j^{-1}\)。

利用Jacobian matrix \(J=U'\)，并由\(|J|^2=|U'U|=1\)可得\(|J|=1\)，于是我们可以将原来的密度函数直接变换为

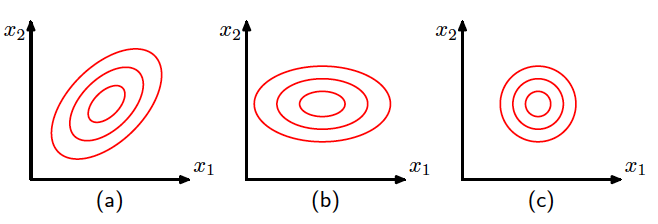
\[\begin{aligned} f_Y(y) =& |J|f_X\left(x(y)\right)\\ =& \dfrac{1}{(2\pi)^{D/2}}\dfrac{1}{\vert\Lambda\vert^{1/2}}\exp\left\{-\dfrac{1}{2}y'\Lambda^{-1}y\right\}\\ =& \prod_{j=1}^{D} \dfrac{1}{(2\pi \lambda_j)^{1/2}}\exp(-\dfrac{y_j^2}{2\lambda_j}) \end{aligned} \]

在原来的\(x\)坐标系下，各分量之间可能有相关性，对应二维时候的图像为下图（1），而在新的\(y\)坐标系下，协方差矩阵变为对角矩阵，也因此图像变为下图中（2）的情况，而若各分量同方差，则会变为类似于标准正态分布的同心圆即下图（3）的形式：