用机器学习预测股票收益率的工作已经屡见不鲜,并有了非常不错的结果,如《当实证资产定价遇上机器学习》。那么,能不能把同样的方法运用到债券中呢?2020年在Review of Financial Studies上的“Bond Risk Premiums with Machine Learning”一文,就使用机器学习方法对债券超额收益率进行了预测。该文作者是伦敦大学玛丽王后学院(Queen Mary, University of London)的Daniele Bianchi、华威大学的Matthias Büchner和罗格斯大学商学院(Rutgers Business School)的 Andrea Tamoni。
1 研究设计
1.1 实验框架
该文做了两个实验:
-
使用收益率曲线数据(即在当前时间的1-10年到期的零息债券的年化到期收益率,共10个),预测某一到期时间的债券在未来一年的超额收益率(即价格涨幅减去无风险利率);
-
在收益率曲线基础上,再用上128个宏观变量,再进行一样的预测。这些宏观变量分为了几组:真实产出和收入,就业和工作时间,零售业、制造业销售数据,国际贸易,消费者支出,住房建造,存货和存货销售率,订单和未履行订单,薪酬和劳动力成本,价格指数,利率和利差,股指,外汇测度。
数据集来自(Liu和Wu,2020)的零息债券收益率曲线。该数据集是日频,构造了每一时间点的1-360个月到期的零息债券的年化到期收益率。
按过去数据的85%和15%划分训练集和验证集(按时间序列顺序),测试集是未来一年的超额收益率。每次测试后,训练集和验证集整体递归地向前扩大一个月,并保持二者比例不变,保持测试集长度为一年。整个数据集时间为1971.08到2018.12(美国的10年到期债券从1971.9开始发行),从1990.1开始进行第一次测试。示意图如下:
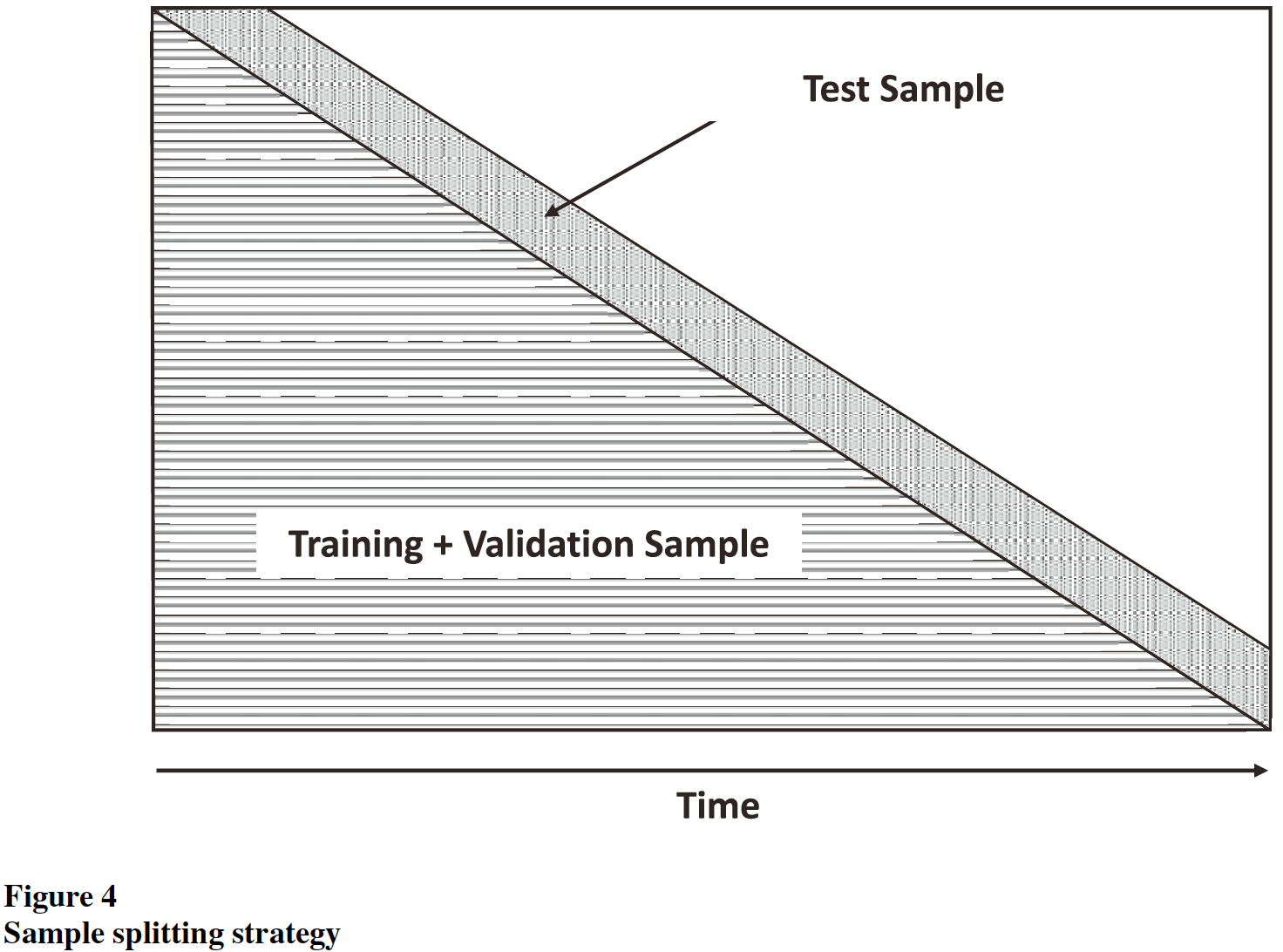
对于每次测试,记录预测的结果,在最后计算样本外\(R^2\):
其中\(xr_{t+1}^{(n)}\)表示\(t+n\)时刻到期的零息债券在从\(t\)时刻到\(t+1\)时刻的超额收益率,\(\mathcal{M}_s\)为使用的机器学习算法。
该文只预测到期为2、3、4、5、7、10年的零息债券,还用这6种债券构造了等权重组合,并预测该组合的\(R^2\)。
检验的原假设为\(R^2<0\),使用MSPE调整后的Clark和West(2007)统计量。
1.2 机器学习算法
这里简单介绍下该文所用的机器学习算法。首先是用了主成分回归和偏最小二乘法,然后还使用了带惩罚项的几种回归方法,即LASSO回归、岭回归、弹性网络。另外,该文还使用了回归树的扩展——梯度提升树(Gradient boosted tree)、随机森林和极限树,如下图:
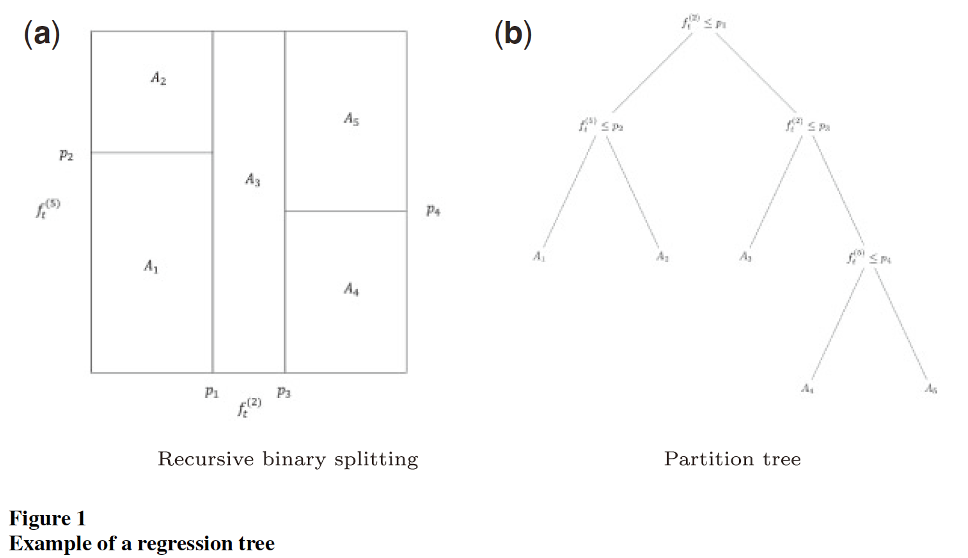
最后,该文使用了一些不同的神经网络结构。当只用收益率曲线数据做预测时,就用经典的前馈神经网络结构,如下图:
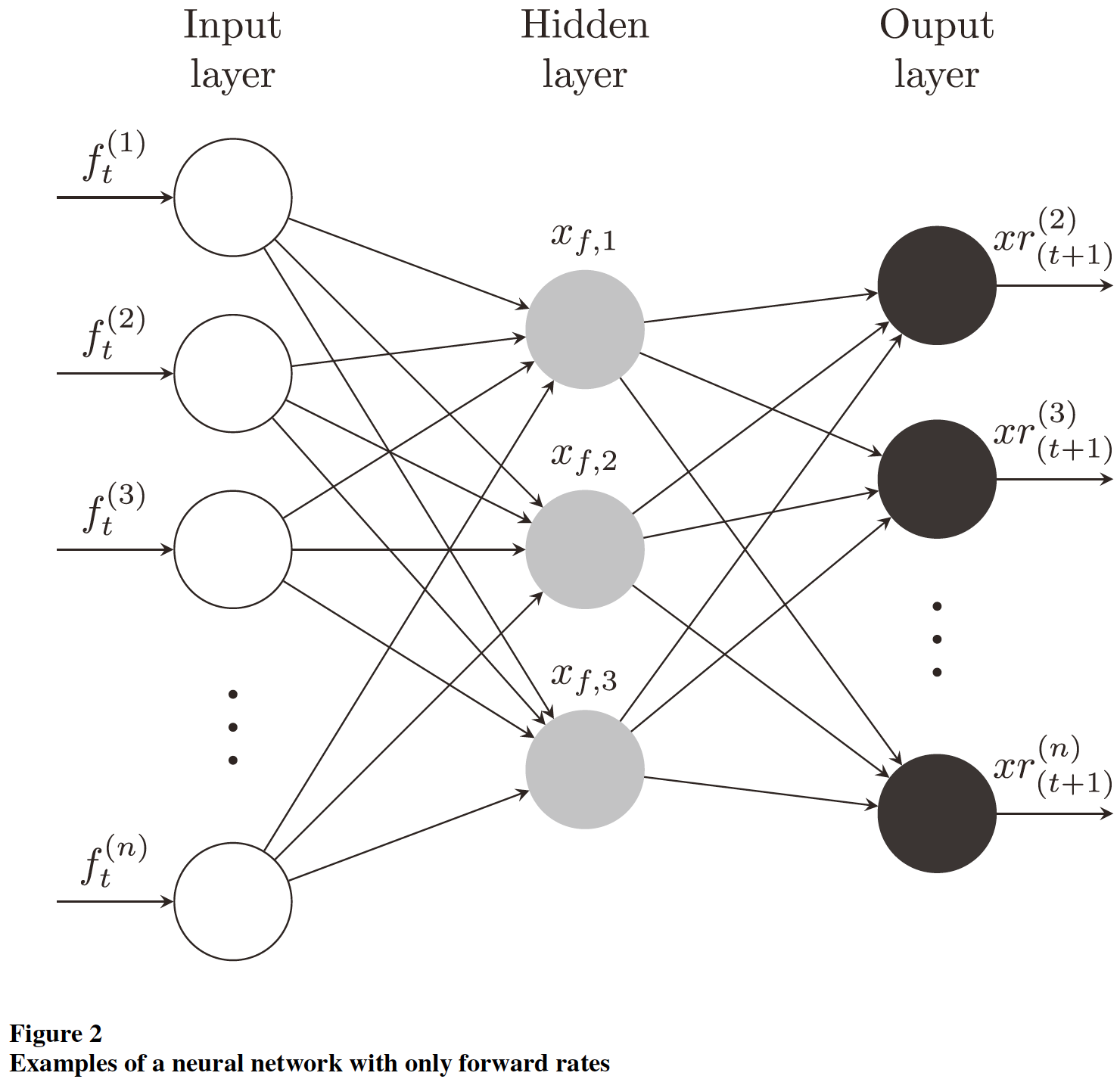
当同时使用收益率曲线数据和宏观数据进行预测时,该文设计了3种不同的网络结构,如下图:

第一种是将利率数据不经过隐含层直接接入输出层(称为hybrid网络),第二种是将两个网络(利率网络和宏观变量网络)联合起来,第三种是在第二种基础上将宏观变量分组集成(称为group ensembling)。
2 实验结果
2.1 只用收益率曲线预测
实验结果如图:
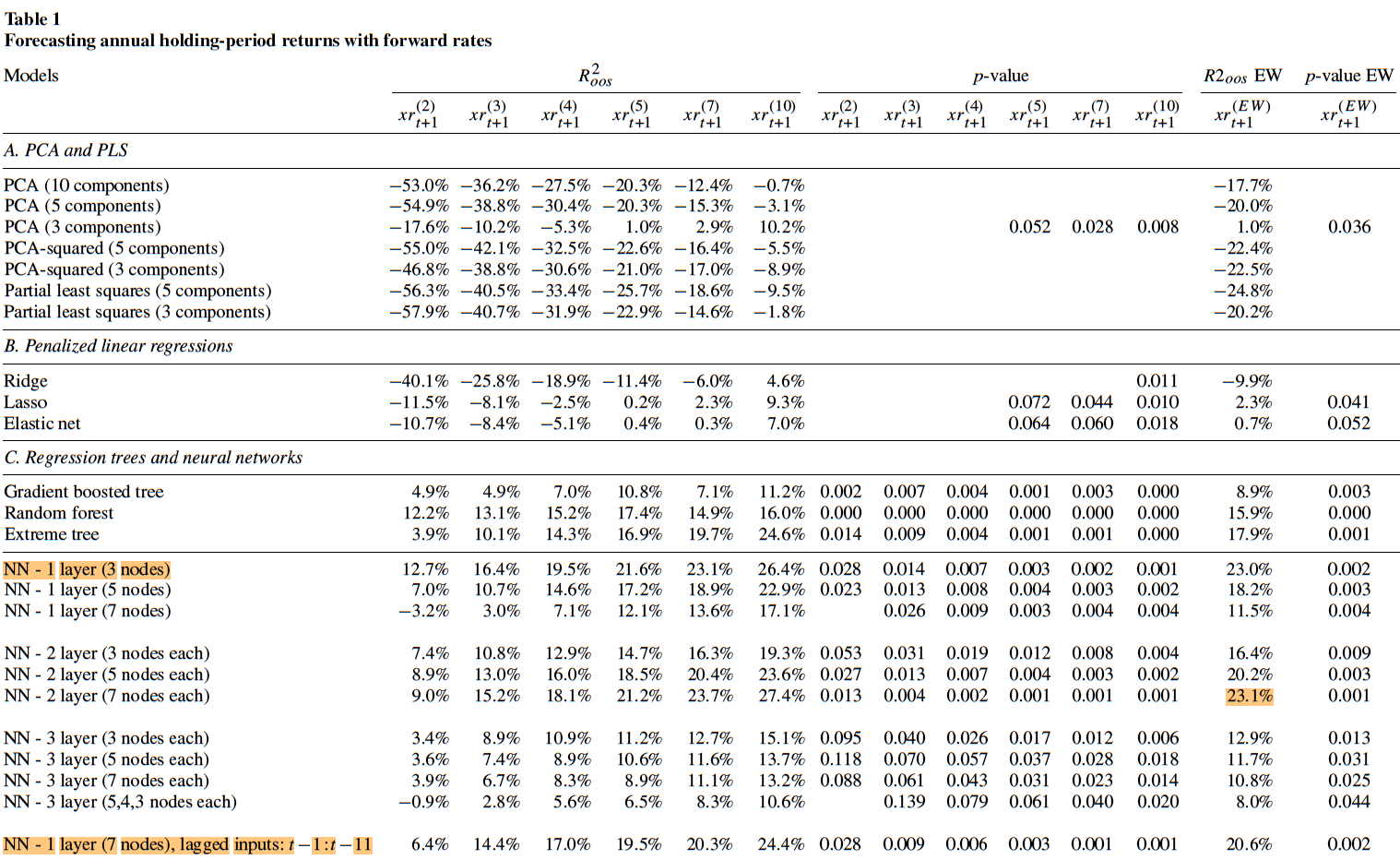
Panel A中,先对收益率曲线取主成分PC,分别取3、5、10个,当用10个主成分时 就是Cochrane和Piazzesi(2005)中的实验。结果\(R^2\)都是负的,用更多PC反而效果更差,再加入非线性项PC的平方后,发现结果更差了。若改用PLS,也无法提高表现。
Panel B中,岭回归\(R^2\)为负,而带有稀疏性的模型(LASSO回归、弹性网络),在预测4年以上到期的债券时\(R^2\)为正,并且预测组合的\(R^2\)也为正。
Panel C中,在一系列树模型中极限树表现最好,可能是因为它有对特征划分位置的随机化。而对于神经网络,浅层网络(1层隐含层,3个结点)表现与深层网络(2层隐含层,7个结点)一样好,再加深网络则会使结果变差;另外,Cochrane和Piazzesi(2005)指出,滞后1-11期的的远期利率包含了远期利率中没有的有关超额收益率的信息,该文将滞后1-11期的的远期利率和10个远期利率一起放入1层隐含层7个结点的网络中,与浅层网络做比较,发现效果没有变好,因此滞后的收益率曲线不能帮助当前时刻的收益率曲线提高预测能力。
2.2 同时用收益率曲线和宏观数据预测
结果如图:

在Panel A和Panel B中,为了与Ludvigson和Ng(2009)可比,第2行是按它的设定,从宏观变量中提取出前8个主成分后再取它的一个子集,而收益率数据上有些(4、5、6行)用了Cochrane和Piazzesi(2005)提取的CP因子 (远期利率的一个线性组合)。结果发现,稠密模型如岭回归或数据压缩,样本外表现很差,稀疏模型则表现较好,并且与2.1中的实验结果相比有明显提高,说明加入宏观变量有助于预测。
Panel C是3种网络的结果,其中混合网络效果拔群,并且加深深度可提高其准确率,而如果用经济学的先验知识选择网络结构,会显著影响预测效果,1层的分组集成网络与3层混合网络效果一样好,并且在7年和10年到期的债券中效果更好。另外,在几种树模型中加入宏观变量后效果也更好,其中极限树效果相对最好。
3 剖析预测性
在经济扩张期和衰退期,可预测性会不会不一样?用NBER的recession indicator划分扩张期和衰退期,分别计算样本外\(R^2\),结果如图:
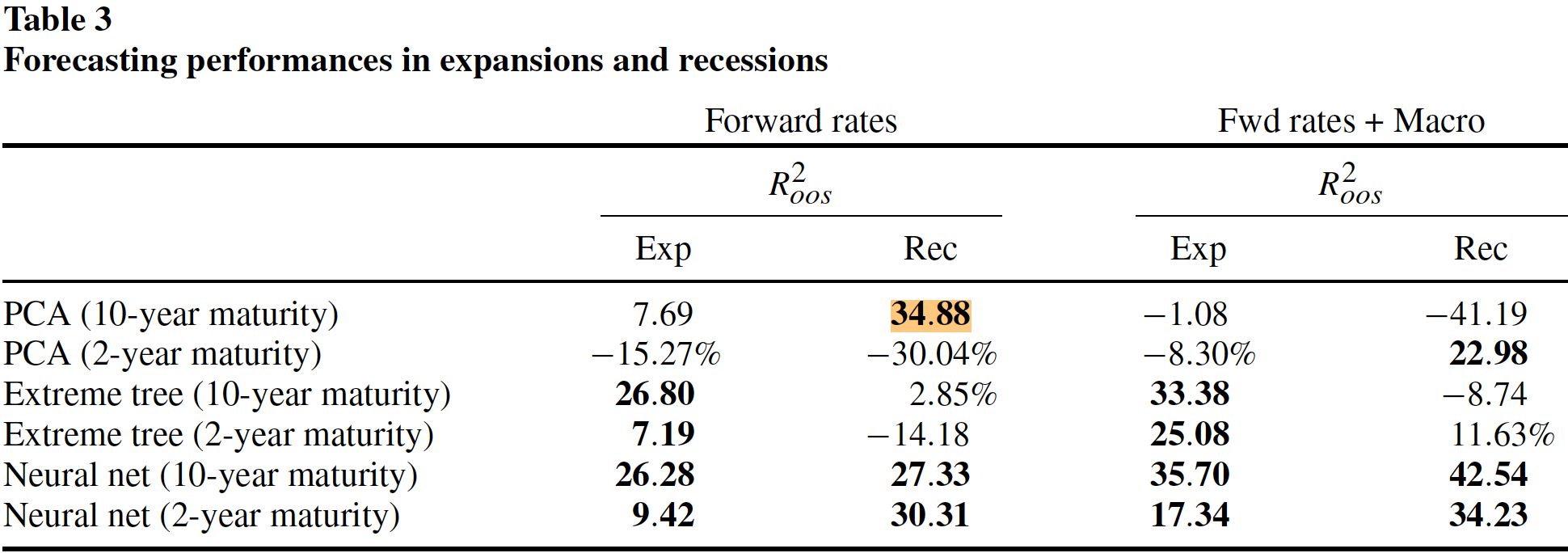
将收益率曲线提取主成分PC,前3个主成分分别代表了收益率曲线的水平(level)、斜率、曲率,可以用回归检验神经网络抽取出的隐含因子对前3个主成分的变动有无预测能力:
其中\(\boldsymbol{x}_t\)为神经网络抽取出的隐含因子,即隐含层的输出。结果如下(第一行为不加入隐含因子,作为参照):

哪些变量重要?可以计算预测值对某个变量的偏微分:
取绝对值后,对所有\(t\)取平均,就得到某个变量的重要性。如果对每组宏观变量的重要性再取平均,就可以得到每组的重要性。
下图(a)(b)分别为预测2年到期和10年到期债券超额收益率时的各个变量重要性。(c)(d)分别为预测2年到期和10年到期债券超额收益率时,分组后各组的重要性。
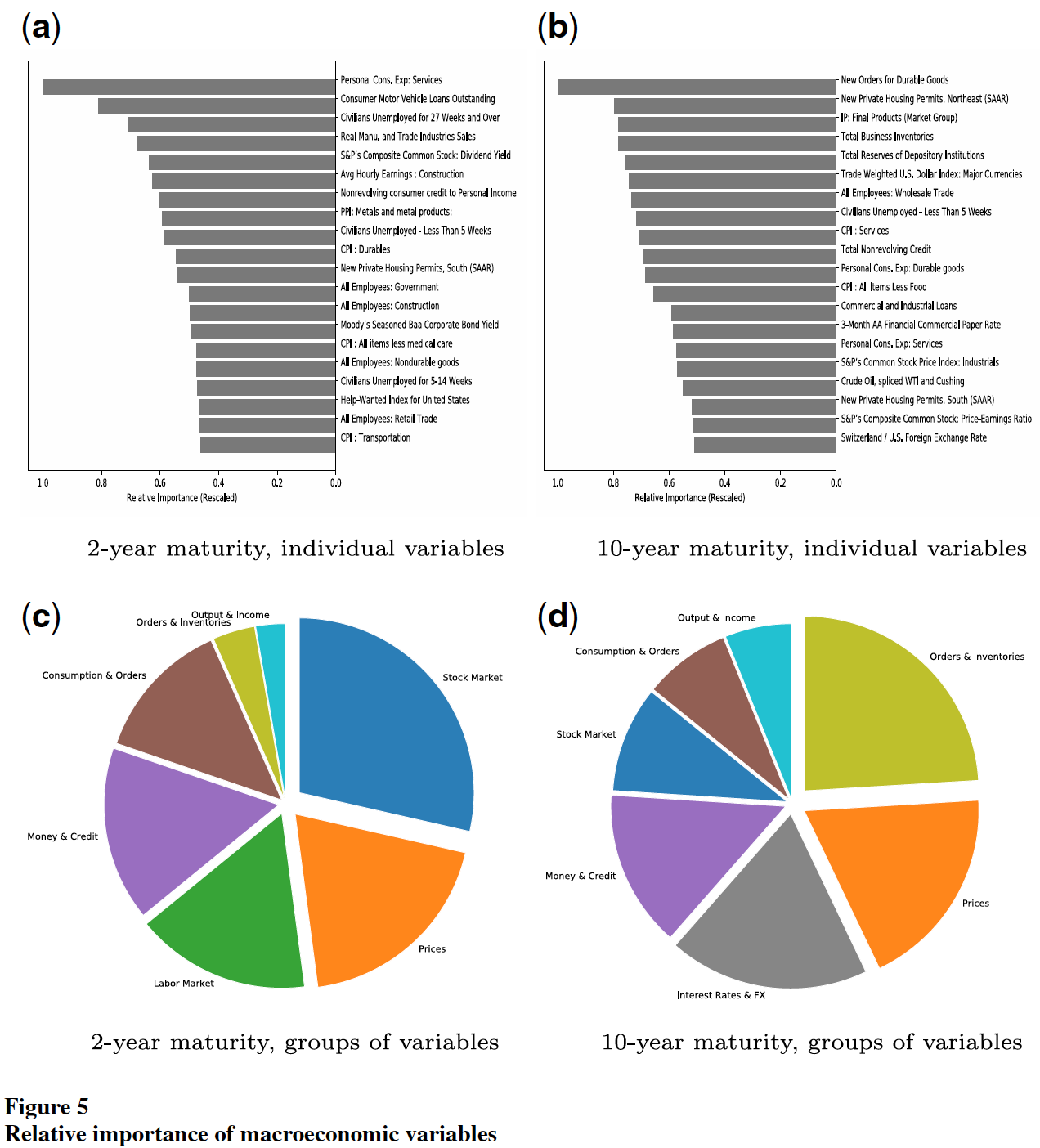
以上结果都说明非线性很重要,但能提高表现的非线性究竟是来自组间的交互,还是组内的交互?可分别对全连接网络和分组集成网络求组间二阶微分:
结果如下图:
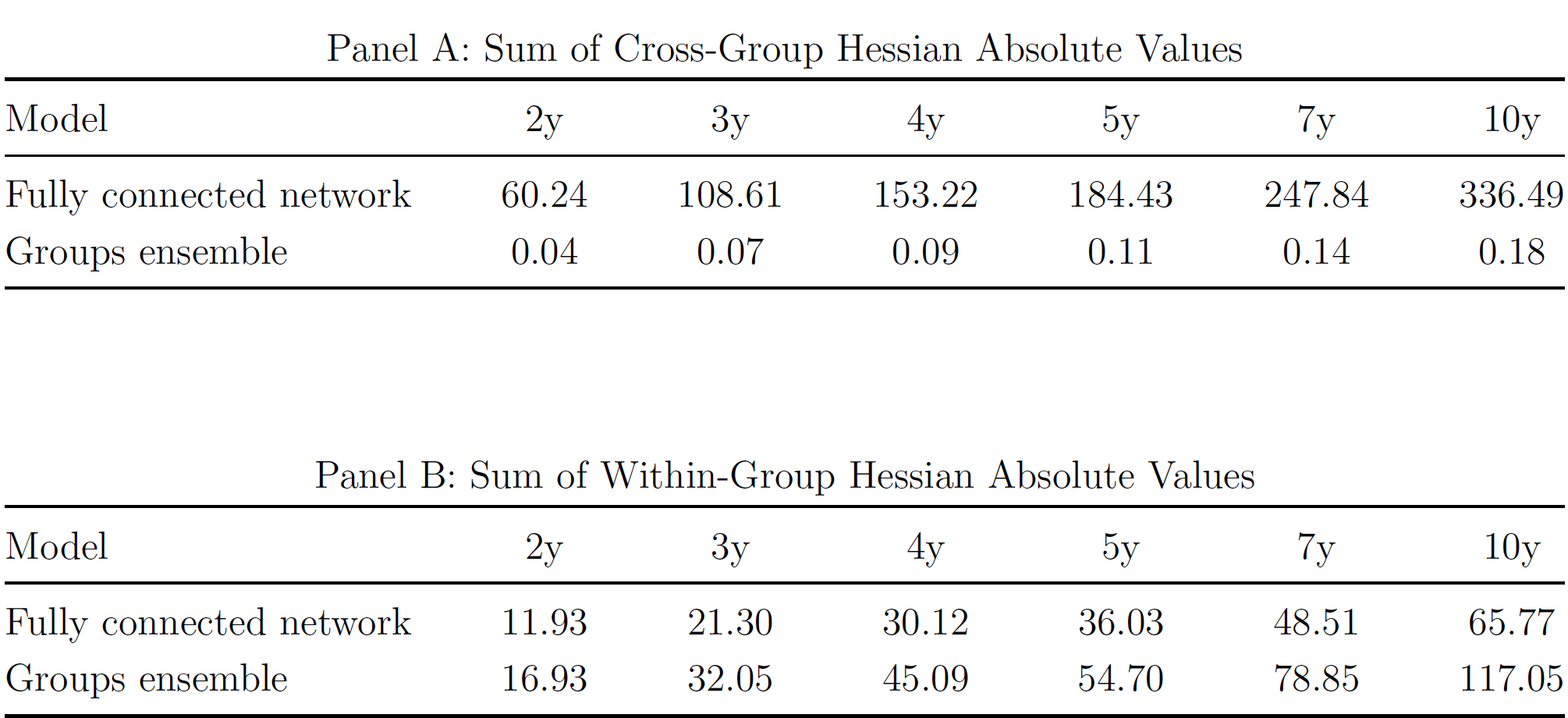
Panel A表明,全连接网络中组间交互作用很大,Panel B表明,两种神经网络中组内交互作用差不多。因此,分组集成神经网络的优异表现,来自于它禁止了组间交互作用,而允许组内交互。
4 可预测性的经济收益
可预测性能否转化为投资收益?该文考虑了单变量和多变量资产配置实验。单变量实验中,投资者只考虑投资于无风险债券和\(n\)年到期的风险债券,在文中只关注\(n=2\)或\(n=10\)的情况。在多变量情况中,投资者同时考虑到期为2-10年的债券和无风险债券。结果如下表,正的数值表明预测模型强于EH(expectation hypothesis)模型,选用的神经网络结构分别是表1和表2中最优的结构。

5 可预测性的经济驱动力
下图中,(a)(b)是画出了预测的10年到期债券收益率(实线)和美国工业产值(Industrial Production,IP)指数的增长率(虚线),(c)(d)是将虚线换成实现的10年到期债券收益率。
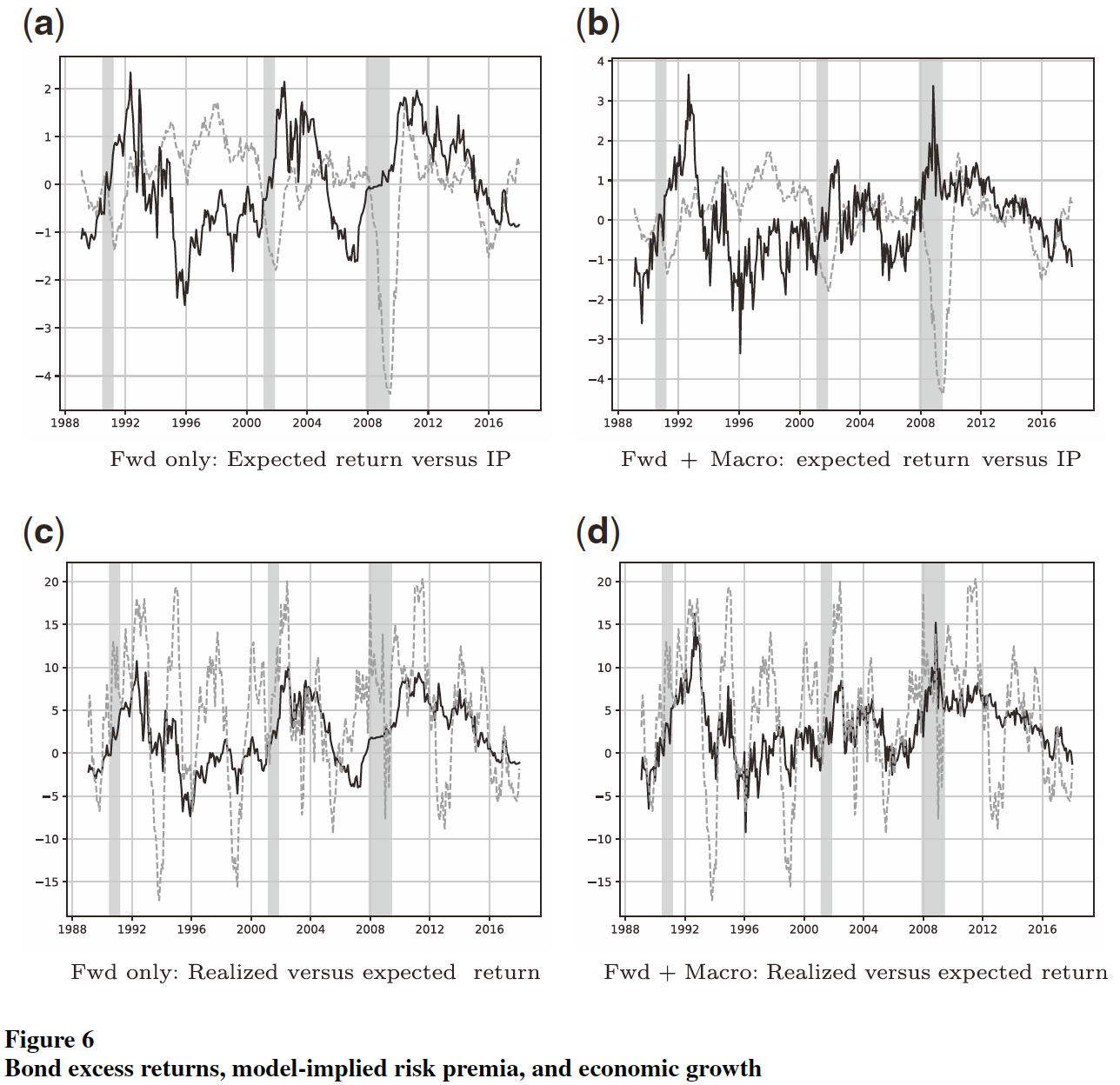
还可以计算衰退期和扩张期的夏普比率:

以上证据都表明,债券风险溢价的逆周期性很明显。
再用10年到期债券超额收益率的预测值,对一些资产定价理论中的债券风险溢价的关键驱动因子作回归。因子有:
- \(DiB(g)\)和\(DiB(\pi)\)代表了对超额收益率的信念的分歧程度,分别表示真实分歧和名义分歧,分别来自提前4季度对GDP和CPI的预测,数据来自SPF数据库。
- \(-Surplus\)是加权消费增长率的10年平均取相反数,代表风险规避,另外还用了RAbex(来自Bekaert,Engstrom和Xu,2019)作为时变的风险规避。
- \(UnC(g)\)和\(UnC(\pi)\)分别代表了经济增长和通货膨胀的不确定性。
- \({TYVIX}\)是1个月的10年到期债券风险中性隐含波动率,\(\sigma_B^{(n)}\)是10年零息债券的月内收益率变化平方和,这两个代理变量度量了债券的波动性。
结果见下表:

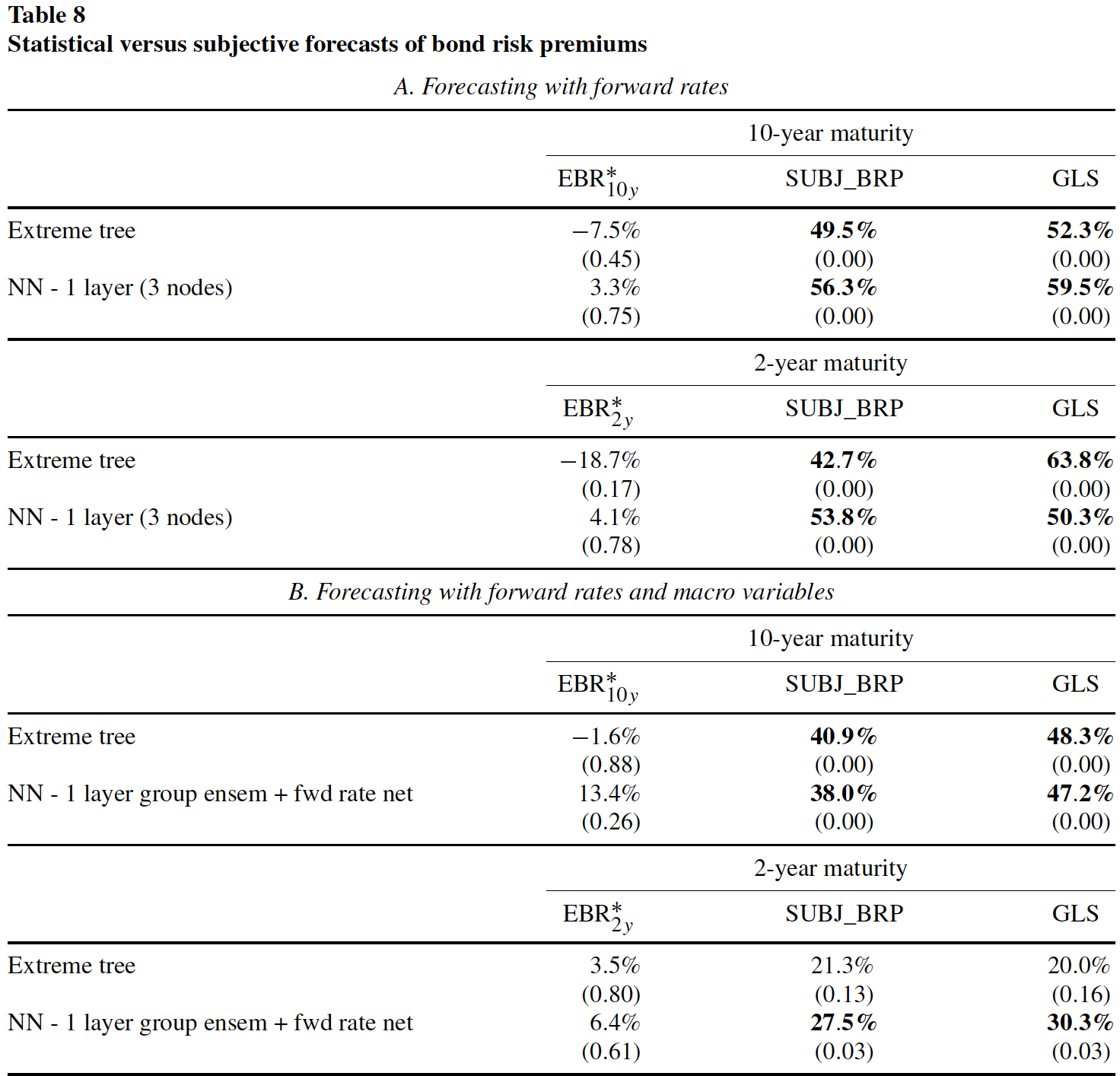
再计算10年到期债券超额收益率的预测和3个主观风险溢价代理变量(EBR*、SUBJ_BRP、GLS)的相关系数,3个变量来自Blue Chip Financial Forecasts(BCFF)的调查,相关系数见下表:
参考文献
- Bekaert, Geert, Eric C. Engstrom, and Nancy R. Xu. The time variation in risk appetite and uncertainty. No. w25673. National Bureau of Economic Research, 2019.
- Bianchi, Daniele, Matthias Büchner, and Andrea Tamoni. "Bond risk premiums with machine learning." The Review of Financial Studies (2020).
- Cochrane, John H., and Monika Piazzesi. "Bond risk premia." American Economic Review 95.1 (2005): 138-160.
- Liu, Yan, and Jing Cynthia Wu. Reconstructing the yield curve. No. w27266. National Bureau of Economic Research, 2020.
- Ludvigson, Sydney C., and Serena Ng. "Macro factors in bond risk premia." The Review of Financial Studies 22.12 (2009): 5027-5067.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号