递归--汉诺塔问题 (Hanoi)

汉诺塔问题(Hanoi)：古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上（如图）。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求输出移动的步骤 。

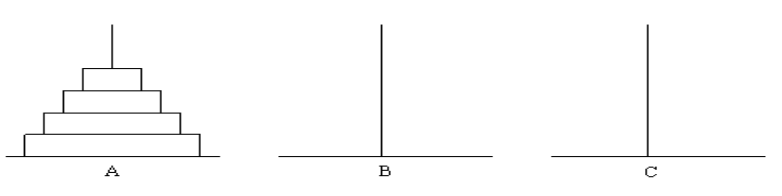
结题思路：利用递归思想结题，就是找出其每步的共同规律，然后必须有一步是递归的终止条件。

 

先假设第一种情况：3根柱，从左到右A,B,C，上面小号，底部大号，从上往下递增。

 

 

 如要完成该任务，经历3步：

1.1移至B

2.2移至C

3.1移至C

完成操作。

第二种情况：

 

 如果要完成该任务，3要移至C，也需要经历3个步骤，假设1,2是个整体，

那么第1步，1,2需要移至B柱，

      第2步，3移至C柱，

      第3步1，2移至C柱。

递归的思路：按照上述三步规则，3号盘要实现到达C柱，它会对2号盘说，接着2号盘对1号盘说，也就是这样依次调用。

如果有4个盘，那么是4调用3,3调用2,2调用1,1直接移动目标柱子（中间变化过程不一定是C柱，这里好思考一下，因为递归调用的原因，目标柱子会变化）。

递归终止的条件：当只有1个盘的情况，直接1号盘直接到达C柱，这个就是递归的终止条件。

我觉得关键是要理解，C不一定是目标柱，比如：有3个盘的时候，3号盘的目标是C，那么结果要求1，2号盘移至B柱，那么这个时候，对这样的结果而已，2号盘的目标既是B柱，C为中间柱，也就是1号盘移至C，2号盘移至B，1号盘再移回B柱，才能出现3号盘需要1,2在B柱的结果。

Python代码如下：

 

#记录第几次移动
num = 0
#把i号盘，从src柱移至to柱
def Move(i,src,to):
    #global num
    num = num + 1
    print("第 " + str(num) + " 次移动 : " + " 把 " + str(i) + " 号圆盘从 " + src + " ->移到->  " + to )

def Hanoi(n,a,b,c):
    #print(n,a,b,c)
    if (n == 1):
        return Move(1,a,c)
    else:
        #如果不好理解，可以先假设n=3来理解该递归调用
        #递归调用，n-1号盘先从a移至b
        Hanoi(n-1,a,c,b)
        #n号盘从a移至c
        Move(n,a,c)
        #n-1号盘从b移至c
        Hanoi(n-1,b,a,c)

def main():
    print("把A塔上的圆盘通过B辅助塔移动到C塔，初始A塔上序号最小的在最顶端，序号最大的在最低端！")
    n, left, mid, right = input("请输入圆盘个数和3个柱的名称，以逗号相隔：").split(",")
    n = int(n)
    Hanoi(n,left,mid,right)

if __name__ == "__main__":
    main()