数字设计基础-卡诺图的应用

目录

1 完成逻辑函数的逻辑运算2 用卡诺图记忆格雷码3 卡诺图消除组合逻辑中的冒险（毛刺）

---

1 完成逻辑函数的逻辑运算

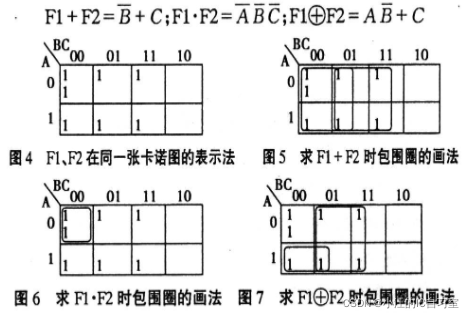
eg.已知两逻辑函数F1(A，B，C)=∑m(0，1，3)，F2(A，B，C)=∑m(0，4，5，7)，试用卡诺图分别求出F1+F2；Fl·F2和Fl+F2。

 解：

1. 将逻辑函数Fl、F2在同一张卡诺图中表示出来，将函数出现的1填在卡诺图小方格的左上角，将函数F2出现的l填在卡诺图小方格的左下角，如图4;
2. 求Fl+F2时，将Fl、F2卡诺图中出现的所有1都画入包围圈，如图5;
3. 求F1·F2时，将F1、F2卡诺图中重复出现的1画入包围圈，如图6;
4. 求F1+F2时，将F1、F2卡诺图中不重复出现的1画入包围圈，如图7;
5. 根据图5、6、7写出函数表达式：

 

 

 

2 用卡诺图记忆格雷码

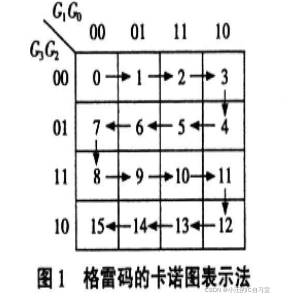
格雷码是一种常用的无权BCD码，相邻两码之间只有一位二进制数码不同。

G3 G2 为高位，G1 G0为低位：如格雷码 4 ：0110

 

 

 

3 卡诺图消除组合逻辑中的冒险（毛刺）

 

 

 

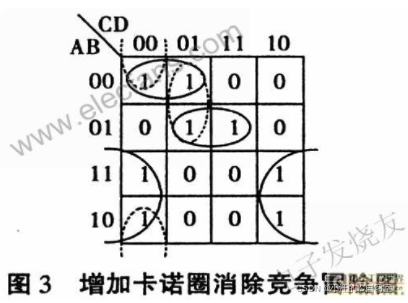
增加冗余项：

使用卡诺图判断一个组合逻辑电路是否存在着竞争冒险的一般步骤是：

1. 首先画出该电路逻辑函数的卡诺图；
2. 然后在函数卡诺图上画出与表达式中所有乘积项相对应的卡诺圈；
3. 如果图中有相切的卡诺圈，则该逻辑电路存在着竞争冒险。
4. 

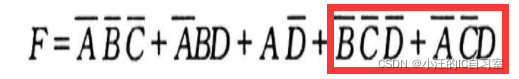
如图3所示，所谓卡诺圈相切即两个卡诺圈之间存在不被同一卡诺圈包含的相邻最小项。

如果逻辑函数的卡诺图中存在着相切的卡诺圈，该逻辑电路就存在着竞争冒险;那么，只要使函数的卡诺图中消除相切的卡诺圈，即可消除竞争冒险现象。在卡诺图上，加上一个与两相切卡诺圈相交的一个圈(一项)，破坏卡诺圈的单独相切性。加上此圈后，逻辑函数多了一个冗余项，冗余项的加入并不改变原逻辑函数的逻辑值，但冗余项的加入却可以有效地消除冒险。

 

 

 

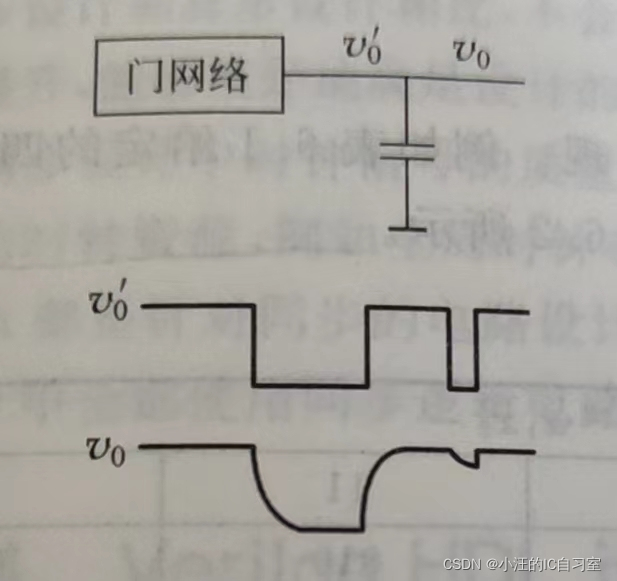
另外，组合逻辑中的毛刺除了用增加冗余项的方法来消除，还可以通过在组合逻辑的输出端增加小电容的方法来 消除，由于竞争引起的毛刺都是一些频率很高的尖脉冲信号，在电路的输出端加一个小电容，利用电容对电压的变化延迟特性来滤掉宽度极窄的毛刺信号。但是电容的加入将使得输出波形的边沿加宽，降低了电路的速度。