《数电》——化简法（公式化简法和卡诺图化简法）
最小项
定义
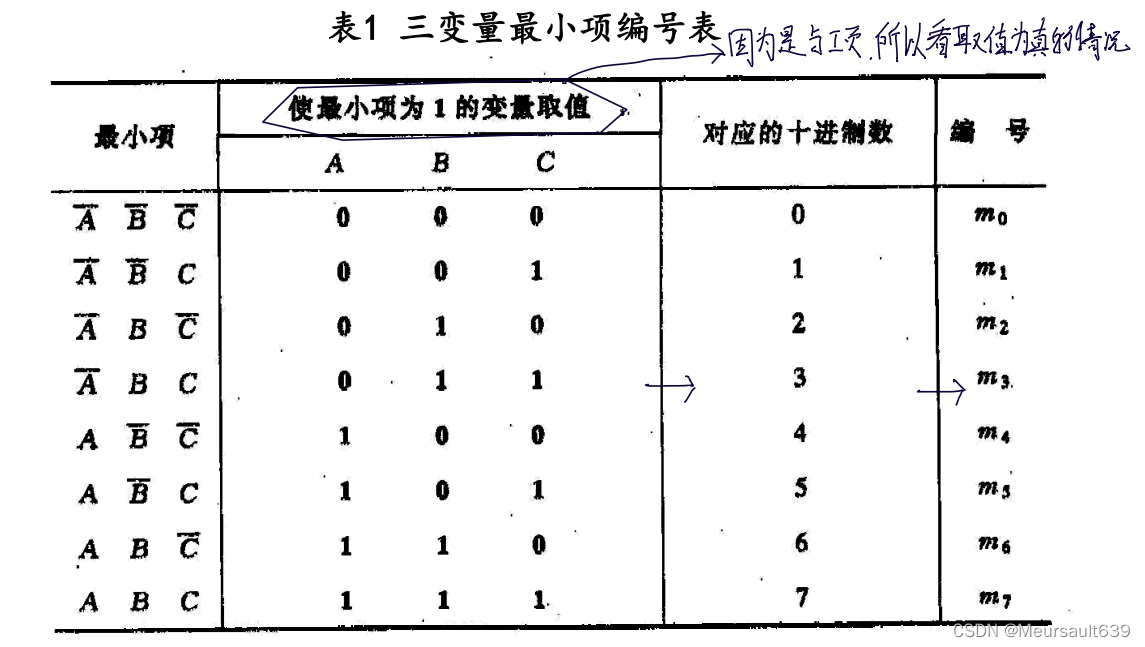
性质
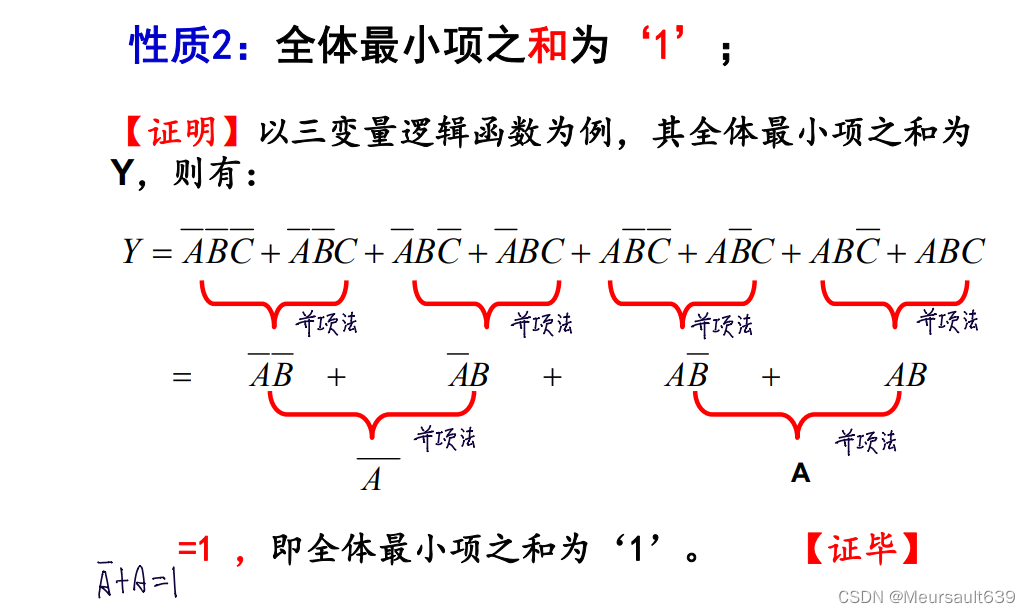
最大项
定义
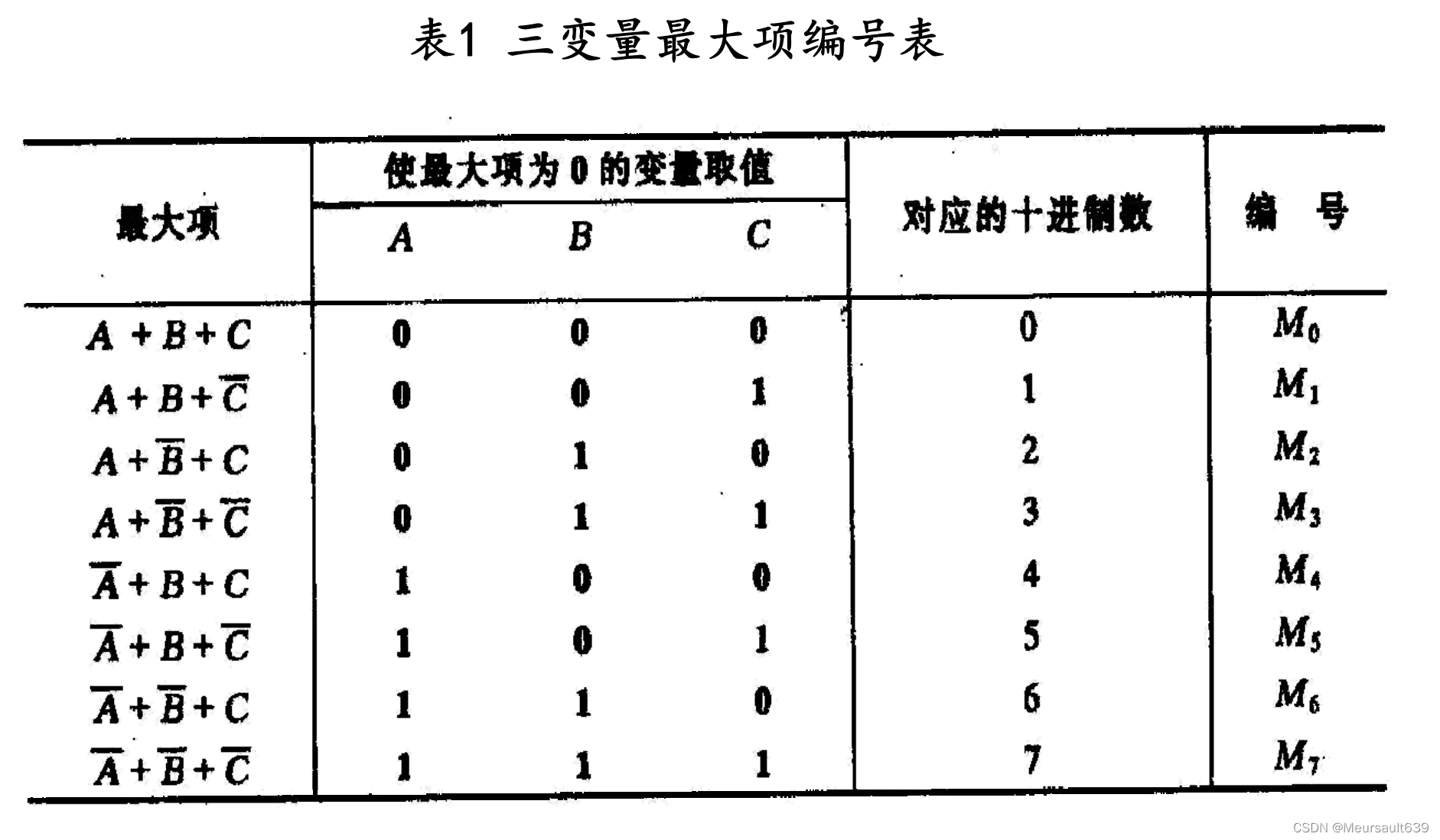
性质
两者之间的关系
其实就是互非的关系，在离散数学里也是一样的。
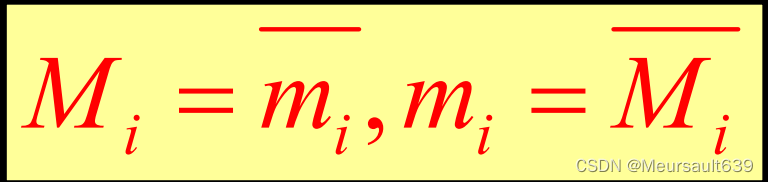
“最小项之和”形式
逻辑函数的“最小项之和”形式，也称标准 “与-或”表达式。
利用基本公式 A+ A' = 1，可将任何一个逻辑函数化为最小项之和的标准形式。这种标准形式在逻辑函数的化简以及计算机辅助分析和设计中得到了广泛的应用。
“最大项之积”形式
逻辑函数的“最大项之积”形式，也称标准“或-与”表达式。
而我们计算最大项之积的时候，通常是先计算最小项之和，再转化为最大项之积，如下所示：
卡诺图
定义
卡诺图（Karnaugh Map) —— 是由美 国工程师卡诺首先ᨀ出的一种用来᧿述逻辑 函数的特殊方格图。
★ 在这个方格图中，每个小方格代表 逻辑函数的一个最小项；
★ 且几何相邻的小方格具有逻辑相邻 性，即两相邻小方格所代表的最小项只有一 个变量取值不同。
实例
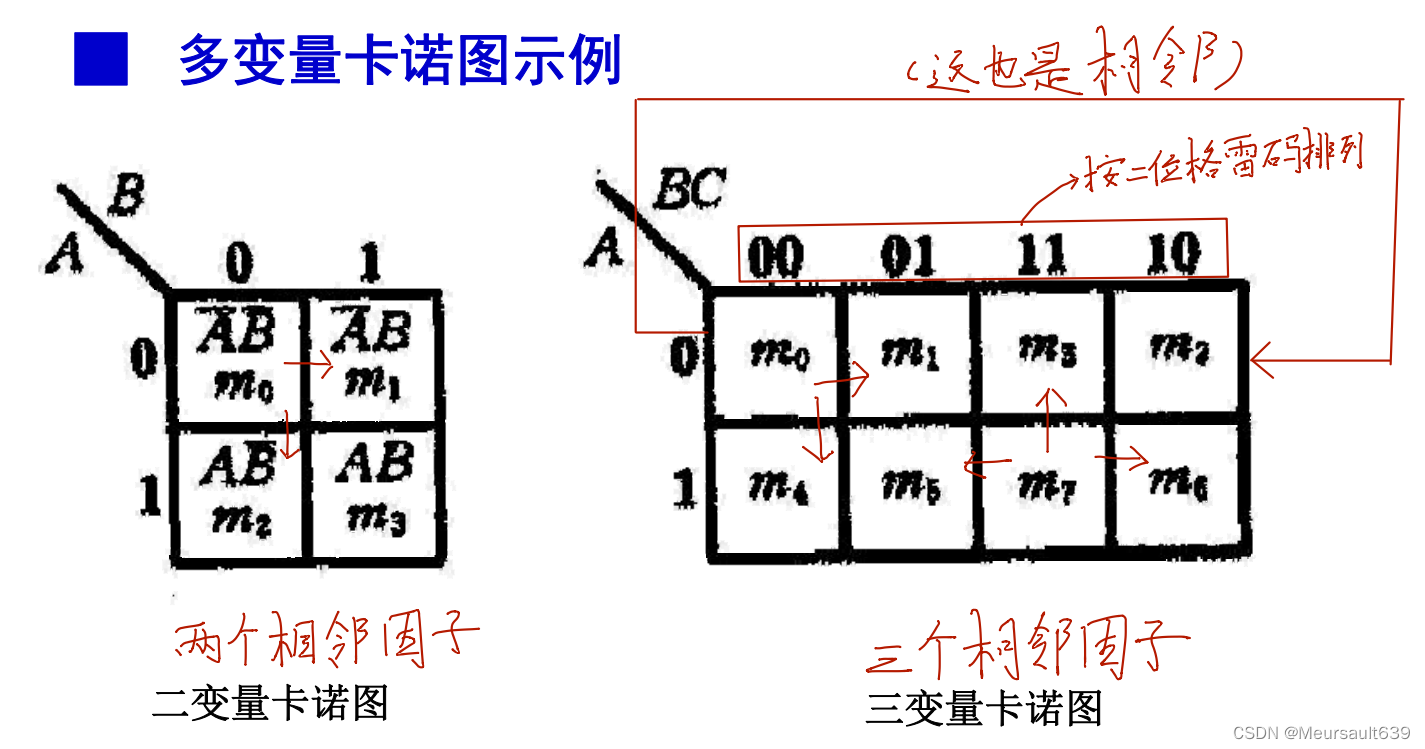
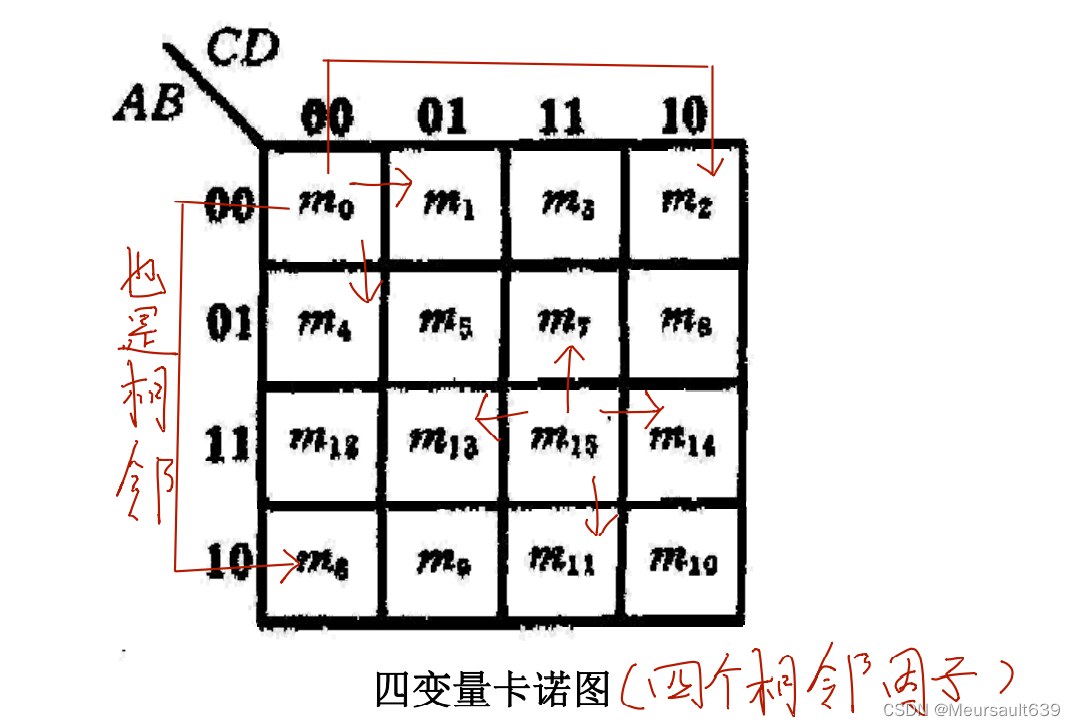
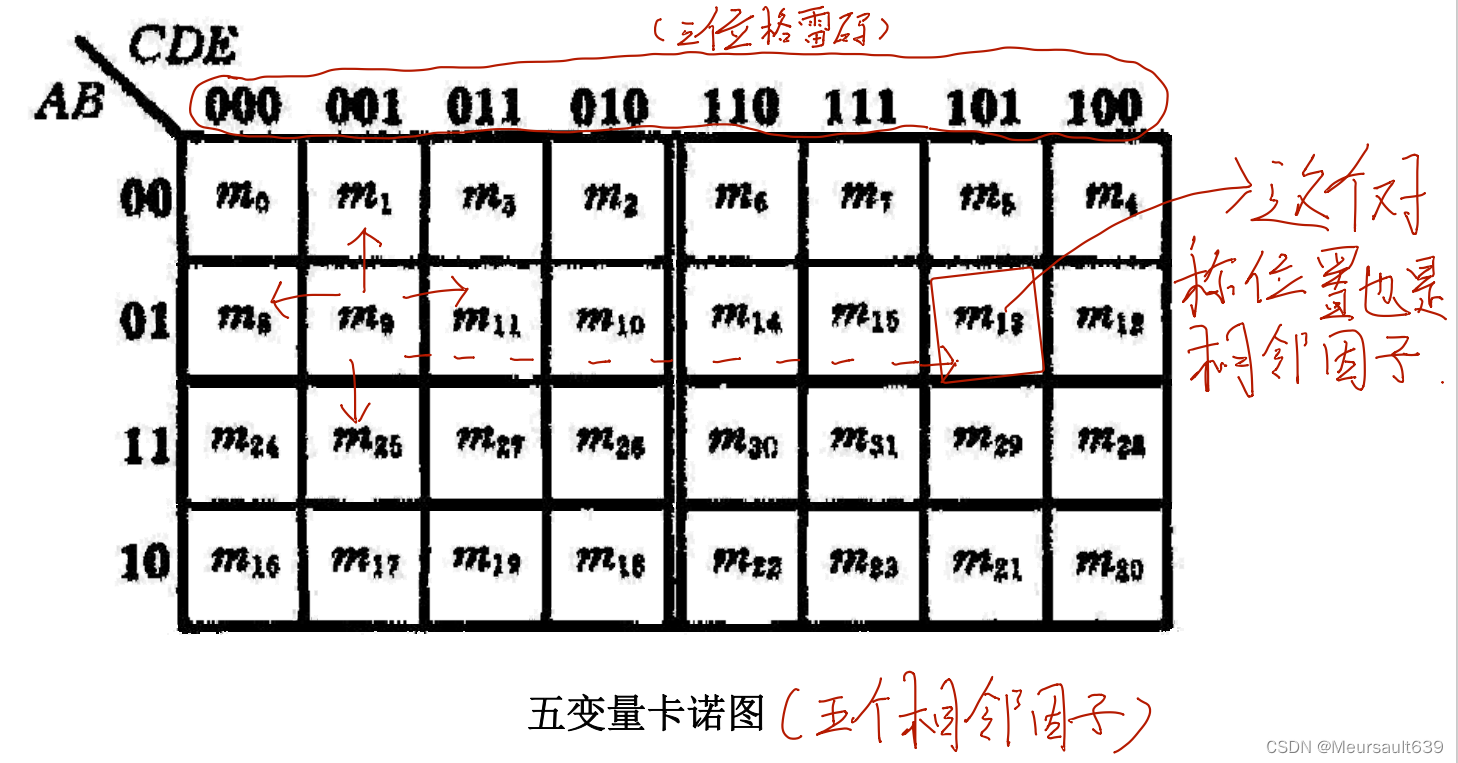特点
◆卡诺图中的小方格数等于最小项总数，若逻辑函数的变量数为 n，则小方格数为 2^n 个。
◆卡诺图行列两侧标注的0和1表示使对应方格内最小项为1的变量取值。同时，这些0和1组成的二进制数大小就是对应最小项的编号。此外，在卡诺图中，几何相邻的最小项具有逻辑相邻性，因此，变量的取值不能按照二进制数的顺序排列，必须按循环码排列。
◆卡诺图是一个上下、左右闭合的图形，即不但紧挨着的方格是相邻的，而且上下、左右相对应的方格也是相邻的。
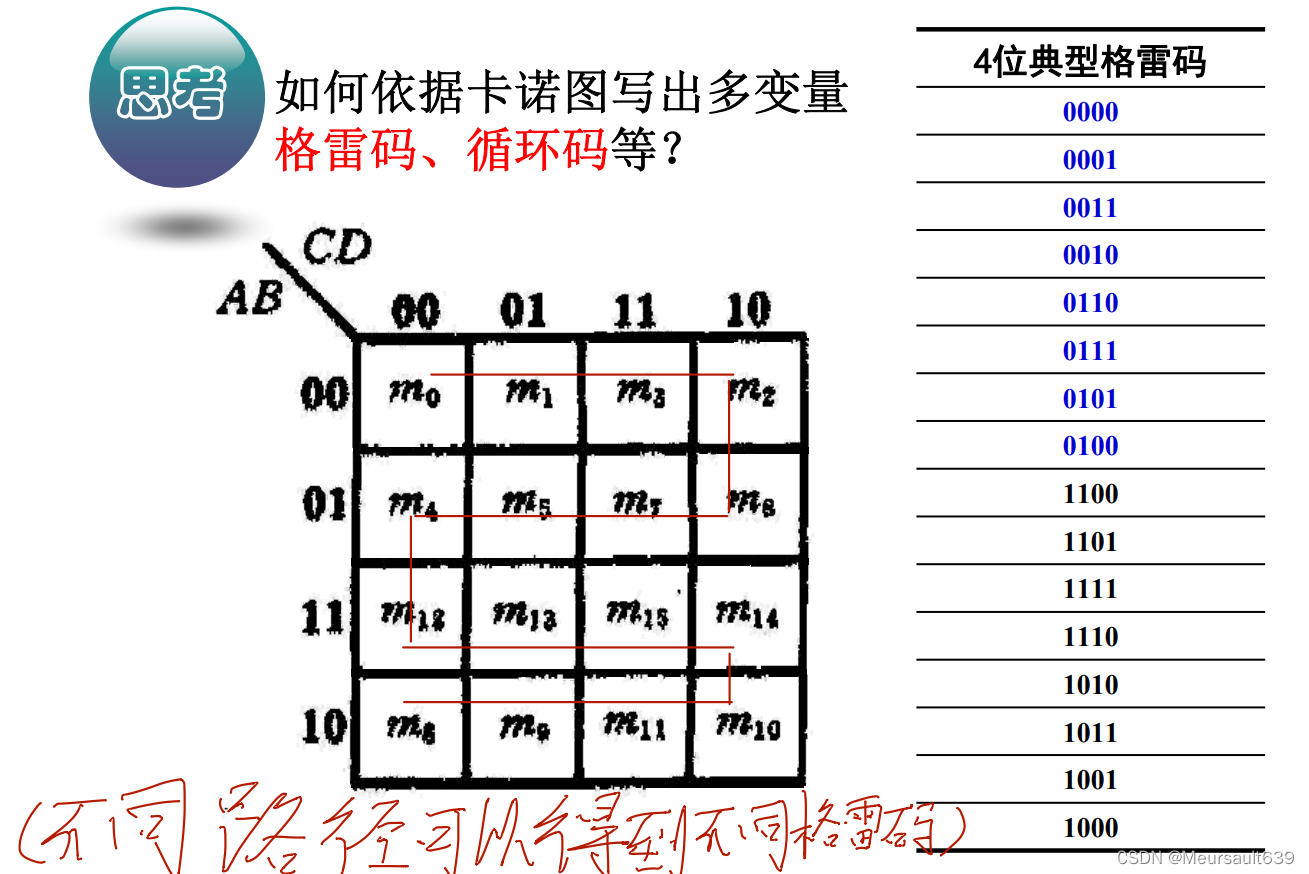
逻辑函数的卡诺图表示
画出逻辑函数的卡诺图的步骤
- 已知函数式
- 化成最小项之和形式
- 卡诺图中对应最小项格填入“1”
- 得到卡诺图
已知真值表画卡诺图
- 已知真值表
- 每组变量（即最小项）所对应的函数值
- 填入卡诺图中相应方格
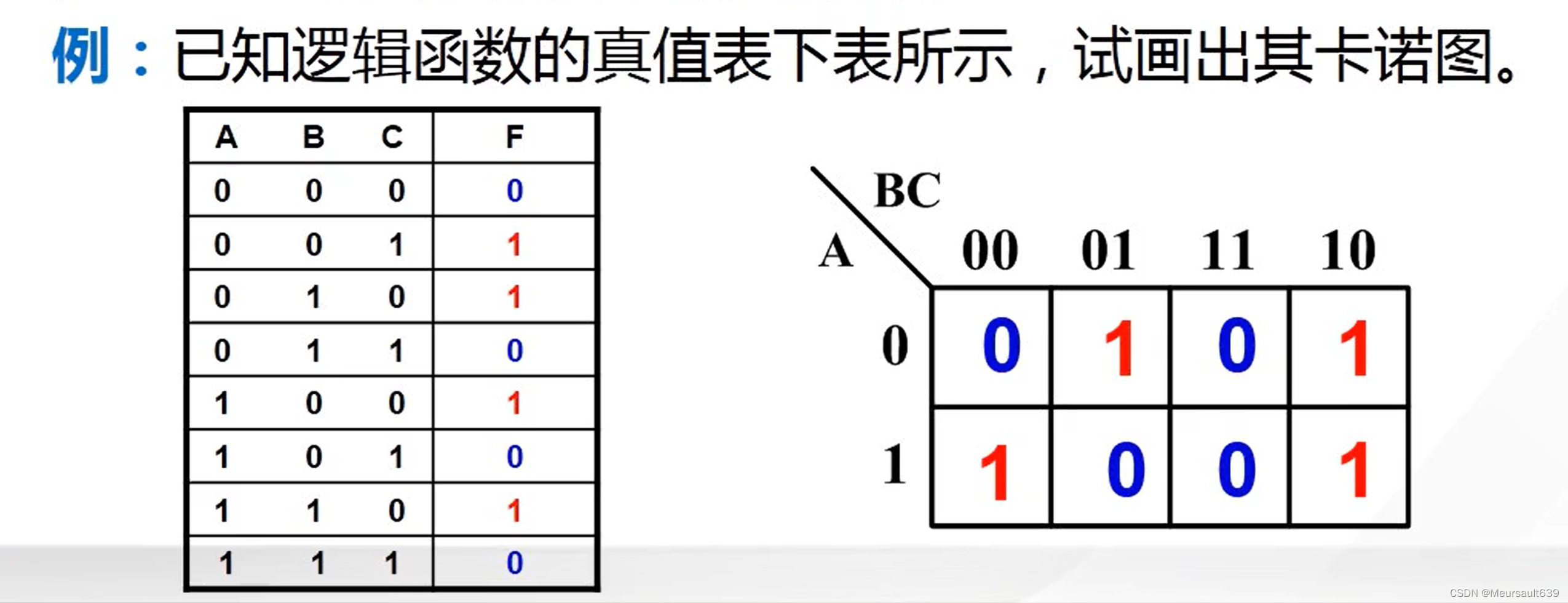
已知逻辑函数的卡诺图写表达式
- 该函数的真值表（可略）
- 写出该函数的逻辑函数式
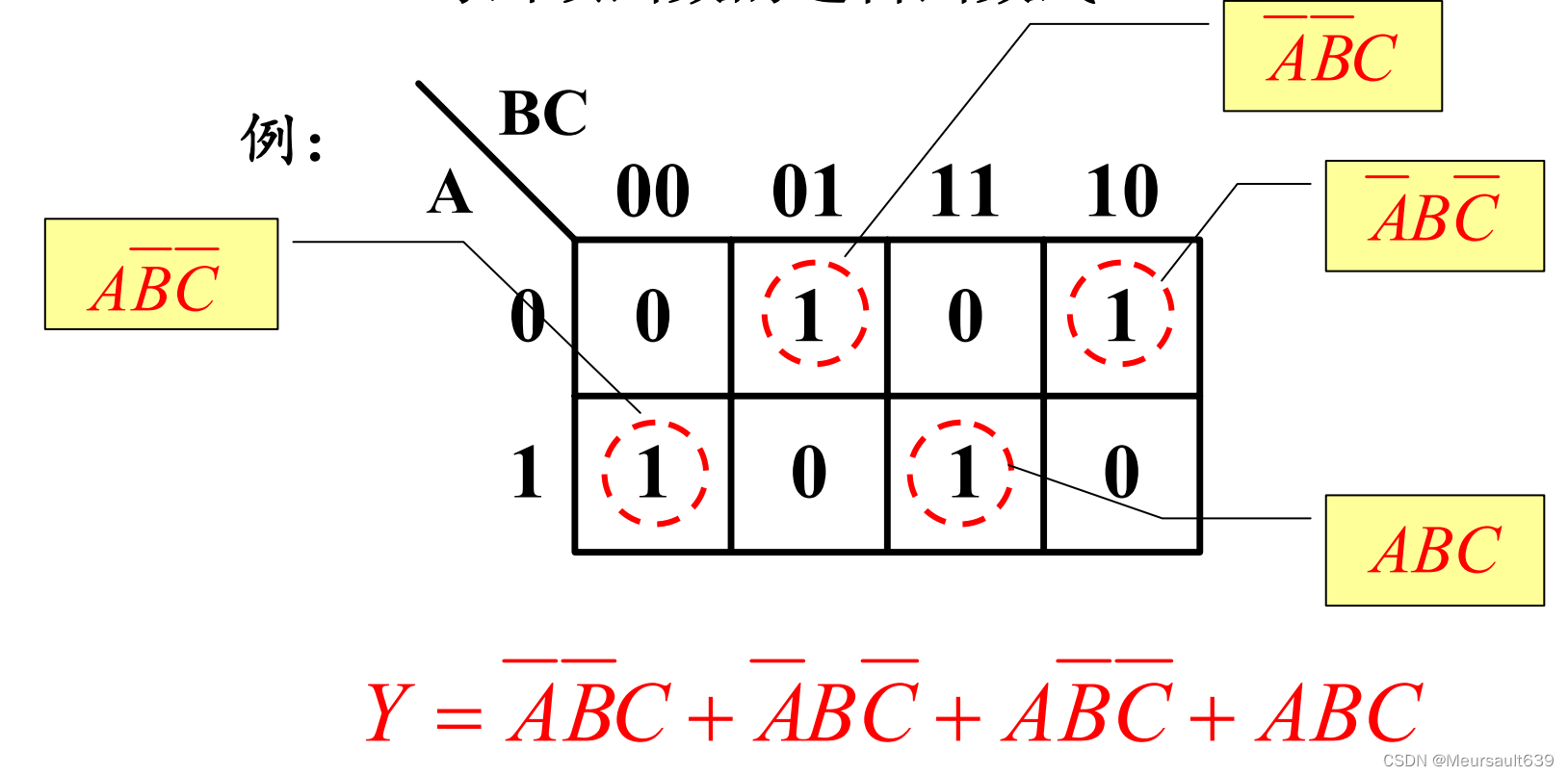
基本性质
并2消1
性质1：卡诺图中两个相邻“1”格的最小项可以合并 成一个与项，并消去一个变量。
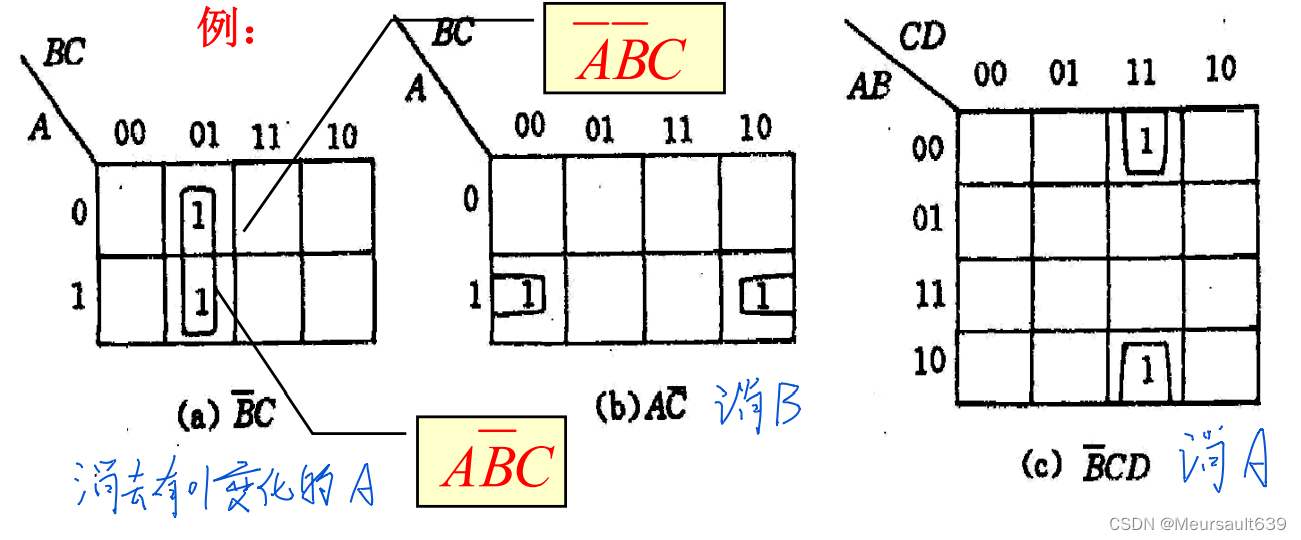
并4消2
性质2：卡诺图中四个相邻“1”格的最小项可以合并成 一个与项，并消去两个变量。
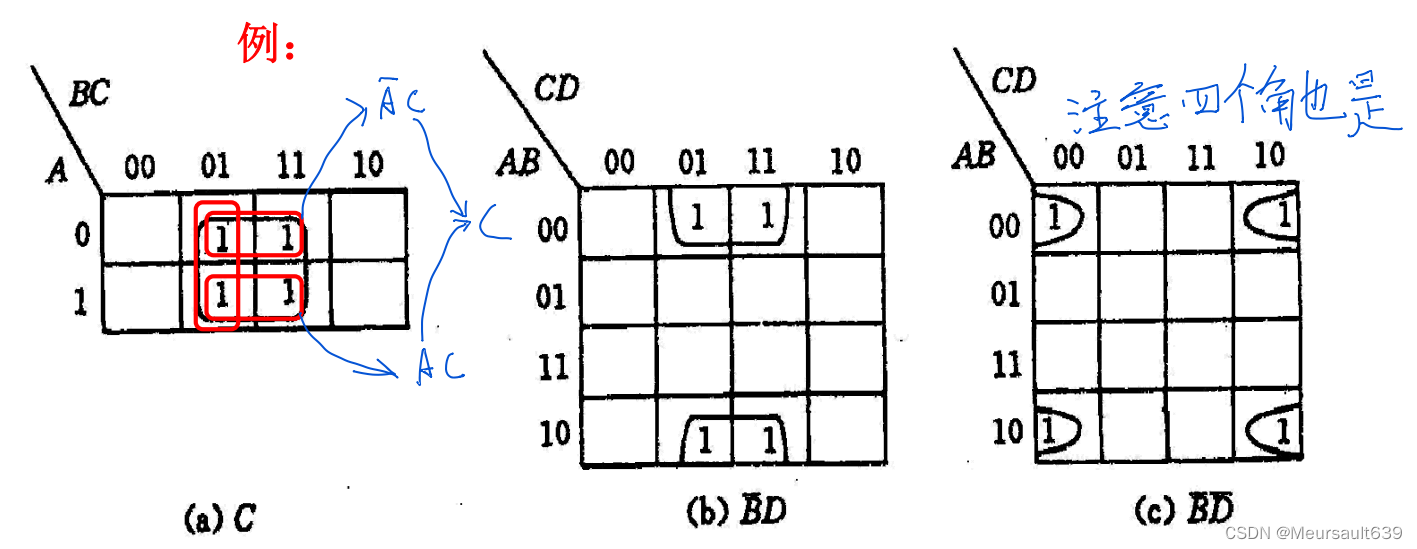
并8消3
性质3：卡诺图中八个相邻“1”格的最小项可以合并成一个与项，并消去三个变量。
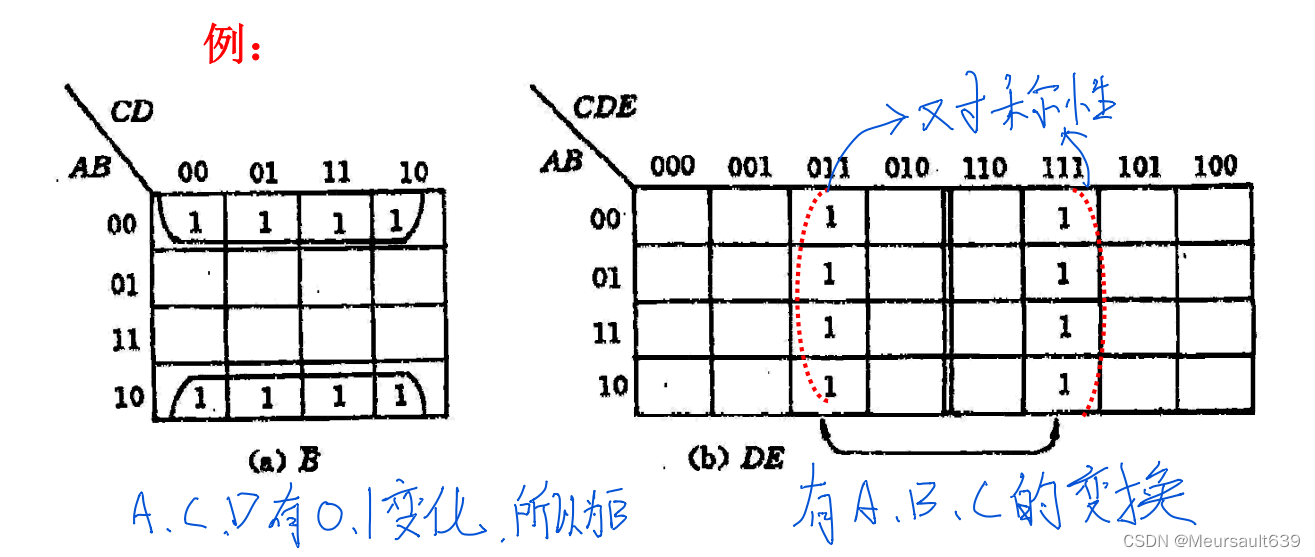
推论
在n个变量的卡诺图中，若有2^k个“1”格相邻（k=0，1，2，3，…，n），它们可以圈在一起加以合并，合并时可以消去k个不同的变量，简化为一个具有（n-k）个变量的与项。
若k=n，则合并时可消去全部变量，结果为1。因为最小项之和为1.
化简的基本步骤
- 得到函数的真值表或将函数化为最小项之和的 标准形式；
- 画出函数的卡诺图；
- 合并最小项（即“画圈”）；
“画圈”规则：
- “1”格一个也不能漏，否则表达式与函数不等；
- “1”格允许被一个以上的圈包围，因为A+A=A；
- 圈的个数应尽可能少，因为一个圈对应一个与 项，即与项最少；
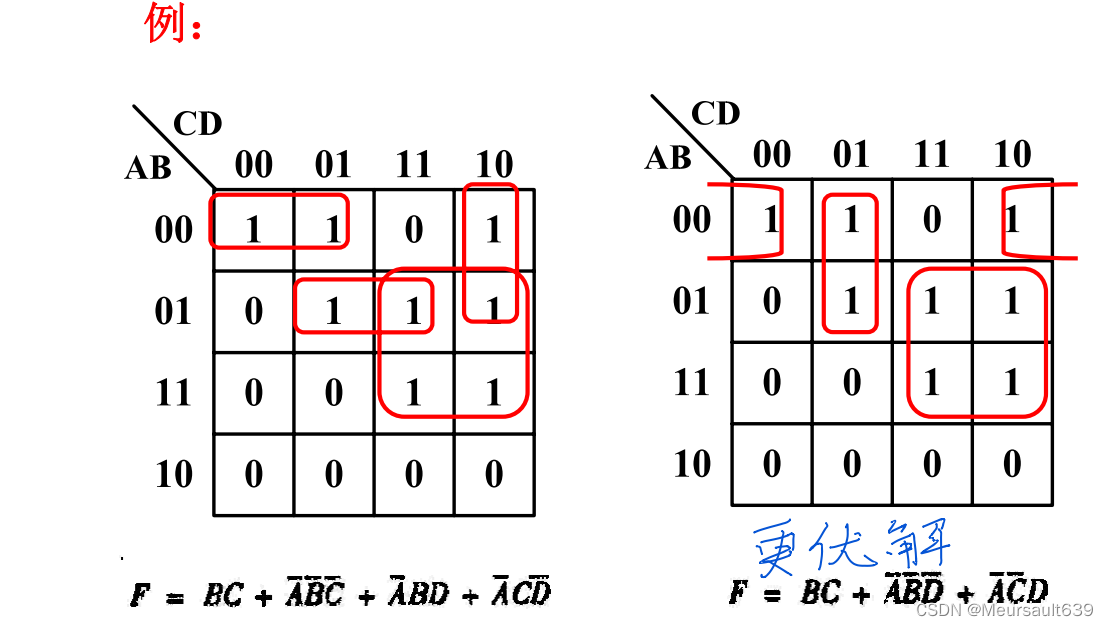
- 圈的面积越大越好，但必须为 2k 个方格。这是因为圈越大，消去的变量就越多，与项中的变 量数就越少。
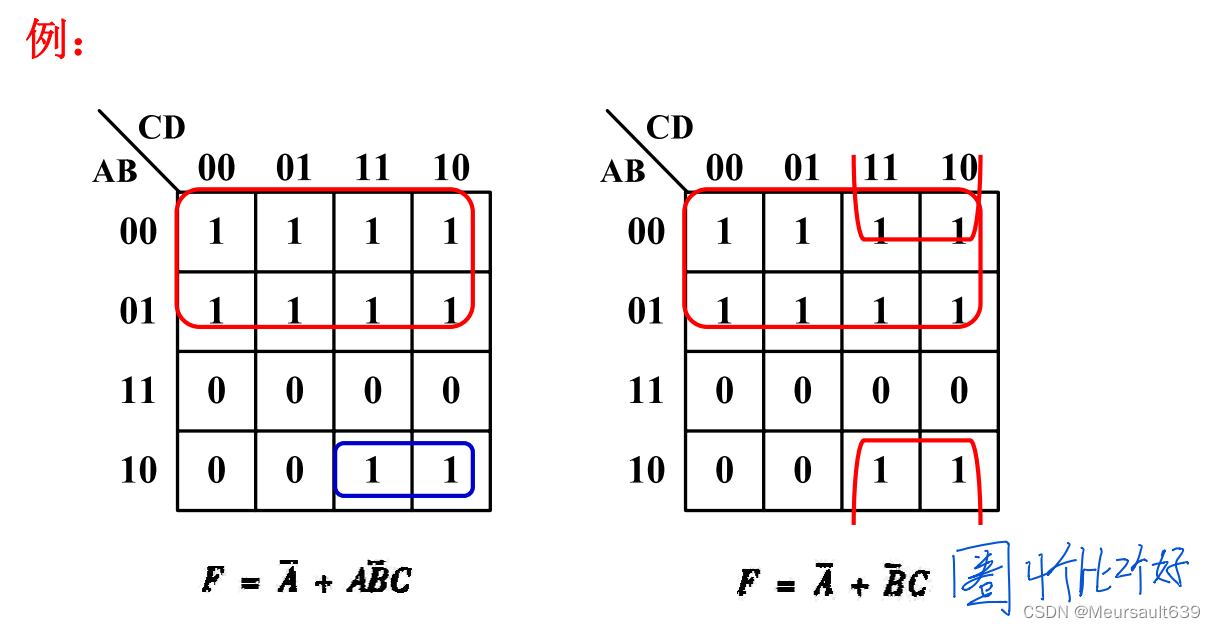
- 每个圈至少应包含一个新的“1”格，否则这个圈是多余的，即增加了冗余项；
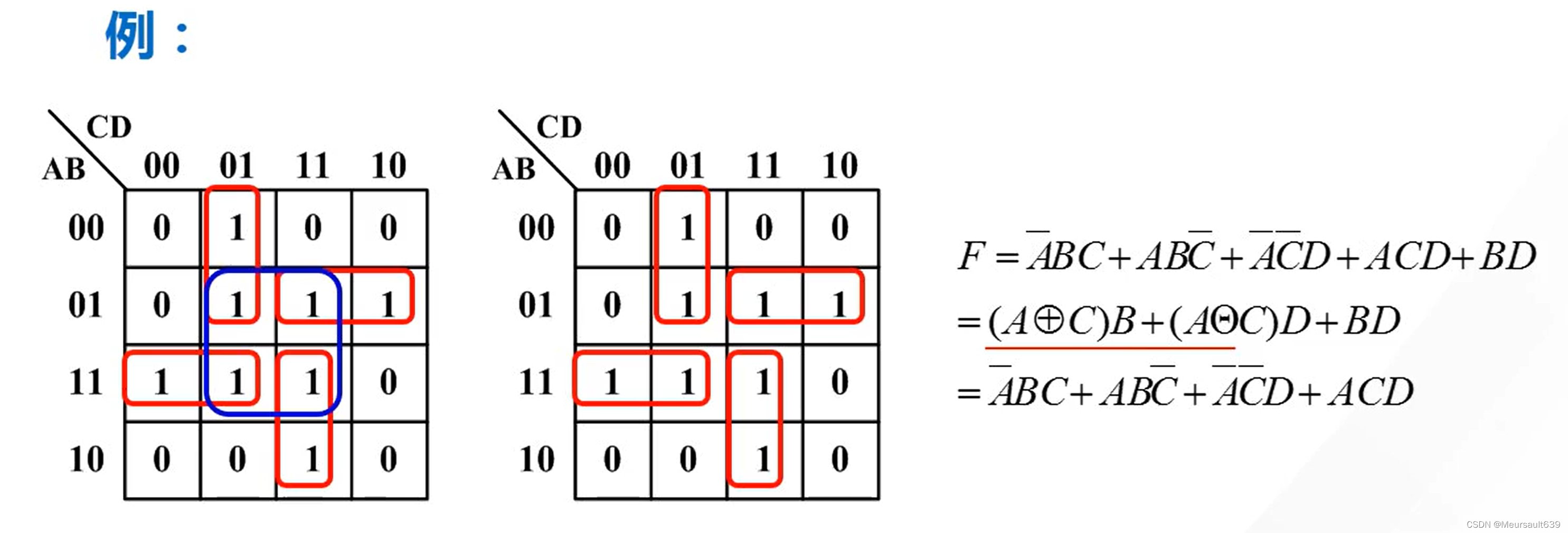
本题的BD，也就是中间那个圈是冗余的。
总规则
“可以重画，不能漏画，圈数要少，圈面要大，每个圈必有一个新‘1’” 。
示例
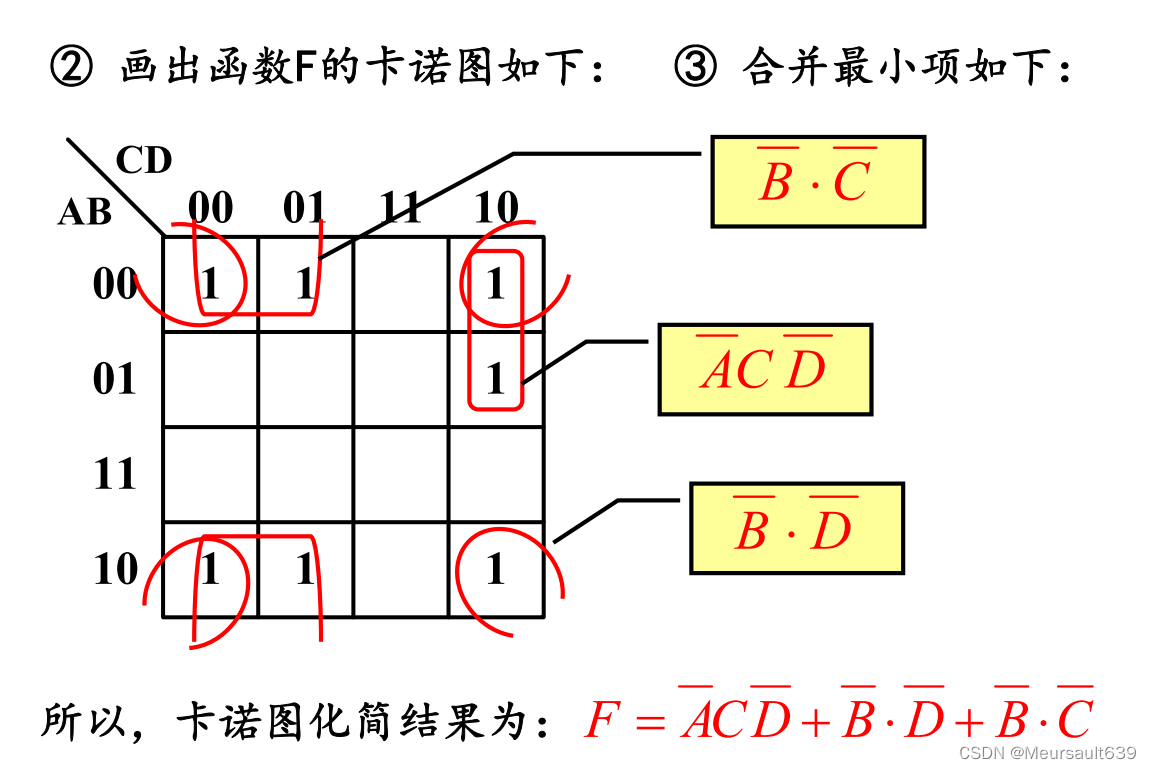
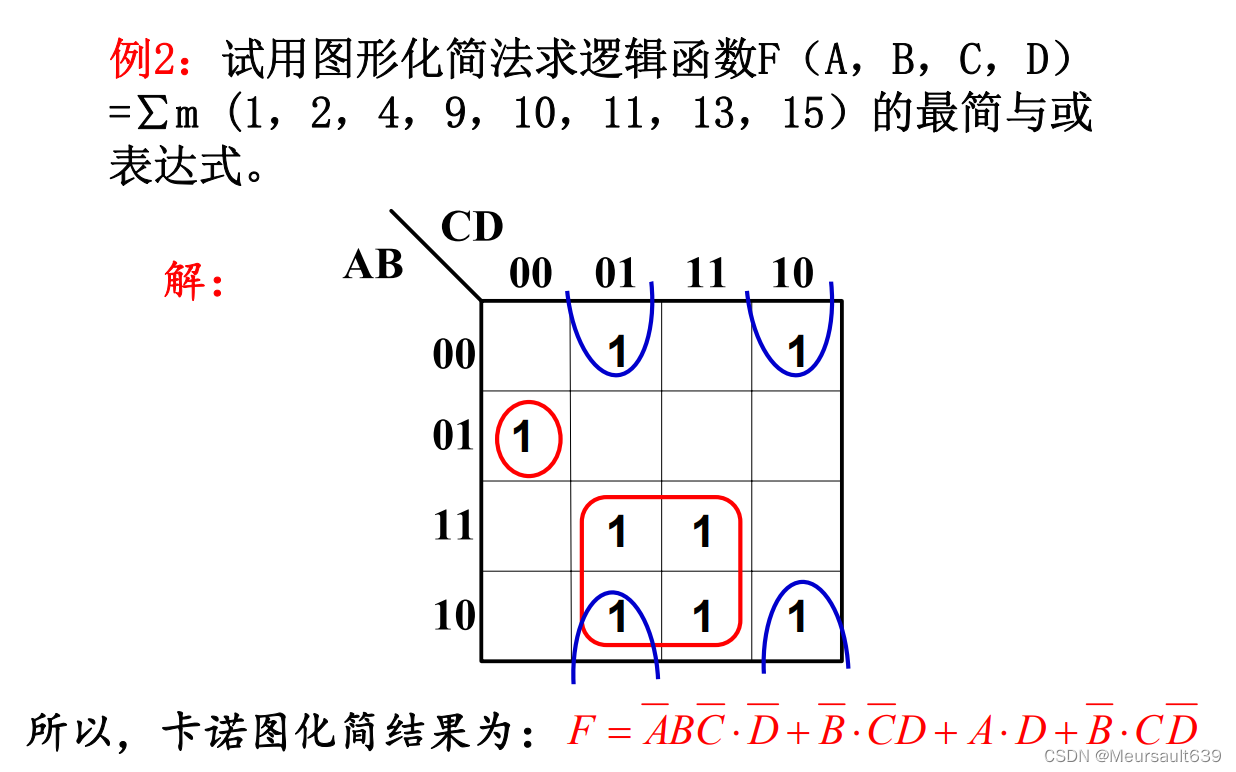
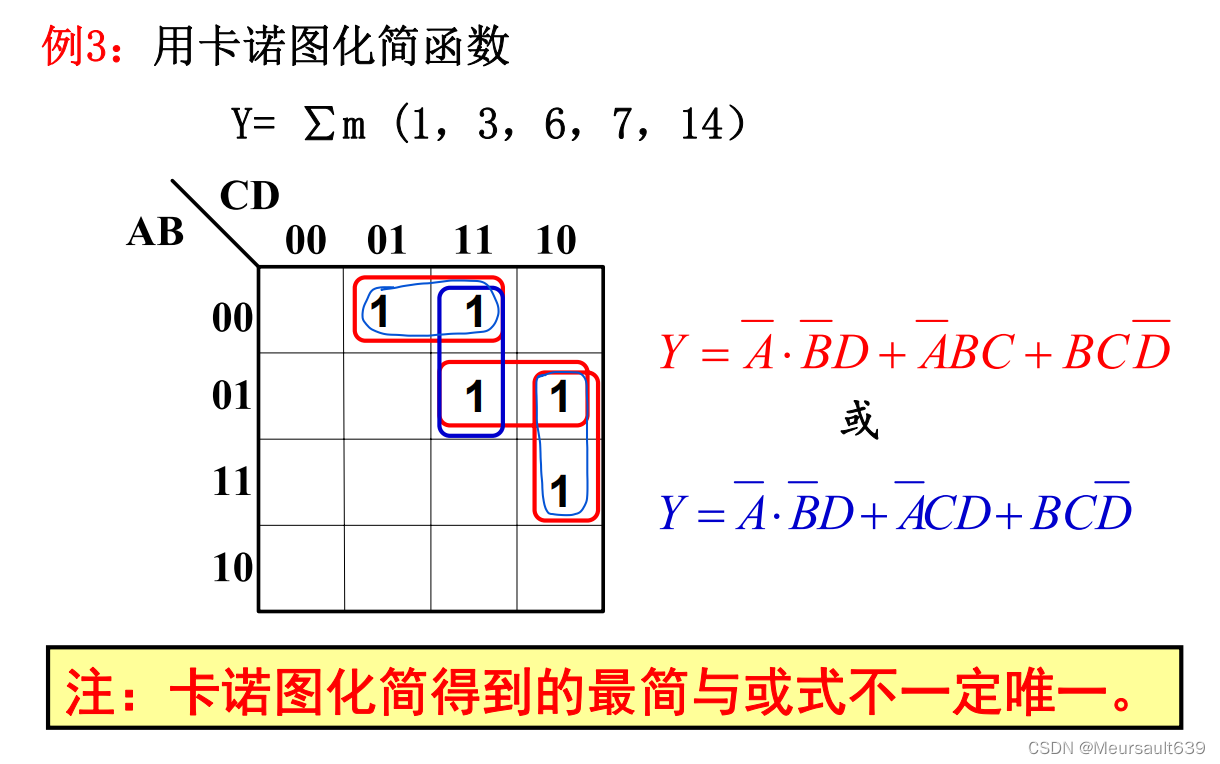
约束项
定义
约束项——在某些情况下，输入变量的取值不是任意 的。当限制某些输入变量的取值不能出现时，可以用它们 对应的最小项恒等于0来表示。这些恒等于0的最小项叫约 束项。
任意项
定义
任意项——有时输入变量的某些取值是1还是 0皆可，并不影响电路的功能。在这些变量取值 下，其值等于1的那些最小项称为任意项。
无关项
定义
无关项——约束项和任意项统称为逻辑函数中的无关项。“无关”指是否将这些最小项写入逻辑函数式无关紧要，在卡诺图中用“×”表示无关项。在化简逻辑函数时，可认为它是1，也可认为它是0。
应用
化简具有无关项的逻辑函数时，如果能合理利用这些 无关项，一般都可以得到更加简单的化简结果。
合并最小项时，究竟把卡诺图上的“×”作为1还是0， 应以得到的相邻最小项矩形组合最大，而且矩形组合数目 最小为原则。
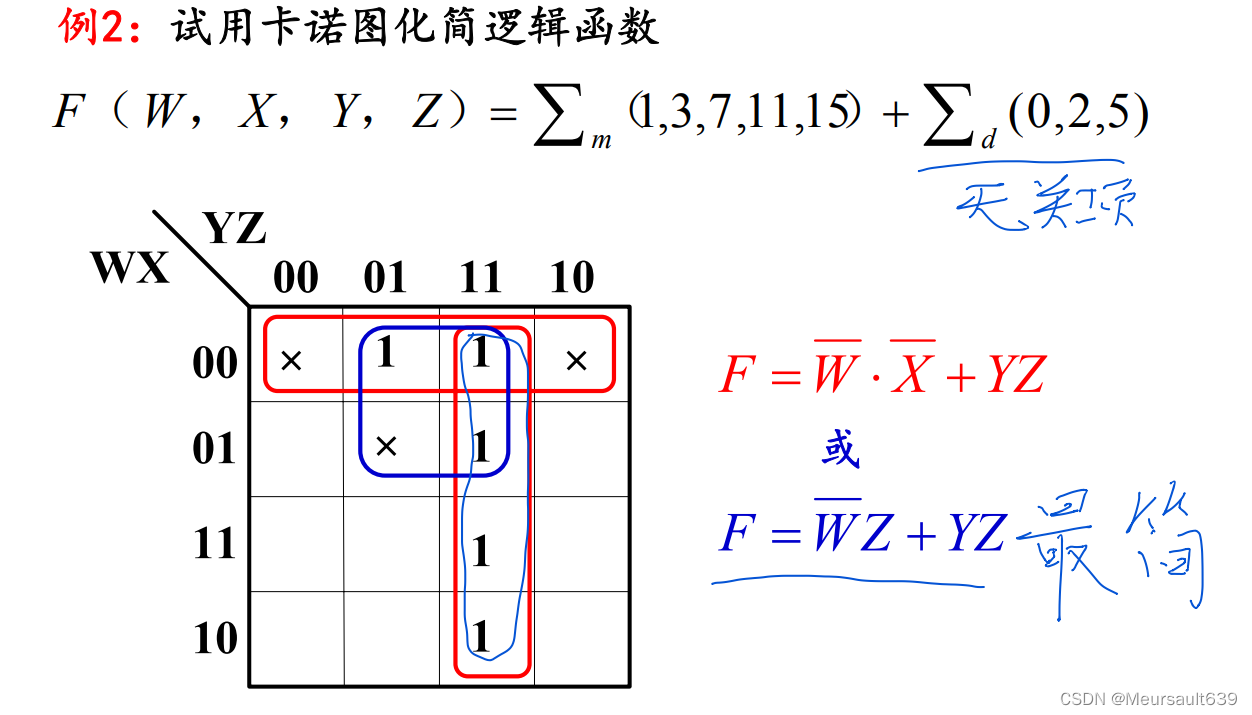
此例有两种解法，从原理而言，两 种解法均正确，但就“最简”原则而言，只有一 种解法最简单、最可取。因此，在考虑卡诺图 化简不唯一性的同时，还应考虑“最简”原则。
转自：https://blog.csdn.net/weixin_66578482/article/details/125931372
